10.3. Середньозважені індекси

Агрегатний індекс є простим для проведення самих розрахунків. Але на практиці існують ситуації, коли цю форму загального індексу використати неможливо.

Вибір тієї чи іншої форми залежить від мети, з якою він визначається і вихідних даних.

Іншою формою існування загальних індексів є середньозважені індекси. Ця форма пов’язана з перетворенням агрегатного індексу в середньоарифметичний або середньогармонійний індекси.

Середньозважені індекси повинні бути тотожні агрегатному. Отже, вага середньоарифметичного і середньогармонійного індексів повинні визначатися на основі дотримання умов тотожностей. Якщо треба охарактеризувати зміну екстенсивного показника в середньому по сукупності різнорідних елементів, використовують середньоарифметичний зважений індекс.

Розглянемо перетворення агрегатного індексу в середньоарифметичний на прикладі індексу фізичного обсягу

, коли , то(10.12)

Замінивши значення чисельника q₁ на i_qq₀, маємо формулу середньоарифметичного індексу:

, (10.13)

де ― вага;

і_q ― індивідуальний індекс.

Правило тотожності: середньоарифметичний індекс тоді буде тотожний агрегатному і давати такий же результат, коли вагою індивідуального індексу будуть взяті складові знаменника агрегатного індексу.

Середньозважений загальний індекс інтенсивного показника обчислюють за формулою середньогармонійного індексу.

Розглянемо перетворення агрегатного індексу в середньогармонійний на

40

прикладі індексу цін:

, коли , то(10.14)

Замінивши значення знаменника р₀ на , маємо формулу середньогармонійного індексу:

, (10.15)

де ― вага.

Правило тотожності: середньогармонійний індекс тоді буде тотожний агрегатному і давати такий же результат, коли вагою індивідуального індексу будуть взяті складові чисельника агрегатного індексу.

10.4. Індекси зі змінною і постійною вагою

При вивченні складних суспільних явищ більше ніж за два періоди застосовують ряди індексів за ланцюговою і базисною системами. Вибір системи залежить від мети дослідження. Вирішуючи проблему вибору ваги чи вимірника, треба дотримуватися правила: індекси інтенсивних (якісних) показників визначають зі змінною вагою, а індекси екстенсивних (кількісних) показників ― з постійними вимірниками.

1. Індексний ряд екстенсивного показника з:

а) постійними вимірниками:

; ;;;

б) змінними вимірниками:

; ;;

2. Індексний ряд інтенсивного показника з:

а) змінною вагою:

; ;;;

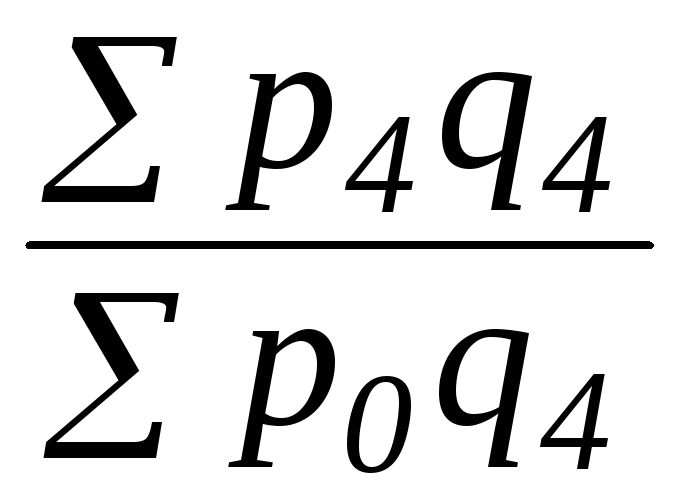б) постійною вагою:

; ;;

При обчисленні загальних індексів з постійною вагою (чи вимірниками) діє взаємозв’язок: добуток ланцюгових індексів дорівнює кінцевому базисному. На загальні індекси зі змінною вагою чи вимірниками ці правила не поширюються.

10.5. Індекси змінного та фіксованого складу. Індекси структурних зрушень

41

У статистичному аналізі особливу групу становлять індекси середніх величин. Зміна середнього рівня інтенсивного показника обумовлена впливом тих факторів, від яких залежить сама середня величина.

Аналіз динаміки середнього рівня здійснюють на основі побудови системи взаємозалежних індексів. Індекс, що характеризує зміну середнього рівня інтенсивного показника за рахунок зміни всіх факторів у цілому, дорівнює добутку індексів-співмножників, кожний з яких характеризує зміну лише одного фактора, і тим самим вплив цієї зміни на динаміку середньої величини.

Індекс змінного складу являє собою відношення середніх рівнів інтенсивного показника за поточний і базисний періоди.

Розглянемо цю групу індексів на прикладі розрахунку середньої ціни:

―середня ціна продукції в поточному періоді; (10.16)

―середня ціна продукції в базисному періоді (10.17)

Тоді

, (10.18)

де р₁, р₀ ― рівні осередненого показника;

q ₁, q₀― вага інтенсивного показника.

Величина цього індексу залежить як від зміни кожної одиниці продукції, так і від зміни кількості виробленої продукції.

Індекс фіксованого складувизначає зміну середнього рівня інтенсивного показника за рахунок тільки зміни цін на кожну одиницю продукції:

(10.19)

Індекс структурних зрушень визначає зміну середнього рівня інтенсивного показника тільки за рахунок змін у розмірі виробленої продукції:

(10.20)

Взаємозв’язок показників:

(10.21)

Кожний із індексів ― співмножників оцінює ступінь впливу відповідного фактора на середній рівень інтенсивного показника.

Контрольні запитання

1. Що є індексом в статистиці?

2. Що характеризують індивідуальні індекси? Наведіть приклади.

3. У чому сутність загальних індексів?

4. Правило побудови загальних індексів поясніть на прикладі індексів товарообігу.

5. Коли виникає необхідність перетворення агрегатного індексу в се-

42

редньоарифметичний або середньогармонійний?

6. Що є індексом змінного складу, як він розраховується та що характеризує?

7. Що є індексом постійного складу, як він розраховується?

8. Яка залежність між індексами змінного, постійного складу та структурних зрушень?

9. Як визначити питому вагу впливу різних факторів на зміну результативного показника в абсолютних величинах?