4.3 Суть і використання середніх величин

В економічному аналізі дуже часто треба мати показник, який здатний відобразити характерний рівень ознаки, притаманної усім елементам сукупності. Таким показником є середня величина.

Середня ― це узагальнений показник, який характеризує типові розміри варіюючої ознаки, якісно однорідних суспільних явищ в конкретних умовах місця і часу.

Середня характеризує типовий рівень варіюючої ознаки. Вона відображає те спільне, що об’єднує всю статистичну сукупність.

Умови застосування середньої величини:

• згідно з дією закону великих чисел, середня проявляє себе лише у випадку узагальнення масових фактів;

• статистична сукупність повинна бути якісно однорідною;

• повинна мати місце різниця індивідуальних значень ознаки.

4.4 Види середніх величин та методи їх розрахунку

Середня величина лише тоді може бути узагальнюючою характеристикою, коли при зміні всіх варіант загальний обсяг варіюючою ознаки залишиться незмінним. Тобто, вид середньої вибирають залежно від того, що являє собою загальний обсяг варіюючої ознаки.

В статистиці поширено використання середніх:

• арифметичної;

• гармонійної;

• хронологічної;

• геометричної;

• квадратичної.

Середня арифметична ― один із найбільш поширених видів середньої величини.

Середня арифметична буває:

• простою;

• зваженою.

Середня арифметична проста використовується тоді, коли розрахунок здійснюється на основі не згрупованих даних, коли всі варіанти ознаки повторюються по разу, або однакову кількість разів.

Наприклад, визначити середній заробіток майстерні, коли Іванов М.І. заробив 155 грн., Чумак В.В. ― 170 грн., Дорошенко І.В. ― 140 грн.

Розрахунок середньої арифметичної простої здійснюється як:

, (4.1)

де х ― значення ознаки (варіанти);

n― кількість одиниць.

16

Тоді середній розмір заробітної плати по майстерні складе:

грн.

Коли має місце розрахунок середньої на основі згрупованих даних, передусім варіаційного ряду розподілу, використовують формулу середньої арифметичної зваженої. У цьому випадку для визначення загального обсягу варіюючої ознаки слід кожну з варіант помножити на частоту і отримані результати підсумувати.

Формула розрахунку середньої арифметичної зваженої:

, (4.2)

де f ― частота повторюваності ознаки.

Використовуючи властивості середньої арифметичної, розглядають спрощений спосіб визначення середньої арифметичної ― спосіб “моментів”:

, (4.3)

де m₁ ― момент першого порядку;

;

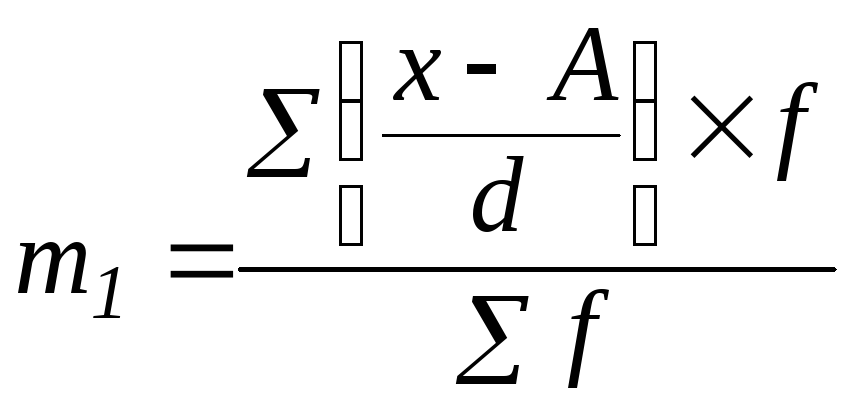d ― ширина інтервалу;

А ― значення ознаки, яке знаходиться в середині ряду розподілу і має найбільшу частоту.

Середня гармонійна буває:

• простою;

• зваженою.

Якщо підсумовуванню підлягають не самі варіанти, а обернені їм числа, то треба використовувати середню гармонійну просту:

(4.4)

Приклад. На виготовлення одиниці продукції один робітник витрачає 40 хвилин, другий ― 48. Визначити середні витрати часу на виготовлення одиниці продукції.

хвил.

Таким чином, на виготовлення однієї деталі в середньому витрачається 43,6 хвилин.

Якщо показник, що виступає статистичною вагою (f), відсутній і його слід додатково визначити на основі відомих варіант (x) і добутку варіант на частоту (xf), використовують середню гармонійну зважену:

17

, (4.5)

де .

Контрольні запитання

1. Що є абсолютними величинами та їх значення?

2. Види одиниць виміру абсолютних величин.

3. Що є відносними величинами та їх значення?

4. Види одиниць виміру відносних величин.

5. Види відносних величин та їх характеристика.

6. Графічне зображення відносних та абсолютних величин.

7. Дайте визначення середньої величини.

8. Властивості середньої величини.

9. Види середніх величин.

10. У яких випадках використовується середня арифметична?

11. У яких випадках використовується середня гармонійна?

12. Властивості середньої арифметичної.

13. Спрощений спосіб розрахунку ― спосіб “моментів”.