
- •3 Модуль 1.
- •Тема 1. Методологічні засади статистики
- •1.1. Джерела статистики. Предмет та категорії статистики
- •1.2. Теоретичні та методологічні основи статистики
- •Тема 2. Статистичне спостереження
- •2.1. Зміст, форми, види та способи статистичного спостереження
- •2.2. План статистичного спостереження
- •Тема 3. Зведення та групування статистичних даних
- •3.1. Суть статистичного зведення та групування
- •3.2. Статистичні групування. Види групувань
- •3.3. Ряди розподілу в статистиці
- •Тема 4. Узагальнюючи статистичні показники
- •4.1. Абсолютні величини та їх значення в статистичних дослідженнях
- •4.2. Відносні величини в статистиці. Форми їх вираження
- •4.3. Види відносних величин
- •4.3 Суть і використання середніх величин
- •4.4 Види середніх величин та методи їх розрахунку
- •Тема 5. Аналіз рядів розподілу
- •5.1. Структурні середні в статистиці
- •5.2 Характеристика показників варіації
- •5.3 Спрощені способи розрахунку дисперсії
- •5.4 Дисперсія альтернативної ознаки
- •5.5 Загальна, групова, середня з групових і міжгрупова дисперсії. Правило додавання дисперсії
- •Тема 6. Аналіз концентрації диференціації та подібності розподілів
- •6.1 Показники асиметричності розподілу
- •6.2 Аналіз локалізації, інтенсивності структурних зрушень та подібності структур
- •Тема 7. Статистичні методи вимірювання взаємозв'язків
- •7.1 Види взаємозв’язків між явищами
- •7.2 Основи кореляційно-регресійного аналізу
- •Тема 8. Аналіз інтенсивності динаміки
- •8.1. Динамічні ряди, їх види та правила побудови
- •8.2. Показники динамічного ряду
- •Тема 9. Аналіз тенденцій розвитку та коливань
- •9.1 Методи виявлення тенденцій розвитку в динамічних рядах
- •9.2 Інтерполяція і екстраполяція. Прогнозування суспільних явищ. Аналіз сезонних коливань
- •Тема 10. Індексний метод
- •10.1. Суть індексів та їх роль у статистичному аналізі
- •10.2. Агрегатний індекс ― основна форма загальних індексів
- •10.3. Середньозважені індекси
- •10.4. Індекси зі змінною і постійною вагою
- •10.5. Індекси змінного та фіксованого складу. Індекси структурних зрушень
- •Тема 11. Вибірковий метод
- •11.1. Загальне поняття про вибіркове спостереження
- •11.2. Види та способи відбору одиниць із генеральної сукупності
- •11.3. Помилки вибіркового спостереження
- •11.4. Визначення обсягу вибірки
- •Тема 12. Подання статистичних даних: таблиці, графіки, карти
- •12.1 Роль і значення графічного методу
- •12.2 Основні елементи графіка. Правила побудови статистичних графіків.
- •12.3. Види статистичних графіків і способів їх побудови
5.3 Спрощені способи розрахунку дисперсії
Спосіб 1. Варіанти виражені невеликими та небагатозначними числами:
![]() (5.11)
(5.11)
![]() ;
;
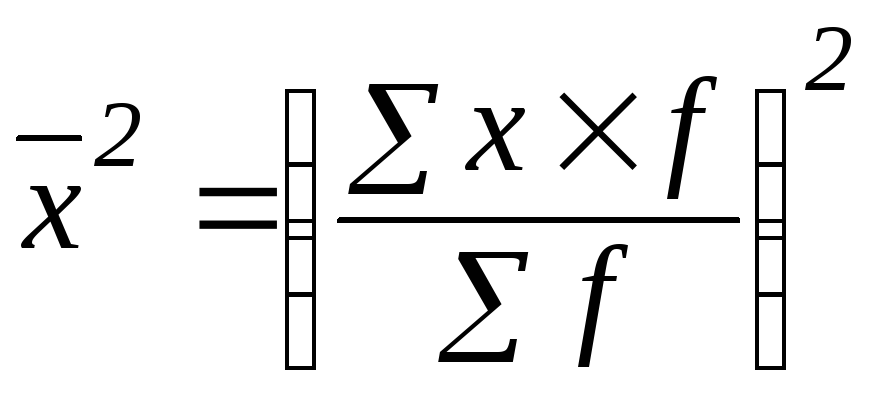 (5.12)
(5.12)
Спосіб 2. Використовується для рядів розподілу з рівними інтервалами.
Визначаючи цим способом дисперсію, треба знати деякі її властивості:
зменшення всіх значень ознаки на одну й ту ж величину А, величини дисперсії не змінює;
зменшення всіх значень ознаки в d разів, зменшує дисперсію в d2 разів.
![]() ,
(5.13)
,
(5.13)
де т1 ― момент першого порядку:
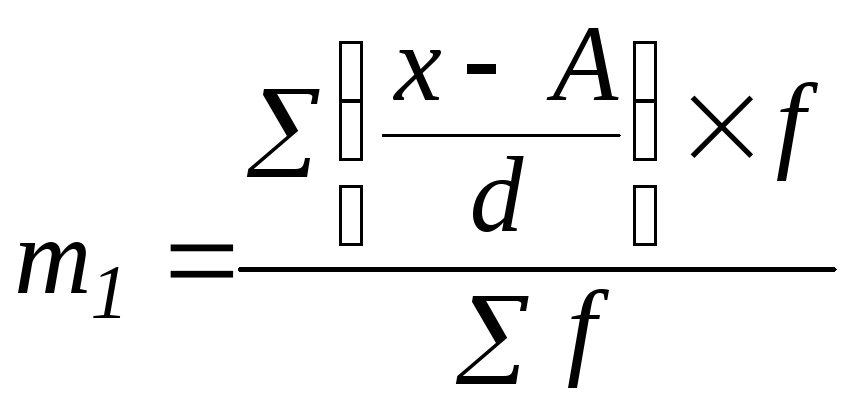 ,
(5.14)
,
(5.14)
т2 ― момент другого порядку:
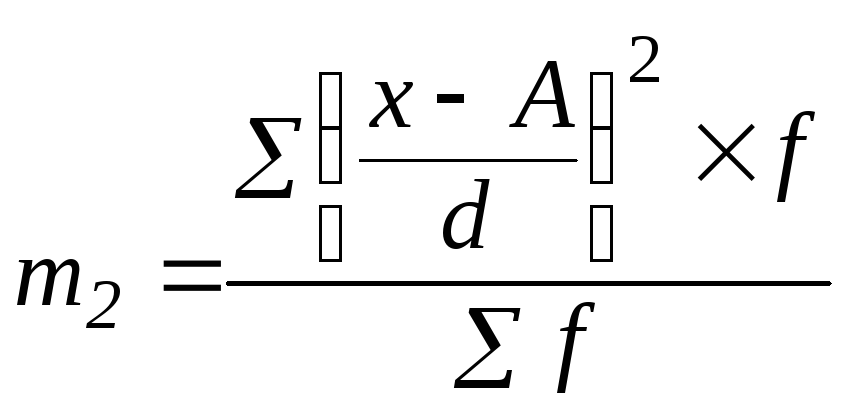 (5.15)
(5.15)
5.4 Дисперсія альтернативної ознаки
Бувають випадки, коли вивчають не середню величину ознаки, а частку одиниць, які мають або не мають тієї ознаки ― дисперсію альтернативної ознаки.
Відсутність альтернативної ознаки в тієї чи іншої одиниці сукупності приймаємо за “0”, а наявність цієї ознаки ― “1”. Тоді частину одиниць, які мають цю ознаку, визначаємо як “р”, а частину одиниць, які не мають ознаки ― “q”. Якщо p + q = 1, то q = 1 – p.
Тоді середнє значення альтернативної ознаки:
![]() (5.16)
(5.16)
Тобто, середнє значення альтернативної ознаки дорівнює частці тих одиниць, які мають цю ознаку.
Дисперсія альтернативної ознаки:
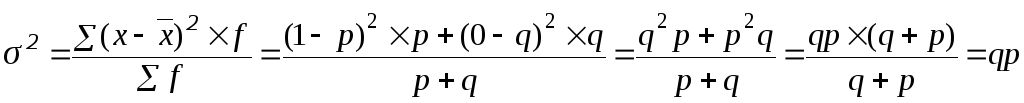 (5.17)
(5.17)
21
Дисперсія альтернативної ознаки являє собою добуток часток, які мають і не мають певної ознаки.
5.5 Загальна, групова, середня з групових і міжгрупова дисперсії. Правило додавання дисперсії
Вивчаючи варіацію тієї чи іншої ознаки, необхідно визначити вплив окремих факторів, які характеризують цю варіацію цілком. Виявити частку варіації, визначену тим чи іншим фактором, можливо за допомогою роз’єднання всієї сукупності на групи з ознаки, вплив якої досліджується.
Варіацію згрупованих даних завжди оцінюють дисперсією.
Види дисперсій:
загальна
![]() ;
;
групова
![]() ;
;
середня з
групових
![]() ;
;
міжгрупова
![]() .
.
Загальна варіація ознаки в сукупності повинна визначатися як сума варіації за рахунок одного виділеного фактора і за рахунок решти факторів:
![]() (5.18)
(5.18)
Загальна дисперсія дорівнює сумі середній з групових і міжгрупової дисперсії, тобто має місце правило додавання дисперсій.
Це правило широко використовується при необхідності спрощеного визначення будь-якого виду дисперсії.
Контрольні запитання
Що таке мода та її розрахунок в дискретних та інтервальних рядах розподілу?
Що таке медіана та її розрахунок в дискретних та інтервальних рядах розподілу?
Що уявляє собою варіація і від чого залежить її розмір?
Що таке розмах варіації та недоліки цього показника?
Що таке середнє лінійне відхилення та дисперсія?
Методи розрахунку дисперсії.
Дисперсія альтернативної ознаки.
Коефіцієнт варіації та умови його застосування.
Види дисперсій та їх характеристика. Правило додавання дисперсій.
22
Тема 6. Аналіз концентрації диференціації та подібності розподілів
6.1 Показники асиметричності розподілу
У
симетричних рядах розподілу значення
моди та медіани збігаються з середньою
величиною
![]() ,
а в помірно асиметричних вони
співвідносяться таким чином:
,
а в помірно асиметричних вони
співвідносяться таким чином:
![]() .
.
В аналізі закономірностей розподілу використовуються також інші порядкові характеристики: квартилі та децилі.
Квартилі Q – це значення варіант, які ділять упорядкований ряд за обсягом на чотири рівних частини, а децілі D – не десять рівних частин. Отже, в ряду розподілу визначаються три квартиі та дев’ять децилів. Медіана є водночас другим квартилем та п’ятим децилем. Розрахунок квартилів та децилів ґрунтується на кумулятивних частотах (частках).
Якщо
центр розподілу представлений медіаною,
то використовують квартильний
коефіцієнт варіації:
![]() .
Мірою оцінки розташування сукупності
слугує такожкоефіцієнт
децильної диференціації
.
Мірою оцінки розташування сукупності
слугує такожкоефіцієнт
децильної диференціації
![]() .
.
Найпростішою
мірою асиметричності розподілу є
відхилення між характеристиками центра
розподілу. Оскільки у симетричному
розподілі
![]() ,
то чим помітніша асиметрія, тим більше
відхилення (
,
то чим помітніша асиметрія, тим більше
відхилення (![]() ).
Стандартне відхилення називаютькоефіцієнтом
асиметрії
).
Стандартне відхилення називаютькоефіцієнтом
асиметрії
![]() .
У разі правосторонньої асиметрії
.
У разі правосторонньої асиметрії![]() ,
лівосторонньої -
,
лівосторонньої -![]() .
.
