ТОИИТ / Задания
.pdf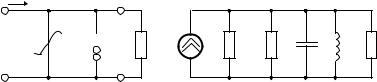
|
|
|
|
251 |
G |
=1/ R |
= r / ρ2 |
, |
(13.11) |
вн |
вн |
вн |
|
|
в случае синхронной накачки равная |
|
|
||
Gвн = −kmω0C0 cos(2ϕ) . |
(13.12) |
|||
i(t)
Gнэ |
Im GI |
Gвн С(t) L Gнэ |
C(t)  L
L
а |
б |
Рис. 13.3
Напряжение на нагрузке и рассеиваемая в ней мощность равны:
Um' = Im / (Gг + Gн.э + Gвн );
P' |
= 0.5I 2 G |
/ (G +G |
+G |
)2 . |
(13.13) |
H |
m н.э |
г н.э |
вн |
|
|
При отсутствии параметрической модуляции (т. е. при Gвн = 0 ) имеем
Um = Im / (Gг +Gвн ),
Pн = 0.5Im2 Gн.э / (Gг +Gн.э )2 ,
следовательно, коэффициенты усиления напряжения и мощности
|
U ' |
G +G |
|
|
Ky = |
m |
= |
г н.э |
; |
|
|
|||
|
Um |
Gг + Gн.э + Gвн |
||
|
|
|
P' |
(G + G |
)2 |
|
|
|
|||
K |
p |
= |
n |
= |
г |
|
н.э |
|
|
. |
(13.14) |
|
(G + G |
+ G |
)2 |
||||||||
|
|
Pn |
|
|
|||||||
|
|
|
|
|
г |
н.э |
|
вн |
|
|
|
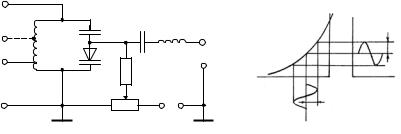
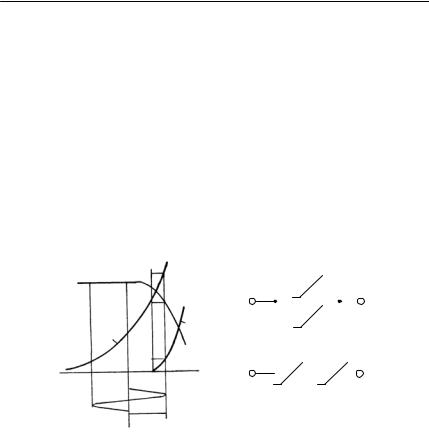
На рис. 13.4 показана схема одного из практических вариантов одноконтурного параметрического усилителя на варикапе, где
L,C (t) – собственно параметрический контур. Для согласования
253
Cср = (Cmax + Cmin )/ 2 > C0 , уменьшается характеристическое со-
противление и резонансная частота контура. В результате уменьшается вносимое сопротивление.
При диссипативном механизме ограничение амплитуды происходит за счет увеличения потерь в контуре, что обусловлено нели-
нейностью вольт-амперной характеристики i(u) p-n-перехода (рис. 13.5, а). С ростом амплитуды генерируемых колебаний увеличивается Iср = (imax −imin )/ 2 , уменьшается Rcp (U ) = (imax −imin ) / 2 и, следовательно, возрастает последовательное сопротивление rср (U )= ρ2 / Rср (U ) и суммарное сопротивление потерь(рис. 13.6, а)
|
rп = r + rср(U ) . |
(13.17) |
||||||||||||
R(u) |
|
Cmax |
|
|
|
Сср(U) |
||||||||
Rmax |
R0 |
|
|
|
||||||||||
Rmin |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C(u) |
C0 |
i(u) |
|
|
|
|
Rср(U) |
|||||||
|
|
|
|
|||||||||||
|
|
|
|
б |
||||||||||
|
|
imax |
||||||||||||
Cmin |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
0 |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
rср(U) |
|
|
Cср(U) |
|||||||||
|
U |
t |
в |
|
|
|
a |
Рис. 13.5
С учетом изложенного эквивалентная схема генератора, представленная на рис. 13.6, а, содержит активные сопротивления r ,
rср (U ), rвн . От сопротивлений можно перейти к проводимостям
G = r / ρ2 , Gср (U )= rср (U )/ ρ2 , Gвн = rвн / ρ2 (рис. 13.6, б).
Практические схемы параметрических генераторов (параметронов) отличаются от изображенных на рис. 13.6 и построены по балансному принципу (рис. 13.7), что обеспечивает подавление на выходе генератора колебания с частотой накачки.


255
Для рассматриваемой автономной системы в соответствии с законом сохранения энергии для средних мощностей в цепях имеем
Pc + Pн + Pк = 0 .
Это равенство должно выполняться тождественно для любых fc и fк , что имеет место лишь при
P / f |
c |
+ mP / (mf |
c |
+ nf |
н |
)= 0, |
|
|
c |
к |
|
|
|
(13.19) |
|||
P / f |
|
+ nP / (mf |
|
|
+ nf |
|
)= 0. |
|
|
н |
к |
c |
н |
|
|
||
н |
|
|
||||||
Уравнения (13.19), называемые уравнениями Мэнли-Роу, определяют перераспределение мощностей в многоканальной системе.
Отметим важную особенность такой системы – нечувствительность системы к соотношению фаз сигнала и накачки.
В схеме рис. 13.8 сигнал и комбинационное колебание функционируют в двух контурах, поэтому такую систему называют двухконтурной. Система может содержать несколько контуров, настроенных на различные комбинационные частоты.
13.3.ЗАДАЧИ
13.3.1.ВНОСИМОЕ СОПРОТИВЛЕНИЕ
1.К зажимам параметрического конденсатора приложено
небольшое |
гармоническое колебание |
uc (t) =Uc sin(ω0t + ϕ) |
(рис. 13.9, |
а-в). Емкость конденсатора |
изменяется по закону |
C(t) = C0 + |
C sin(ωнt) (рис. 13.9, г) в режиме синхронной накачки, |
|
т. е. ωн = 2ω0 .
Определите характер (знак) вносимого сопротивления, если напряжение на емкости имеет вид: а) рис. 13.9, а; б) рис. 13.9, б;
в) рис. 13.9, в.
2. Напряжение сигнала на параметрической емкости C (t )
изменяется |
по гармоническому закону |
uc (t) =Uc cos(ω0t + ϕ0 ) . |
||||||
Емкость |
|
конденсатора |
] |
изменяется |
во времени C (t )= |
|||
= C |
1+ m cos(2ω t + ϕ |
н |
) |
. |
|
|||
0 |
[ |
c |
0 |
|
|
|
||
Определите наименьшее по модулю значение ϕн , при котором: а) rвн = rвн.max , если ϕ0 = 45° ; б) rвн = 0 , если ϕ0 = 30°.

257
Qэ/Q
A
1.0 B C
0 rвн
Рис. 13.11
7. Параметрический контур образован емкостью C = 500 пФ и индуктивностью L(t) = 500 + L cos(ωнt) мкГн. Сопротивление по-
терь контура 20 Ом.
Определите, с какой частотой и в каких пределах надо изменять индуктивность контура, чтобы его эквивалентная добротность стала равной 400. Вычислите также коэффициент усиления напряже-
ния Kу .
8. Вычислите эквивалентную добротность и коэффициент усиления последовательного колебательного контура (рис. 13.1), образованного индуктивностью 1 мГн, емкостью
C(t) =1000 + 70cos(2π 106 t) пФ;
сопротивление потерь контура 40 Ом. Определите также полосу пропускания контура при наличии и отсутствии модуляции емкости.
9. Параметрический усилитель, схема которого приведена на рис. 13.1, предназначен для усиления сигналов в синхронном ре-
жиме на частоте ω0 = ωp = 2π 106 рад/с. Индуктивность и сопро-
тивление потерь контура соответственно равны: 160 мкГн и 25 Ом. Определите смещение и амплитуду напряжения накачки на варикапе, вольт-фарадная характеристика которого приведена на рис. 13.10 (и может аппроксимироваться линейной зависимостью в
окрестности U0 ), для получения коэффициента усиления напряже-
ния Ky =10 .
10. По данным предыдущей задачи определите максимально допустимое значение амплитуды вариации емкости и напряжения накачки, при которых усилитель сохраняет устойчивость.

258ГЛАВА 13. ПРИНЦИП УСИЛЕНИЯ И ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ
11.На вход параметрического усилителя (рис. 13.2) подается сигнал uвх(t) = 0.01cos(2π 106 t) В. Параметры усилителя: C = 500 пФ,
L(t) = 500 +10cos(4 106 t) мкГн, r = 25 Ом.
Вычислите коэффициент усиления напряжения. Постройте временную диаграмму огибающей выходного напряжения.
12. Параметрический усилитель, представленный эквивалентной схемой рис. 13.3, б, имеет параметры: Gг = 2 10−3 Cм, Gн.э = 2.5 10−3 См, ω0 = ωp . При какой величине вносимой прово-
димости Gвн коэффициент усиления мощности составит: а) 20 дБ
б) 40 дБ; в) бесконечно большую величину, т. е. усилитель окажется на пороге самовозбуждения.
13. Параллельный параметрический контур (рис. 13.3) функционирует в режиме синхронной синфазной накачки на резонанс-
ной частоте ω0 = ωp =107 рад/с. Найдите напряжение на нагрузке и рассеиваемую в ней мощность при наличии и отсутствии модуляции
емкости, если известны: |
Rг = 40 кОм, Rн.э = 20 кОм, Im = 0.25 мА, |
C(t) =1000 +10cos(2ωpt) |
пФ. Определите также коэффициент уси- |
ления мощности. |
|
14.По данным предыдущей задачи определите добротность Qэ
иполосу пропускания 2Δω0.7э при наличии и отсутствии модуля-
ции емкости.
15. Параллельный параметрический контур имеет параметры: Gг = Gн.э =10−4 См, ωp = ω0 =107 рад/с. Вольт-фарадная характе-
ристика варикапа, приведенная на рис. 13.10, аппроксимируется в окрестности рабочей точки U0 = 2 В выражением C(u) = 235 +
+75(u + 2) пФ. Емкость изменяется по гармоническому закону в режиме синхронной синфазной накачки.
Определите амплитуду напряжения накачки Uн , при которой: а) коэффициент усиления мощности Kp =18 ; б) усилитель теряет
устойчивость.
16. Схема параметрического усилителя показана на рис. 13.4, там же приведена зависимость C (u). Полагая, что усиление про-
исходит в синхронном синфазном режиме накачки, проиллюстрируйте характер зависимости коэффициента передачи К : а) от ам-

259
плитуды напряжения накачки Uн при постоянном смещении U0 ; б) от смещения U0 при постоянной амплитуде накачки Uн .
17. Входной сигнал частоты ω0 = ωp поступает в контур пара-
метрического усилителя (рис. 13.4) через выводы 1-2 катушки L , т. е. через L1 . Выходной сигнал снимается со всей катушки L . Параметры
контура: r =10 Ом, L =1 мкГн, C(t) =1000 +10cos(2π 106 t) пФ.
Определите L1 и p = L1 / L , обеспечивающие согласование кон-
тура с источником сигнала, внутреннее сопротивление которого равно 50 Ом. Вычислите также коэффициенты передачи К , усиле-
ния напряжения Ky и мощности Kp .
13.3.3.ПАРАМЕТРИЧЕСКАЯ ГЕНЕРАЦИЯ
18.Схема параметрического генератора с использованием варикапов изображена на рис. 13.7, а; при этом в каждом «плече» схемы включены параллельно два варикапа, вольт-фарадная характеристика которых приведена на рис. 13.10. Рассчитайте резонансную частоту контура и минимальное значение амплитуды модуля-
ции емкости Cmin и напряжения накачки Uн.min , необходимое для возбуждения контура, если U0 = −4 В, L =160 мкГн, Q = 40 .
19. Схема параметрического генератора дана на рис. 13.7, б. Параметры схемы:
C = 500 пФ, r = 25 Ом и L(t) = 500 + L cos(4 106 t) мкГн.
Определите наименьшее значение амплитуды модуляции индуктивности ( Lmin ), при котором генератор самовозбудится.
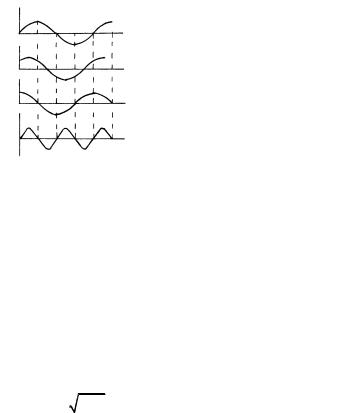
20.На рис. 13.12 показаны амплитудно-частотные характеристики (АЧХ) параметрического генератора.
Какие из механизмов ограничения амплитуды генерируемых колебаний, иллюстрированных на рис. 13.13, соответствуют заданной АЧХ: а) рис. 13.12, а; б) рис. 13.12, б; в) рис. 13.12, в?
21.Пороговые характеристики генератора на варикапе (КВ105)
показаны на рис. 13.14. Характеристика C(u) аппроксимирована выражением:
C(u) = C(0) ϕk /(ϕk + u) , где C(0) =1470 пФ, ϕk = −0.6 В.