Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт информационных технологий БГУИР

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТОИИТ / Задания

.pdf

Скачиваний:

126

Добавлен:

24.02.2016

Размер:

9.82 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2829 / 3629 30 31 32 33 34 35 36 > Следующая >>>

281

В качестве исходного при синтезе двухполюсников обычно используют входное сопротивление

Z (p)=			a pn + a		pn−1		+... + a p + a
			n	n−1			1		0		=
		b		pm + b		pm−1 +... + b p + b

			m	m−1			1		0
=	a0 (p − z1 )(p − z2 )...(p − zn )
										.
	b		(p − p )(p		− p		)...(p − p	m	)
0				1		2

Если задана функция Z ( p) , то она может быть реализована пас-

сивной цепью при выполнении следующих условий: 1) все коэффициенты многочленов числителя и знаменателя вещественны и положительны; 2) все нули и полюсы находятся либо в левой полуплоскости, либо на мнимой оси, причем полюсы и нули на мнимой оси простые; данные точки всегда либо вещественны, либо образуют комплексно-сопряженные пары; 3) высшие и низшие степени многочленов числителя и знаменателя отличаются не более чем на единицу. Следует отметить также, что процедура синтеза не является однозначной, т. е. одну и ту же входную функцию можно реализовать несколькими способами.

В качестве исходных структур синтезируемых двухполюсников обычно используют цепи Фостера, представляющие собой последовательное либо параллельное соединение относительно входных зажимов соответственно нескольких комплексных сопротивлений и проводимостей, а также лестничных цепей Кауэра [2].

Метод синтеза двухполюсников основан на том, что заданная входная функция Z (p) или Y (p) подвергается ряду последова-

тельных упрощений. При этом на каждом этапе выделяется выражение, которому ставят в соответствие физический элемент синтезируемой цепи. Если все компоненты выбранной структуры идентифицированы с физическими элементами, то задача синтеза решена.

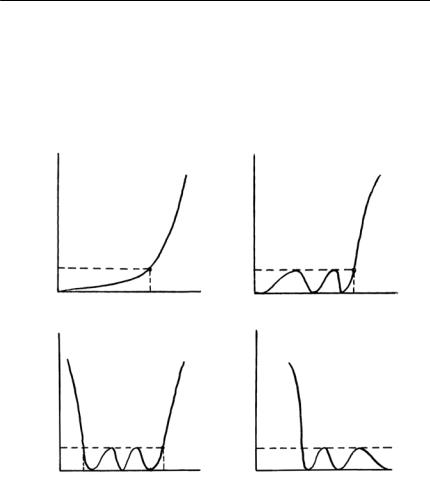
Синтез четырехполюсников базируется на теории фильтровпрототипов нижних частот [2]. Возможные варианты прототипа ФНЧ показаны на рис. 15.1.

При расчете может быть использована любая из схем, так как их характеристики идентичны. Обозначения на рис. 15.1 имеют сле-

дующий смысл: qk =1,n – индуктивность Lk′ последовательной ка-

тушки или емкость Сk′ параллельного конденсатора; q0 – сопротивление генератора R0′ , если q1 = Ck′ , или проводимость генерато-

ра G0′ ,	если q1 = L1′; qn+1 – сопротивление нагрузки Rn′+1 , если
qn = Cn′	или проводимость нагрузки Gn′+1 , если qn = Ln′ .

282 ГЛАВА 15. ЭЛЕМЕНТЫ СИНТЕЗА ЛИНЕЙНЫХ СТАЦИОНАРНЫХ ЦЕПЕЙ

L′2=g2		L′n=gn
R′0=g0	C′3=g3	G′n+1=gn+1	R′n+1=gn+1
C′1=g1	C′3=g3	C′n=gn
		а
L′1=g1 L′3=g3		L′n=gn
G′0=g0		R′n+1=gn+1	G′n+1=gn+1
C′2=g2	C′n=gn

Рис. 15.1

Величины элементов прототипов нормируют так, чтобы q0 =1 и частота среза ω1′ =1 . Переход от нормированных фильтров-

прототипов к другому уровню сопротивлений и частот осуществляется с помощью следующих преобразований элементов цепи:

R =

или G =

G' ;

ω'

L =

;

ω'

C =

C' =

C' .

Величины со штрихами относятся к нормированному прототипу, а без штриха – к преобразованной цепи. Исходной величиной при синтезе является рабочее затухание мощности, выраженное в децибелах:

LA (ω' )=10 lg х[Pm / Pвых(ω)] , дБ,

Pm = Eвх2 / 4R0 – максимальная мощность генератора с внутренним сопротивлением R0 и ЭДС Eвх , Pвых (ω) – выходная мощность в нагрузке.

283

Обычно частотную зависимость LA (ω' ) аппроксимируют максимально плоской (баттервортовской) характеристикой (рис. 15.2, а)

LA (ω' )=10 lg[1 + ε(ω′/ ω1′)2n ] , дБ,

где ε =10(LAr /10) −1.

Lа, дБ

Lar			Lar
0	ω′1	ω′	0	ω′1	ω′
	а		0	б
	а			б
Lа, дБ			Lа, дБ
Lа, дБ

Lar			Lar
0 ω1	ω0	ω2 ω	0	ω1	ω
	в			г

Рис. 15.2

Величину рабочего затухания LAr , соответствующую частоте

среза ω1' , обычно выбирают равной 3 дБ. При этом ε =1 . Параметр

n равен числу активных элементов цепи и определяет порядок фильтра.

Величины элементов максимально плоских фильтров, нагруженных на активное сопротивление на входе и выходе и имеющих

LAr = 3 дБ, q0 =1 и ω1' =1 , определяют из выражений

284 ГЛАВА 15. ЭЛЕМЕНТЫ СИНТЕЗА ЛИНЕЙНЫХ СТАЦИОНАРНЫХ ЦЕПЕЙ

q0 = qn+1 =1 ;

	(2k −1)π	, k =1, 2,..., n .
qk = 2sin	2n

Широкое распространение получила также равнопульсирующая аппроксимация Чебышева (см. рис. 15.2, б)

	A (	'	)			2	'
L		'			+ εT	2	ω	,
		ω		=10lg 1
		ω		=10lg 1			'
					n		'
							ω
							1

где Tn (x)= cos (narccos (x)) – полином Чебышева n-го порядка для x ≤1 , T0 (x)=1, T1 (x)= x , T2 (x)= 2x2 −1, T3 (x)= 4x3 −3x и т. д.,

Tn (x)= ch (narch (x)) для x >1 ; x = ω′/ ω1′.

Полиномы n-го порядка могут быть найдены с помощью рекуррентного соотношения. Основное преимущество чебышевских фильтров по сравнению с максимально плоскими (Баттерворта) – меньшее число элементов, требующееся для обеспечения одинакового затухания на заданной частоте вне полосы пропускания.

Для чебышевских фильтров, нагруженных с двух сторон и

имеющих характеристики вида рис. 15.2, б при условии, что ω' =1 и q0 =1 , а LAr задано в децибелах, величины элементов могут

быть рассчитаны следующим образом. Сначала определяются вспомогательные параметры по формулам:


				L	Ar			γ = sh(β/ 2n);
β = ln cth					Ar		;
β = ln cth			17.37				;
			17.37
		(2k −1)π						,	k =1, 2,..., n ,
αk = sin				2n				,	k =1, 2,..., n ,
				2n
b	= γ2 + sin2					kπ		,	k =1, 2,..., n ,
b	= γ2 + sin2							,	k =1, 2,..., n ,
k
							n

затем находят величины элементов

q1 = 2 γa1 ;

285


q	=	4ak −1ak		,	k =1, 2,..., n ;

k		bk −1qk −1

	1,		если n нечетное,
qn+1 =
	cth2		(β/ 4),		если n четное.

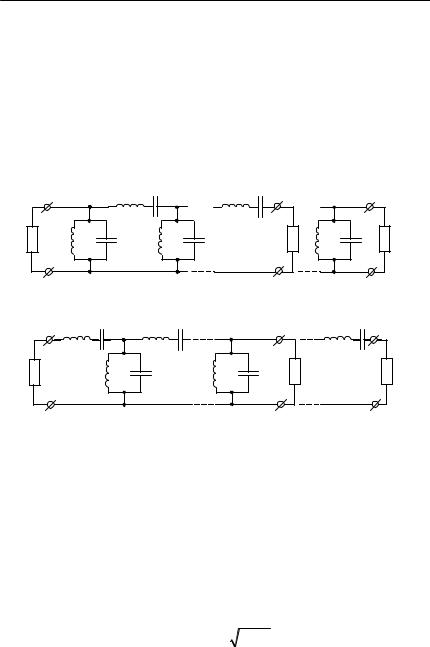
С помощью прототипа ФНЧ можно рассчитать полоснопропускающие фильтры (ППФ), структуры которых показаны на рис. 15.3.

	L2	C2	Ln	Cn n – четн. n – нечетн.
R0	L1	L3		Gn+1 Ln	Rn+1
	C1	C3		Cn

				а
				n –четн.	n – нечетн.
L1	C1	L3	C3		Ln	Cn
R0	L2	C2	Ln	Cn	Rn+1	Gn+1
		C2		Cn

Рис. 15.3

Переход от структур прототипов ФНЧ рис. 15.1, а, б к соответствующим ППФ рис. 15.3, а, б выполняют с помощью частотного преобразования

ω' =	ω'	ω		ω
	1		−	0	.
	1	ω0	−	0	.
	W	ω0		ω

Полосу пропускания и ее среднюю частоту определяют из выражений


W =	ω2	− ω1	; ω = ω ω .
W =			; ω = ω ω .
		0		1	2
	ω0

286 ГЛАВА 15. ЭЛЕМЕНТЫ СИНТЕЗА ЛИНЕЙНЫХ СТАЦИОНАРНЫХ ЦЕПЕЙ

Параметры последовательных и параллельных резонаторов рассчитывают по формулам

	ω C =			1		=		ω1' qi	– для параллельных резонаторов;
	ω C =		ω L			=	WR		– для параллельных резонаторов;
	0	i	ω L				WR
				0	i		0
ω L =		1			=	ω1' qk R0			– для последовательных резонаторов.
ω L =		ω C			=	ω1' qk R0			– для последовательных резонаторов.
0	k	ω C		k			W
		0		k

В этих выражениях qi – значения параметров элементов прототипа, а частоты ω1 , ω0 , ω2 показаны на характеристике ППФ (см.

рис. 15.2, в).

Переход от прототипа ФНЧ к структуре фильтра верхних частот (ФВЧ) (рис. 15.4) происходит с помощью частотного преобразования

		'	ω1' ω1
		ω = −	ω	,
здесь ω1 – частота среза (см. рис. 15.2, г).
	C1	C3	n – четн.		n – нечетное
	C1	C3			Cn
R0	L2	L4		Ln	Rn+1	Rn+1
	L2	L4		Ln

Рис. 15.4

При этом расчет параметров элементов ФВЧ производится по формулам:

Ci =		1			;
Ci =	ω' ω q R				;
	1	1	i	0
L =		1		R	;
L =	ω' ω q			R	;
k	ω' ω q		k	0
	1	1	k

Rn+1 = R0 qn+1 .q0

p2 + 4

287

15.3.ЗАДАЧИ

15.3.1. СИНТЕЗ ДВУХПОЛЮСНИКОВ

1. Осуществите реализацию двухполюсника по Фостеру в виде последовательного соединения элементов по заданной функции входного сопротивления

Z (p)= p4 +10 p2 + 9 . p3 + 4 p

2. Реализуйте функцию Z (p) предыдущей задачи по второй форме Фостера в виде параллельного соединения проводимостей.

3.Получите различные варианты реализации по Кауэру двухполюсника, обладающего входным сопротивлением задачи 1.

4.Реализуйте в виде лестничной цепи Кауэра двухполюсник с входным сопротивлением

Z (p)= p(p2 +9).

5. Определите, может ли данное выражение быть функцией входного сопротивления некоторой электрической цепи:

а)	2 p2			−5 p +1			;
		p	2	+ p +1

в)		p2				;
	5 p2			+	6

д)		p4	+ 26 p2 + 25						;
				p3	+ 4 p

ж)		p4		+10 p2 + 9				.
			p3		+ 4 p

б)		9 p			;
	(2 p +1)(p2 + p +1)
г)	(p +1)(p + 3)			;
	p (p + 2)
е)	p2 + p +1		;
	1 + p2

15.3.2.СИНТЕЗ ЧЕТЫРЕХПОЛЮСНИКОВ

6.Рассчитайте параметры элементов ФНЧ с максимально плоской характеристикой затухания, с числом элементов цепи n = 5 и

288 ГЛАВА 15. ЭЛЕМЕНТЫ СИНТЕЗА ЛИНЕЙНЫХ СТАЦИОНАРНЫХ ЦЕПЕЙ

частотой среза ω1 = 2πf1 = 2π 105 рад/с и внутренним сопротивлением генератора R0 = 50 Ом.

7.Определите величину затухания ФНЧ (задача 6) на частоте f1 =1.2 105 Гц.

8.Определите порядок ФНЧ с плоской характеристикой и час-

тотой среза ω1 = 2π 105 рад/с, имеющего затухание не менее 30 дБ на частоте ω = 2π 1.25 105 рад/с.

9.Докажите, что при одинаковых исходных данных фильтры с чебышевской характеристикой имеют большее затухание за полосой пропускания по сравнению с фильтрами, имеющими плоскую характеристику затухания.

10.Сколько элементовов должен иметь ФВЧ с чебышевской харак-

теристикойзатухания L		Ar	=1.0 дБичастотойсреза ω = 2π 104 рад/с,
		Ar		LAr ≥ 20	1
чтобы	обеспечить	затухание		LAr ≥ 20	дБ	на	частоте
ω = 2π 0.8 104 рад/с?
1	Сколько резонаторов должен содержать ППФ с максимально
11.	Сколько резонаторов должен содержать ППФ с максимально
плоской характеристикой затухания, ω =104					рад/с,	ω	=1.6 рад/с,
				1		2

чтобы обеспечить затухание на частоте ω= 0.8 104 рад/с не менее

20дБ?

12.Чему равна мощность в нагрузке фильтра, если амплитуда

ЭДС генератора на входе Eвх = 20 В, внутреннее сопротивление генератора R0 = 50 Ом, а затухание фильтра LA =1;2;3;10;20 дБ?

15.4. КОНТРОЛЬНОЕ ЗАДАНИЕ. СИНТЕЗ ЧЕТЫРЕХПОЛЮСНИКА

По исходным данным, приведенным в табл. 15.1 и 15.2, произвести синтез четырехполюсника (фильтра) на основе фильтрапрототипа НЧ. Осуществить расчет параметров фильтра.

Таблица 1 5 . 1

Номер	0	1	2	3	4	5	6	7	8	9
варианта	0	1	2	3	4	5	6	7	8	9
Тип	ФНЧ	ФНЧ	ФВЧ	ФВЧ	ФВЧ	ППФ	ППФ	ППФ	ППФ	ППФ
фильтра

						289
						Таблица 1 5 . 2

Номер			Исходные данные фильтра
подва-
рианта	n	LAr , дБ	f1 , кГц	f2 , кГц	R0 Ом	Аппроксимация
0	4	0,1	10	12,5	50	Чебышева
1	4	0,2	20	25	75	Чебышева
2	5	3.0	30	35	50	Баттерворта
3	5	0,5	40	45	75	Чебышева
4	6	3.0	50	60	75	Баттерворта
5	6	1,0	60	70	50	Чебышева
6	7	3.0	80	100	50	Баттерворта
7	7	1,0	100	120	75	Чебышева
8	8	3.0	150	200	50	Баттерворта
9	8	2.0	200	250	75	Чебышева

Я думаю, нет большей ненависти в мире, чем ненависть невежд к знанию.

Галилео Галилей

ГЛАВА 16

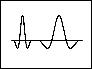
ОСНОВЫ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ СИГНАЛОВ

16.1.ИЗУЧАЕМЫЕ ВОПРОСЫ

Вейвлеты. Непрерывное и дискретное вейвлет-преобразование

(ВП). Характерные отличия от преобразования Фурье. Признаки, свойства и примеры материнских вейвлетов. Свойства вейвлетанализа и возможности ВП [31..34].

Указания. В конце настоящего раздела приведен обзор литературы по теории и практическому использованию ВП. Самые краткие общие сведения даны в учебнике [*.5], для более углубленного изучения возможностей ВП следует обратиться к одной из книг [*.1…*.4]. Подробные обзоры по ВП для тех, кто собирается применять это преобразование в практических расчетах и приложениях, приведены в работах [*.10, *.14]; при этом список литературы в [*.14] содержит 92 названия.

16.2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

В последние годы возникло и успешно развивается новое и важное направление в теории и технике сигналов, получившее название вейвлет-преобразования (ВП), которое хорошо приспособлено для изучения структуры неоднородных процессов. Это направление еще не так хорошо известно широкому кругу отечественных исследователей и инженеров, поскольку применяется сравнительно недавно и математический аппарат его находится в стадии активной разработки.

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2829 / 3629 30 31 32 33 34 35 36 > Следующая >>>

Соседние файлы в папке ТОИИТ

#
24.02.201622.54 Кб29Вопросы для экзамена по ТОИИТ.docx
#
24.02.20169.82 Mб126Задания.pdf
#
24.02.201690.11 Кб24Положение о контрольных работах зо.doc