Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт информационных технологий БГУИР

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТОИИТ / Задания

.pdf

Скачиваний:

126

Добавлен:

24.02.2016

Размер:

9.82 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 3132 / 3632 33 34 35 36 > Следующая >>>

ПРИЛОЖЕНИЯ

П.1. НЕКОТОРЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ

ФОРМУЛЫ ПРИВЕДЕНИЯ

cos(90o ± α) = msin α , sin(90o ±α) = +cos α , tg(90o ±α) = mctgα , cos(180o ± α) = −cos α , sin(180o ±α) = msin α , tg(180o ±α) = ±tgα , cos(270o ±α) = ±sin α , sin(270o ±α) = −cos α , tg(270o ±α) = mctgα , cos(360o −α) = +cos α , sin(360o −α) = −sin α , tg(360o −α) = −tgα .

ФОРМУЛЫ СУММЫ И РАЗНОСТИ УГЛОВ И ФУНКЦИЙ

cos(α ±β) = cos αcosβ msin αsin β, sin(α ±β) = sin αcosβ ± cos αsin β,

cos α + cosβ = 2cos[(α +β) / 2]cos[(α −β) / 2] , cos α − cosβ = −2sin[(α +β) / 2]sin[(α −β) / 2] , sin α + sin β = 2sin[(α +β) / 2]cos[(α −β) / 2] , sin α −sin β = 2cos[(α +β) / 2]sin[(α −β) / 2] .

ФОРМУЛЫ ПРОИЗВЕДЕНИЯ ФУНКЦИЙ

cos αcosβ = 0.5[cos(α −β) + cos(α +β) , sin αsin β = 0.5[cos(α −β) − cos(α +β) , sin αcosβ = 0.5[sin(α −β) + sin(α +β) .

ФОРМУЛЫ КРАТНЫХ АРГУМЕНТОВ

cos2 α = 0.5(1 + cos 2α) , cos3 α = (3/ 4) cos α + (1/ 4) cos3α , cos4 α = 3/ 8 + (1/ 2)cos 2α + (1/ 8)cos 4α ,

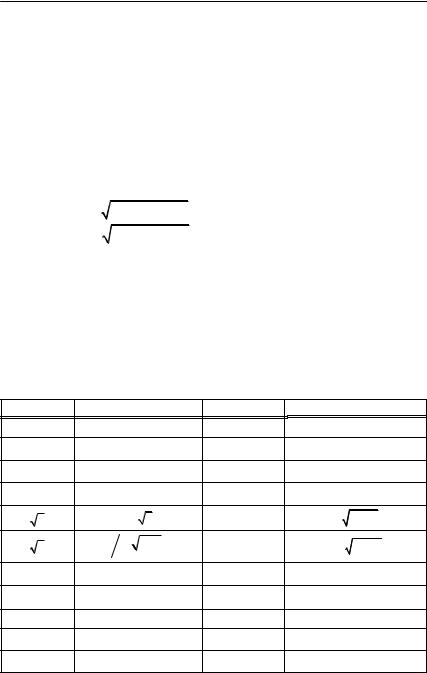
cos5 α = (5 / 8) cos α + (5 /16) cos3α + (1/16)cos5α ,

312						ПРИЛОЖЕНИЯ
sin2 α = 0.5(1 − cos 2α) , sin3 α = (3/ 4)sin− (1/ 4)sin 3α ,
sin4 α = 3/ 8 − (1/ 2) cos 2α + (1/ 8) cos 4α,
sin5 α = (5 / 8)sin α − (5 /16)sin 3α + (1/16)sin 5α .
ФОРМУЛЫ ДВОЙНЫХ, ТРОЙНЫХ И ПОЛОВИННЫХ УГЛОВ
sin 2α = 2sin αcos α ,
cos 2α = cos2 α −sin2 α =1− 2sin2 α = 2cos2 α −1,
cos 3α = 4cos3 α −3cos α ,
sin 3α = 3sin α − 4sin3 α ,
cos(α/ 2) = ±		0.5(1 + cos α) ,
sin(α/ 2) = ±		0.5(1 − cos α) .
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
shx = (ex − e−x ) / 2 ,			sin x = − jsh( jx) = (e jx − e− jx ) / 2 j ,
chx = (ex	+ e−x ) / 2		cos x = ch( jx) = (e jx + e− jx ) / 2 ,
e jωt = cos ωt + j sin ωt , e− jωt				= cos ωt − j sin ωt .
П.2. ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Функция		Производная		Функция	Производная
x		1		sin x		cos x
xn		nxn−1		cos x	– sin x
1/ x		– 1/ x2		tgx	1/ cos2 x = sc2 x
1/ xn		– n / xn+1		ctgx	– 1/ sin2 x = −csc2 x
x		1/(2	x )	arcsin x	1/	1 − x2
n x		1 (n n xn −1 )		arccos x	– 1/	1 − x2
eax		aeax		arctgx	1/(1 + x2 )
ax		ax ln x		arcctgx	– 1/(1 + x2 )
ln x		1/ x		shx		chx
loga x		l/(x ln a)		thx	1/ ch2 x
lg x	(lg e) / x ≈ 0.43/ x			cthx	– 1/ sh2 x

313

П.3. НЕКОТОРЫЕ ИНТЕГРАЛЫ

1.∫xndx = xn+1 /(n +1) ( n ≠ −1)

2.∫dx / x = ln x

3.∫eaxdx = (1/ a)eax

4.∫xeaxdx = (1/ a2 )eax (ax −1)

5.∫x2eaxdx = eax (x2 / a − 2x / a2 + 2 / a3 )

6.∫x peaxdx = (1/ a)x peax −( p / a)∫x p−1eaxdx

7.∫xe−ax2 dx = −(1/ 2a) e−ax2

8.∫x2e−x2 / 2dx = −x e−x2 / 2 + ∫e−x2 / 2dx

9.∫axdx = ax / ln a

10.∫sin αxdx = −(1/ α) cos αx

11.∫cos αxdx = (1/ α)sin αx

12.∫sin2 αxdx = x / 2 −(1/ 4α)sin 2αx

13.∫sin3 αxdx = −(1/ α) cos αx + (1/ 3α) cos3 αx

14.∫cos2 αxdx = x / 2 + (1/ 4α)sin 2αx

15.∫cos3 αxdx = (1/ α)sin αx −(1/ 3α)sin3 αx

16.∫xsin αxdx = (1/ α2 )sin αx −(x / α) cos αx

17.∫x cos αxdx = (1/ α2 ) cos αx + (x / α)sin αx

18.∫sin αx cos αxdx = (1/ 2α)sin2 αx

19.∫eax cosbxdx = (a2 +b2 )−1eax (a cosbx +bsin bx)

ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ X = a2 + x2

20.∫dx / X =Y / a , здесь и ниже Y = arctg(x / a)

21.∫dx / X 2 = x /(2a2 X ) +Y /(2a3 )

314	ПРИЛОЖЕНИЯ

22.∫dx / X 3 = x /(2a2 X 2 ) +3x /(8a4 X ) +3Y /(8a5 )

23.∫(x2 / X )dx =x − aY

24.∫(x2 / X 2 )dx = −(x / 2X ) +Y /(2a)

ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ

∞

sin x

1. ∫

dx = π/ 2

2. ∫

sin ax

dx = aπ/ 2

∞

sin2 x

∞

3. ∫

dx = π

4. ∫

при a > 0

a2 + x2

−∞

∞

3π

5. ∫

6. ∫

(a2 + x2 )2

4a3

(a2 + x2 )3

16a5

∞

x2dx

∞

x2dx

7. ∫

=∞

8. ∫

a2 + x2

(a2 + x2 )2

∞

9. ∫

( a > 0,b > 0 )

(a2 + x2 )(b2 + x2 )

2ab(a +b)

∞

x2k dx

(k −1)!(2n − k −3)!

10. ∫

(ax2 + c)n

2(2n − 2)!ak cn−k −1

∞

11. ∫e−αxdx =1/ α

( α > 0 )

∞

12. ∫xe−αxdx =1/ 2α

∞

13. ∫xne−αxdx = n!α−n−1

( α > 0 )

315

∞

14.

∫e−α2 x2 dx =

π / 2a

∞

15.

∫x2e−α2x2 dx =

π / 4a3

∞

16.

∫e−αx cos(mx)dx = α/(α2 + m2 )

∞

α2 − m2

17.

∫xe−αx cos(mx)dx =

(α

+ m

)

∞

18.

∫e−α2x2 cos(mx)dx =

e−b2 / 4α2

2α

∞

cos(mx)

19. ∫

dx =

e−ma

a2 + x2

∞

cos(mx)

(1 + ma)e−ma

20.

∫

+ x

)

∞

cos(mx)

πe

−ma

n−1

(2n − k − 2)!(2ma)

21.

∫

dx =

∑

(a2 + x2 )n

(2a)2n−1(n −1)!k =0

k!(n − k −1)!

( a > 0, m > 0 )

∞

cos(mx)

(1 − ma)e−ma

22.

∫

dx =

+ x

)

∞

cos(mx)

e−mb

e−ma

23.

∫

dx =

−

a ≠ b

+ x

)(b

+ x

)

2(a

−b

)

∞

x2 cos(mx)

(ae−ma −be−mb )

24.

∫

dx =

+ x

)(b

+ x

)

2(a

−b

)

∞

25.

∫ex2 / 2 =

2πφ (−z),

где φ(−z) =1 − φ(z) ,

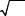
316			ПРИЛОЖЕНИЯ
		z
φ(z) =	1	∫ e−x2 / 2dx – табулированный интеграл вероятности
φ(z) =	2π	∫ e−x2 / 2dx – табулированный интеграл вероятности
		−∞
∞
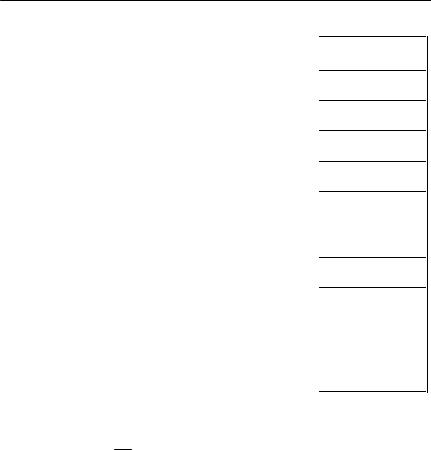
26. ∫x2 exp(−x2 / 2σ2x )dx =			π/ 2 σ3x
0

317

П.4. ОСНОВНЫЕ ТЕОРЕМЫ О СПЕКТРАХ

№	Название теоремы	S(t)
п/п	Название теоремы	S(t)
п/п
1	Теорема о спектре сигнала,	aS(t)
	умноженного на константу	aS(t)
	умноженного на константу
2	Теорема о спектре суммы	S1(t) +... + Sn (t)
	сигналов	S1(t) +... + Sn (t)
3	Теорема о спектре сигнала,	S(t m τ)
	смещенного во времени (τ)	S(t m τ)
	смещенного во времени (τ)
4	Теорема о смещении спектра	S(t)em jΩt
	сигнала
5	Теорема о спектре сигнала при	S(at)
	изменении масштаба времени	S(at)
	изменении масштаба времени

6	Теорема о спектре сигнала при	S(−t)
	инверсии оси времени	S(−t)
	инверсии оси времени
7	Теорема о спектре производ-	d (n)S /(dt)n
	ной от сигнала
8	Теорема о спектре сигнала,	t
	проинтегрированного по вре-	∫ S(t)dt
	мени	−∞
9	Теорема о спектре произведе-	S(t)U (t)
	ния сигналов	S(t)U (t)
	ния сигналов
10	Теорема о произведении спек-	S(t) U (t)
	тров сигналов	S(t) U (t)
	тров сигналов

S&(ω)

aS&(ω)

S&1(ω) +... + S&n (ω)

S&(ω)em jωτ

S&(ω± Ω)

1	&	ω
	S
a
	a

−S&(−ω)

( jω)n S&(ω)

(1/ jω)S&(ω)

S&(ω) U&(ω)

S&(ω)U&(ω)

– знак интеграла свертки:

S&(ω) U&(ω) = 1π ∞∫ S&(ξ)U&(ω−ξ)dξ;

2 −∞

∞

S(t) U (t) = ∫ S(τ)U (t − τ)dτ

−∞

П.5. ОБ АКТИВНОЙ ДЛИТЕЛЬНОСТИ И ШИРИНЕ СПЕКТРА ИМПУЛЬСНОГО СИГНАЛА

Вычисления выражений (2.13) и (2.14) для некоторых импульсных сигналов приведены в книге А. А. Харкевича “Спектры и

анализ” (М.: Физматгиз, 1962. – 236 с.). Выбирая kэ = 0.9 , получим результаты, приведенные в табл. П.1. Здесь μ = τэ fэ .

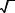
318

ПРИЛОЖЕНИЯ

Таблица П. 1

Импульс S(t)

S&(ω)

τэ

fэ

Прямоугольный

S0τ

sin(ωτ/ 2)

0.90τ

0.9

S(t) = S0 ,

≤ τ/ 2

ωτ/ 2

Экспоненциальный

1.155

0.98α

1.13

S(t) = S0e−αt , t > 0

α + jω

Треугольный

sin(ωτ/ 4) 2

0.84

2S0

0.54τ

0.46

S(t) =

−

≤ τ/ 2

ωτ/ 4

Косинусоидальный

2S0τ

cos(ωτ/ 2)

0.73

S (t) = S0 cos ω0t,

≤ τ/ 2 ,

0.596τ

0.43

1 − (ωτ/ π)2

τ = T / 2, T = 2π/ ω0

Колокольный

−ω2 / 4β2

0.825

0.26β

0.22

S(t) = S0e−β

Значение μ = τэ fэ

оказывается наибольшим у импульсов, ха-

рактеризующихся разрывом функции S(t) (экспоненциальный и прямоугольный импульсы), меньшим – у импульсов с разрывом первой производной S′(t) (треугольный и косинусоидальный) и

самым малым – у колокольного импульса, характеризующегося непрерывностью как функции S(t) , так и всех ее производных.

Из рассмотренного следует, что эффективная ширина спектра импульса связана с его длительностью зависимостью

fэ = μ/ τэ ,

где μ – коэффициент, зависящий от формы импульса и принятого уровня kэ полной энергии, а следовательно, и уровней τ и f .

Выбирая kэ = 0.95 (95 %), получаем результаты, приведенные в

табл. П.2, взятой из книги Я.С. Ицхоки “Импульсные устройства” (М.: Советское радио, 1959. – 728 с.

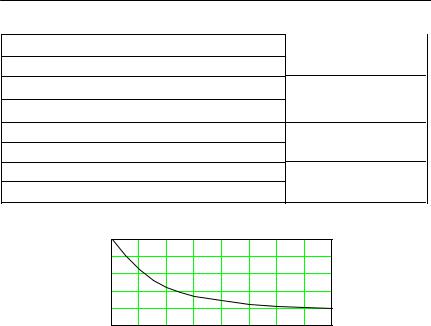
Оценку эффективной ширины спектра импульса можно произвести также с помощью графика рис. П.1. На нем и в табл. П.2 при-

няты обозначения: τ0.5 – длительность импульса, измеряемая на половинном уровне от амплитуды ( 0.5U ); tфа – активная длитель-

ность фронта, определяемая разностью соответствующих моментов времени достижения импульсом значений 0.9U и 0.1U .

								319
								Таблица П. 2
	Импульс							fэ = f0.95
Прямоугольный								2 / τ
С экспоненциальными фронтами τфа / τ0.5 = 0.2								0.9 / τ
С экспоненциальными фронтами τфа / τ0.5 = 0.1								1.37 / τ
Трапецеидальный								0.9 / τ
Треугольный								0.94 / τ
Косинусоидальный								1/ τ
Колокольный								0.31/ β
f0.95ф0.5
2
1.6
1.2
0.8
0.4
0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8 tфаф0.5
			Рис. П.1
П.6. СВЯЗЬ МЕЖДУ ИЗОБРАЖЕНИЕМ ПО ЛАПЛАСУ
И ОРИГИНАЛОМ

F ( p)	f (t)

1	δ(t)

1/ p	σ(t)

1/ p2 ; 1/ p3 ; 1/ p4	t ; t2 / 2 ; t3 / 6
1/( p + a)	e−at
p /( p + a)	δ(t) − ae−at
1/[ p( p + a)]	(1/ a)(1 − e−at )
1/[ p( p + a)2 ]	(1/ a2 )(1 − e−at − ate−at )
p /( p2 − a2 )	ch(at)
1/[( p + a)( p + b)]	[1/(b − a)](e−at − e−bt )

320					ПРИЛОЖЕНИЯ

p /[( p + a)( p + b)]			[1/(a −b)](ae−at −be−bt )
1/( p + a)2			te−at
p /( p + a)2			(1 − at)e−at
1/( p + a)3			(t2 / 2)e−at
p /( p + a)3			t(1 − at / 2)e−at
p2 /( p + a)3			(1 − 2at + a2t2 / 2)e−at
1/( p + a)4			(t3 / 6)e−at
p /( p + a)4			(t2 / 2)e−at − (at3 / 2)e−at
ω/( p	2	2	sin ωt
		+ ω )
p /( p2 + ω2 )			cos ωt
ω/[( p + a)2 + ω2 ]			e−at sin ωt
( p + a) /[( p + a)2 + ω2 ]			e−at cos ωt
1/[ p2 ( p + a)]			(1/ a2 )(e−at + at −1)
1/{ p[( p + a)2 + ω2 ]}			[1/(a2 + ω2 )][1 − e−at (cos ωt + (a / ω)sin ωt)]
p /[( p + a)( p2 + ω2 )]			[1/(a2 + ω2 )][−ae−at + a cos ωt + ωsin ωt)]
p2 /[( p + a)( p2 + ω2 )]			[1/(a2 + ω2 )][a2e−at − aωsin ωt + ω2 cos ωt)]
1/[( p + a)2 ( p + b)2 ]			1/(a −b)2	e−at (t +	2 /(a −b)) + e−bt (t − 2 /(a −b))

П.7. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ. ИНТЕГРАЛ ВЕРОЯТНОСТИ

Этот закон широко используется не только в радиотехнике [1–3, 8–11], но и практически во всех областях знаний, так как большое число различных по своей природе случайных величин имеет распределение, близкое к нормальному (рис. П.2)

	w(u) =	1	e−(u−a)2 / 2σ2 =	1	1	e−x2 / 2 =	1	w(x) ,	(П.1)
		2πσ		σ	2π
							σ
где	x = (u − a) / σ – относительное отклонение случайной величины
U ;	следовательно, u = xσ + a ;			w(x)		– плотность вероятности с
единичной дисперсией (табл. П.3).

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 3132 / 3632 33 34 35 36 > Следующая >>>

Соседние файлы в папке ТОИИТ

#
24.02.201622.54 Кб29Вопросы для экзамена по ТОИИТ.docx
#
24.02.20169.82 Mб126Задания.pdf
#
24.02.201690.11 Кб24Положение о контрольных работах зо.doc