Деление чисел в прямых кодах.

Алгоритм деления с восстановлением остаткасостоит в следующем.

1. Выполняется пробное вычитание с формированием первого остатка A₁=[Дм]_доп+[-Дм]_доп. Далее, если А₁< 0, то в первый разряд, расположенный слева от запятой заносится ноль (0, ), иначе единица (1, ) – переполнение и переход к пункту 5.

2. Если А_i< 0, то восстанавливаем предыдущий остаток A_i=A_i+[Дм]_доп.

3. Формирование очередного остатка. A_i+1=A_i∙2+[-Дм]_доп, то в очередной разряд частного справа от запятой записывается ноль (Чт(n)=0), иначе записывается единица (Чт(n)=1).

4. Если достигнута заданная точность частного или получен нулевой остаток A_i+1, то процесс деления окончен и переход к пункту 5, иначе переходим к пункту 2 алгоритма.

5. Окончание алгоритма.

Из рассмотренного алгоритма видно, что:

1) необходимо затрачивать время на восстановление остатка;

2) процесс деления не регулярный, в зависимости от делимого и делителя

частное будет содержать нулей больше или меньше, и чем больше нулей, тем больше требуется времени на восстановление остатков.

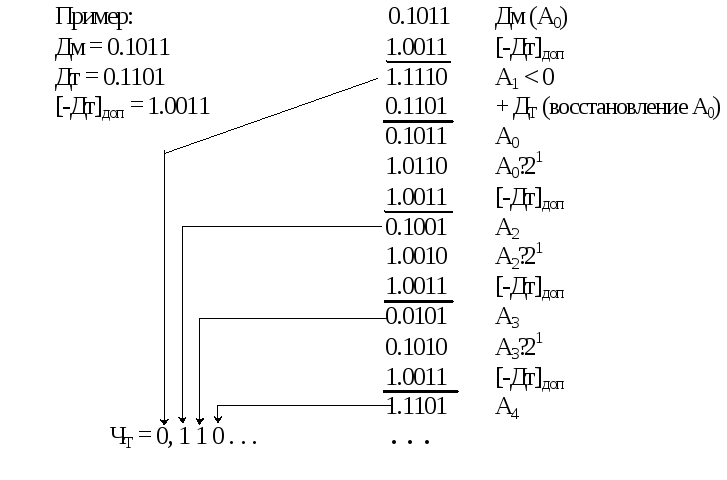
Как видно из примера, для получения остатка А_i+2необходимо выполнить

А_i+2= ( A_i+1 + Д_T) ∙ 2¹- Д_T= A_i+1∙ 2¹+ 2Д_T- Д_T= A_i+1∙ 2¹+ Д_T.

Из этого следует, что восстанавливать остаток не обязательно. Достаточно сдвинуть полученный отрицательный остаток влево на один разряд и добавить делитель. Это является основой алгоритма для выполнения деления без восстановления остатка.

Алгоритм деления без восстановленияостатка.

1. Выполняется пробное вычитание с формированием первого остатка A₁=[Дм]_доп+[-Дм]_доп. Далее, если А₁< 0, то в первый разряд, расположенный слева от запятой заносится ноль (0, ), иначе единица (1, ) – переполнение и переход к пункту 5.

2. Формирование очередного остатка. Если А_i< 0, то A_i+1=A_i∙2+[Дм]_доп, иначеA_i+1=A_i∙2+[-Дм]_доп.

3. Если А_i+1< 0, то в очередной разряд частного справа от запятой записывается ноль (Чт(n)=0), иначе записывается единица (Чт(n)=1).

4. Если достигнута заданная точность частого или получен нулевой остаток A_i+1, то процесс деления окончен и переход к пункту 5, иначе переходим к пункту 2 алгоритма.

5. Окончание алгоритма.

Деление чисел в дополнительных кодах.

При делении чисел знаковая и значащая части частного формируются раздельно. Знак частного формируется согласно формулы:

Знак Чт = Знак Дм  Знак Дт.

Основой деления чисел в дополнительных кодах является деление без восстановления остатка. В отличие от деления в прямых кодах, здесь как для определения цифры частного, так и для определения действия сравнивается знак делимого (остатка) со знаком делителя.

Ниже приведен алгоритм деления чисел в дополнительных кодах.

1. Выполняется пробное вычитание: если знак Дм знаку Дт, то первый остатокA₁=[Дм]_доп+[Дм]_доп,иначеA₁=[Дм]_доп+[-Дм]_доп. Далее формируется первый разряд, расположенный слева от запятой - ноль (0, ) если знак А₁знаку Дт, иначе единица (1, ).

2. Формирование очередного остатка. Если знак А_iзнаку Дт, то A_i+1=A_i∙2+[Дм]_доп, иначеA_i+1=A_i∙2+[-Дм]_доп.

3. Если знак А_i+1знаку Дт, то в очередной разряд частного справа от запятой заносится ноль (Чт(n)=0), иначе единица (Чт(n)=1).

4. Если достигнута заданная точность частого или получен нулевой остаток A_i+1, то процесс деления окончен, иначе переходим к пункту 2 алгоритма.

Пример: Дм = - 0.1011 [ Дм ]_доп = 1.0101

Дт = 0.1101 [ Дт ]_доп = 0.1101 [-Дт ]_доп = 1.0011

На деление Дм и Дтпридут в дополнительном коде