
- •Арифметические и логические основы вычислительной техники учебное пособие
- •Введение
- •Арифметические основы вычислительной техники Системы счисления
- •Двоичная система счисления
- •Восьмеричная система счисления
- •Шестнадцатеричная система счисления
- •Критерии выбора системы счисления
- •Перевод чисел из одной системы счисления в другую
- •Перевод целых чисел.
- •Перевод правильных дробей.
- •Перевод чисел из системы счисления в систему счисления основания которых кратны степени 2
- •Кодирование чисел
- •Переполнение разрядной сетки
- •Модифицированные коды
- •Машинные формы представления чисел.
- •Погрешность выполнения арифметических операций
- •Округление
- •Нормализация чисел
- •Последовательное и параллельное сложение чисел
- •Сложение чисел с плавающей запятой
- •Машинные методы умножения чисел в прямых кодах
- •Ускорение операции умножения
- •Умножение с хранением переносов
- •Умножение на два разряда множителя одновременно.
- •Умножение на четыре разряда одновременно.
- •Умножение в дополнительных кодах.
- •Умножение на 2 разряда Мт в дополнительных кодах.
- •Матричные методы умножения.
- •Машинные методы деления
- •Деление чисел в прямых кодах.
- •Деление чисел в дополнительных кодах.
- •Методы ускорения деления.
- •Двоично-десятичные коды
- •Суммирование чисел с одинаковыми знаками в коде 8421.
- •Сложение чисел с разными знаками.
- •Двоично-десятичные коды с избытком 3
- •Код с избытком 6 для одного из слагаемых
- •Система счисления в остаточных классах (сок)
- •Представление отрицательных чисел в сок
- •Контроль работы цифрового автомата
- •Некоторые понятия теории кодирования
- •Обнаружение и исправление одиночных ошибок путем использования дополнительных разрядов
- •Коды Хемминга
- •Логические основы вычислительной техники Двоичные переменные и булевы функции
- •Способы задания булевых функций
- •Основные понятия алгебры логики
- •Основные законы алгебры логики
- •Формы представления функций алгебры логики
- •Системы функций алгебры логики
- •Минимизация фал
- •Метод Квайна
- •Метод Блейка - Порецкого
- •Метод минимизирующих карт Карно (Вейча)
- •Б) в) Рис. 19 Таблица истинности и карта Карно
- •Минимизация коньюнктивных нормальных форм.
- •Минимизация не полностью определенных фал
- •Кубическое задание функций алгебры логики.
- •Метод Квайна-Мак Класки
- •Алгоритм извлечения (Рота)
- •Минимизация фал методом преобразования логических выражений
- •Применение правил и законов алгебры логики к синтезу некоторых цифровых устройств Синтез одноразрядного полного комбинационного сумматора
- •Синтез одноразрядного комбинационного полусумматора
- •Синтез одноразрядного полного комбинационного сумматора на двух полусумматорах
- •Синтез одноразрядного комбинационного вычитателя
- •Объединенная схема одноразрядного комбинационного сумматора-вычитателя
- •Триггер со счетным входом как полный одноразрядный сумматор
- •Введение в теорию конечных автоматов Основные понятия теории автоматов
- •Способы задания автоматов
- •Структурный автомат
- •Память автомата
- •Канонический метод синтеза
- •Пример синтеза мпа Мили по гса
- •Синхронизация автоматов
- •Литература
- •220013, Минск, п.Бровки, 6.
Умножение на 2 разряда Мт в дополнительных кодах.
i i+1 i i+1 00 11 00 10 01 01 01 10 +4MH -MH +4MH -2MH
Таблица 2.
-
I ая пара
i+1ая пара
Преобраз. Пара
Алгоритм
х
y
z
x’
y’
A
Г
0
0
0
0
0
1
6
0
0
1
0
1
2
7
0
1
0
0
1
2
7
0
1
1
1
0
3
8
 1
10
0
1
0
4
9
 1
10
1
0
1
5
10
 1
11
0
0
1
5
10
1
1
1
0
0
1
6
В табл. 2 приведены преобразования i и i+1 пары МT.действия, осущестляемые при выполнении, например, алгоритмов А и Г.
(1)
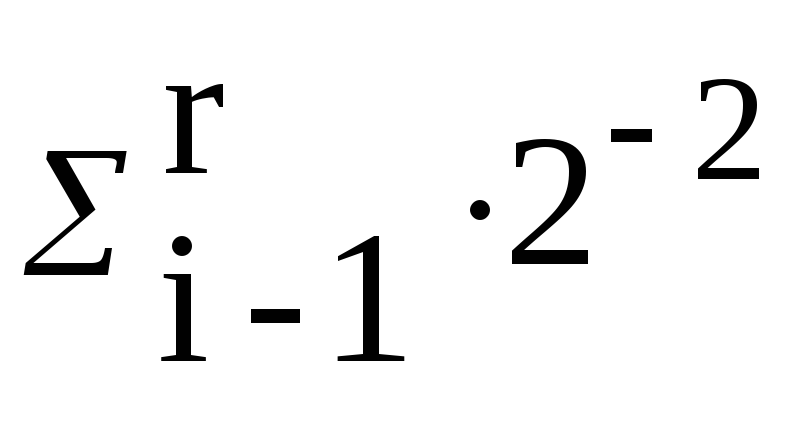 (6)
(6)
![]()
(2)
 (7)
(7)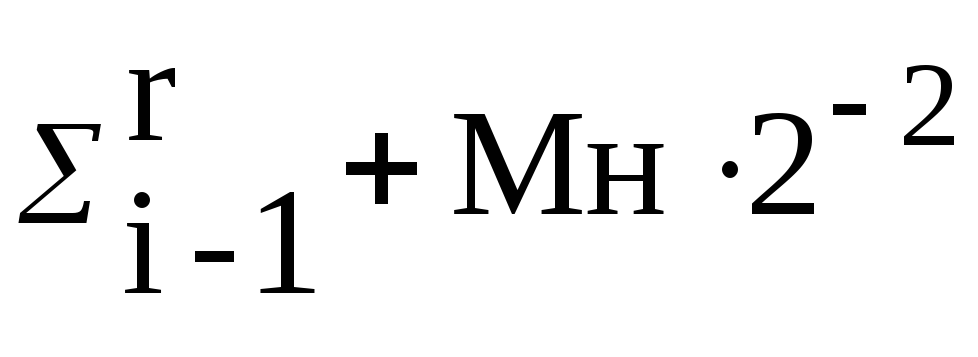
(3)
 (8)
(8)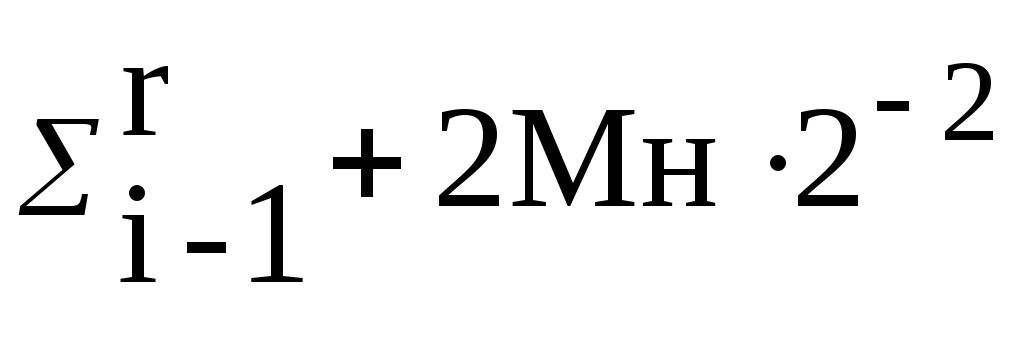
(4)
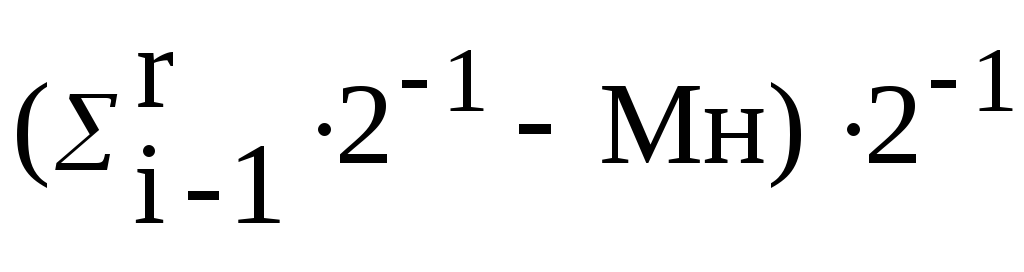 (9)
(9)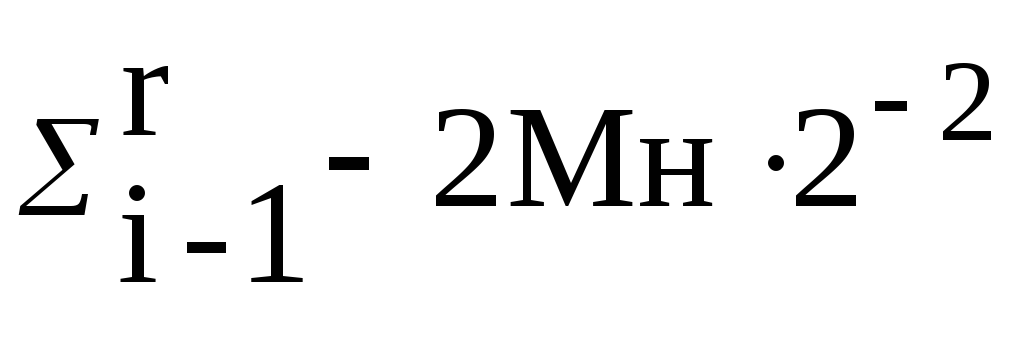
(5)
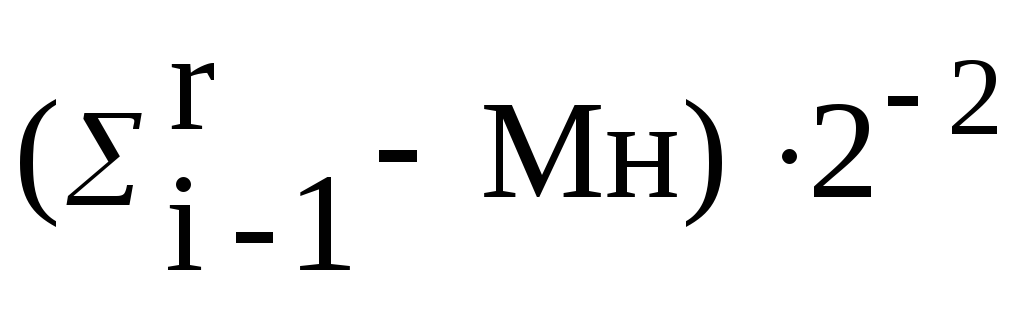 (10)
(10)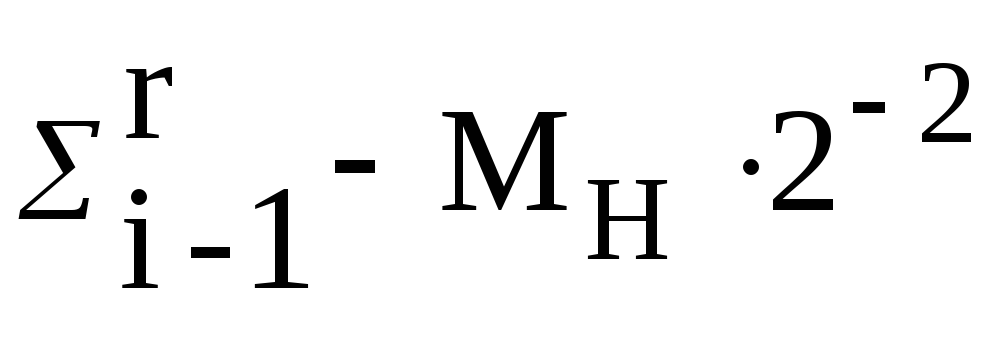
Если i+1 пара имеет старшую цифру 1, то умножение на эту пару будет соответствовать вычитанию одного или двух множителей.
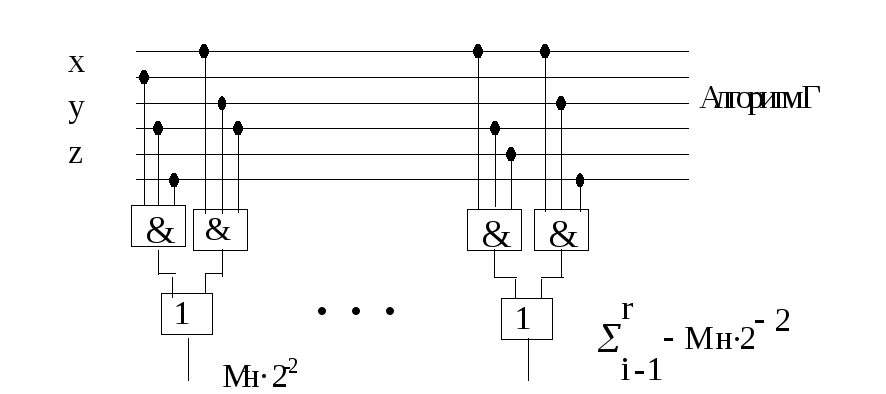
Рис. 9. Логическая схема формирования сигнала сдвига частичной суммы.
Как было показано выше, при умножении чисел в дополнительных кодах в общем случае необходимо вводить поправку для получения верного произведения. Однако при умножении на два разряда множителя этого выполнять не требуется. Если на умножение приходит отрицательный множитель, то при преобразовании его старшей пары происходит формирование дополнительной пары:
Мт = -10110
[Мт]доп= 1.0 10 10
[



 Мт]допп=
01 01 01 10
Мт]допп=
01 01 01 10
П ри
умножении на дополнительную пару (01)
происходит вычитание одного множителя
, а затем он должен быть добавлен в
качестве поправки. Таким образом тратится
два такта на выполнение взаимноисключающих
операций.
ри
умножении на дополнительную пару (01)
происходит вычитание одного множителя
, а затем он должен быть добавлен в
качестве поправки. Таким образом тратится
два такта на выполнение взаимноисключающих
операций.
Пример:
Мн = + 0101 умножение выполним согласно
MT = + 1100111 алгоритма Г.
[MH]доп = 0.0101
[MT]доп = 0.1 10 01 11
Анализ пар МTможно производить, начиная от старших (при умножении по алгоритмам В и Г) и от младших разрядов (алгоритмы А и Б).
![]()

 =
10 10 10 01
=
10 10 10 01
[-2Mн]доп = 1.0110 [2Mн]доп = 0.1010
0.0000
00000000 ![]()
0.0010
10000000 ![]() = 2MH∙2-2
= 2MH∙2-2
0.0010
10000000 ![]()
1.1111
01100000 ![]() =
-2MH∙2-4
=
-2MH∙2-4
0.0001
11100000 ![]()
0.0000
00101000
![]() = 2MH∙2-6
= 2MH∙2-6
0.0010
00001000 ![]()
1.1111
11111011
![]() = -MH∙2-8
= -MH∙2-8
0.0010
00000011 ![]() =
[Mн Mт]доп
=
[Mн Mт]доп
Пример:
Mн= - 0101 умножение выполним согласно
Mт = -1100111 алгоритма Б.
[Mн]доп = 1.1011
[Mт]доп = 1.0 01 10 01


![]() = 1.0 10 10 01
= 1.0 10 10 01
[2Mн]доп = 1.0110 [-2Mн]доп = 0.1010
0.000000
0000 ![]()
1.111111
1011 ![]() =
MH
=
MH
1.111111
1011 ![]()
0.000010
1000 ![]() =
-2MH ∙
22
=
-2MH ∙
22
0.000010
0011 ![]()
1.110110
0000 ![]() =
2MH ∙
24
=
2MH ∙
24
1.111000
0011 ![]()
0.101000
0000 ![]() = -2MH ∙
26
= -2MH ∙
26
0.100000
0011 ![]() =MH
MT
=MH
MT
