
- •10 Дифракция Фраунгофера на дифракционной решетке.
- •11 Понятие о голографии.
- •14. Многолучевая интерференция света.
- •15. Проблемы излучения черного тела. Закон Кирхгофа.
- •16 Закон Стефана - Больцмана.
- •17. Квантовая гипотеза Планка. Энергия и импульс световых квантов.
- •18. Внешний фотоэффект.
- •19 Гипотеза де Бройля.
- •22. Дифракция электронов.
- •23. Волновая функция микрочастицы: её основные свойства и статистический смысл.
- •24. Нестационарное уравнение Шрёдингера.
- •25. Уравнение Шрёдингера для стационарных состояний.
- •26. Волновые функции частицы в одномерной прямоугольной яме.
- •27. Квантование энергии частицы в одномерной прямоугольной яме.
- •28. Волновые функции частицы при туннельном эффекте.
- •29. Коэффициент прозрачности в туннельном эффекте.
- •30. Структура уровней атома водорода.
- •31. Главное, орбитальное, магнитное, спиновые числа для волновых функций частиц
- •32. Принцип Паули. Распределение электронов в атоме по состояниям.
- •33. Понятие о квантовой статистике Бозе-Эйнштейна. Понятие о квантовой статистике Ферми-Дирака.
- •34. Влияние температуры на распределение электронов. Уровень Ферми
- •35. Зависимость сопротивления полупроводника от температуры. Уровень Ферми.
- •36 Строение атомного ядра и его характеристики
- •37 Понятие о свойствах и природе ядерных сил.
- •38 Виды радиоактивных превращений атомных ядер
- •39. Статистический закон распада атомных ядер
- •40 Реакция ядерного деления
1 Когерентность и монохроматичность световых волн.
Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны - не ограниченные в пространстве волны одной определенной и строго постоянной частоты. Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Поэтому на опыте не наблюдается интерференция света от независимых источников, например от двух электрических лампочек.
2 Время и длина когерентности световой волны
Если волна распространяется в однородной среде, то фаза колебаний в определен ной точке пространства сохраняется только в течение времени когерентности tког. За это время волна распространяется в вакууме на расстояние lког = ctког, называемое длиной когерентности (или длиной цуга). Таким образом, длина когерентности есть расстояние, при прохождении которого две или несколько волн утрачивают когерентность. Отсюда следует, что наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для используемого источника света.
Чем ближе волна к монохроматической, тем меньше ширина Dw спектра ее частот и, как можно показать, больше ее время когерентности tког, следовательно, и длина когерентности lког. Когерентность колебаний, которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности волн, называется временной когерентностью.
3 Сложение интенсивностей световых волн при интерференции.
две монохроматические световые волны, накладываюсь друг на друга, возбуждают в определенной точке пространства колебания одинакового направления: х1 = А1cos(wt + j1) и x2 = A2cos(wt + j2). Под х понимают напряженность электрического Е или магнитного Н полей волны; векторы Е и Н колеблются во взаимно перпендикулярных плоскостях. Напряженности электрического и магнитного полей подчиняются принципу суперпозиции. Амплитуда результирующего колебания в данной точке A2 = A2l + A22 + 2A1A2 cos(j2 - j1) (см. 144.2)). Так как волны когерентны, то cos(j2 - j1) имеет постоянное во времени (но свое для каждой точки пространства) значение, поэтому интенсивность результирующей волны (1~А2)
![]()
В точках пространства, где cos(j2 - j1) > 0, интенсивность I > I1 + I2 , где cos(j2 - j1) < О, интенсивность I < I1 + I2. Следовательно, при наложении двух (или нескольких) когерентных световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других - минимумы интенсивности. Это явление называется интерференцией света.
Для некогерентных волн разность (j2 - j1) непрерывно изменяется, поэтому среднее во времени значение cos(j2 - j1) равно нулю, и интенсивность результирующей волны всюду одинакова и при I1 = I2 равна 2I1 (для когерентных волн при данном условии в максимумах I = 4I1 в минимумах I = 0).
4 Расчет интерференционной картины от двух когерентных источников.
Расчет интерференционной картины от двух источников можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу:
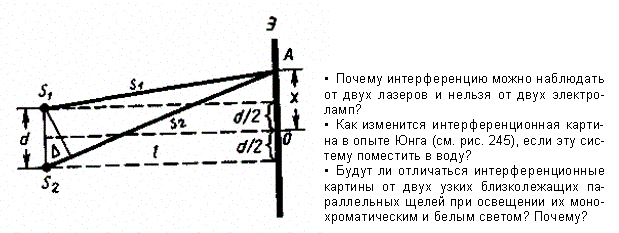
Щели S1 и S2 находятся на расстоянии d друг от друга и являются когерентными (реальными или мнимыми изображениями источника S в какой-то оптической системе) источниками света. Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l≫d. Начало отсчета выбрано в точке О, симметричной относительно щелей.
Интенсивность в любой точке А экрана, лежащей на расстоянии х от О, определяется оптической разностью хода D = s2 – s1
![]()
откуда s22 - s21 = 2xd, или
![]()
Из условия l≫d следует, что s1 + s2 » 2l, поэтому
![]()
максимумы интенсивности будут наблюдаться в случае, если
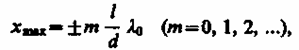
а минимумы -- в случае, если
![]()
Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равно
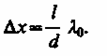
5 Кольца Ньютона.
Кольца Ньютона, являющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис. 252). Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падении света имеющие вид концентрических окружностей.
В отраженном свете оптическая разность хода (с учетом потери полуволны при отражении), согласно (174.1), при условии, что показатель преломления воздуха n = 1, а I = 0,
![]()
где d-ширина зазора.
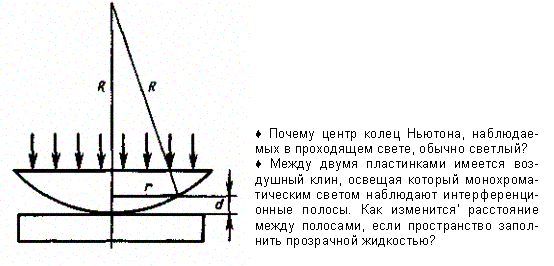
Из рис. 252 следует, что R2 = (R - d)2 + r2, где R - радиус кривизны линзы, r - радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая, что d мало, получим d = r2/(2R). Следовательно,
![]()
Приравняв (174.4) к условиям максимума (172.2) и минимума (172.3), получим выражения для радиусов m-гo светлого кольца и m-го темного кольца соответственно
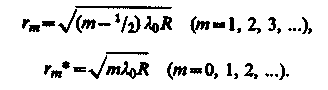
Измеряя радиусы соответствующих колец, можно (зная радиус кривизны линзы R) определить l0 и, наоборот, по известной l0 найти радиус кривизны R линзы.
6 Просветление оптики
на свободные поверхности линз наносят тонкие пленки с показателем преломления, меньшим, чем у материала линзы. При отражении света от границ раздела воздух - пленка и пленка - стекло возникает интерференция когерентных лучей 1¢ и 2'
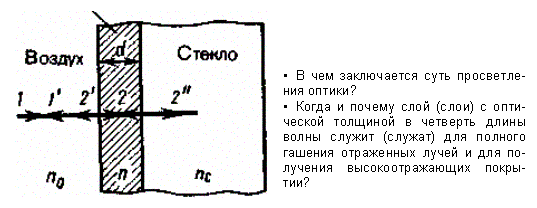
Толщину пленки d и показатели преломления стекла nс и пленки n можно подобрать так, чтобы волны, отраженные от обеих поверхностей пленки, гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность хода равна - (см. (172.3)). Расчет показывает, что амплитуды отраженных лучей равны, если
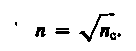
Так как nс, n и показатель преломления воздуха n0 удовлетворяют условиям nс > n > n0, то потеря полуволны происходит на обеих поверхностях; следовательно, условие минимума (предполагаем, что свет падает нормально, т. е. I = 0)
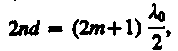
где nd - оптическая толщина пленки. Обычно принимают m = 0, тогда
![]()
Таким образом, если выполняется условие (175.1) и оптическая толщина пленки равна l0/4, то в результате интерференции наблюдается гашение отраженных лучей. Так как добиться одновременного гашения для всех длин волн невозможно, то это обычно делается для наиболее восприимчивой глазом длины волны l0 » 0,55 мкм. Поэтому объективы с просветленной оптикой имеют синевато-красный оттенок.
7 Принцип Гюйгенса-Френеля. Метод зон Френеля.
1 Окружим все источники света S1, S2 , S3… произвольной замкнутой поверхностью F (рис.5.2.1.) Каждую точку такой поверхности можно рассматривать как источник вторичных волн, распространяющихся во всех направлениях. Эти волны когерентны, поскольку все они возбуждаются одними и теми же первичными источниками. Световое поле, возникающее в результате их интерференции, в пространстве вне их интерференции, в пространстве вне поверхности F совпадает с полем реальных источников света.
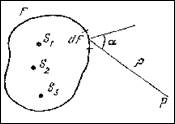
Таким образом, действительные источники света можно как бы заменить окружающей их светящейся поверхностью F с непрерывно распределёнными по ней когерентными вторичными источниками. Отличие этой поверхности от реальной поверхности излучающего тела состоит в том, что она абсолютно прозрачна для всего излучения. В такой формулировке принцип Гюйгенса-Френеля выражает весьма общее положение. Он означает, что волна, отделившаяся от своих источников, в дальнейшем ведет автономное существование, совершенно не зависящее от наличия источников.
2 Вычисления результата интерференции вторичных волн очень упрощается, если применить следующий указанный Френелем прием: для вычисления действия в точке В соединяем А с В и разбиваем поверхность S на зоны такого размера, чтобы расстояния от краев зоны до В отличались на ½ l, т.е.
М1В-М0В=М2В-М1В=М3В-М2В=…= ½ l
Нетрудно вычислить размеры полученных таким образом зон. Из рис. 5.2.3 получаем для первой зоны
![]()
Так как l очень мало по сравнению с а или b, то
![]()
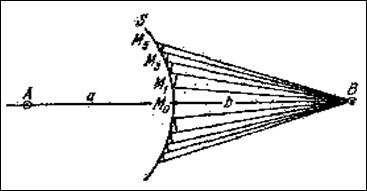
И, следовательно, площадь сферического сегмента, представляющего первую зону,
![]()
Практически
ту же площадь будет иметь и каждая из
всех последующих зон. Таким образом,
построение Френеля разбивает поверхность
сферической волны на равновеликие зоны,
каждая из которых имеет площадь
![]()
8 Дифракция Френеля на круглом отверстии и диске.
Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259). Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами
![]()
где знак плюс соответствует нечетным m и минус — четным m.

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А=А1, т. е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если m нечетное — то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.
Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то Аm<<A1 и результирующая амплитуда A=A1/2, т. е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблюдается, свет распространяется, как и в отсутствие круглого отверстия, прямолинейно.
2. Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром диска (рис. 260). В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна
![]()
Или
![]()
так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.
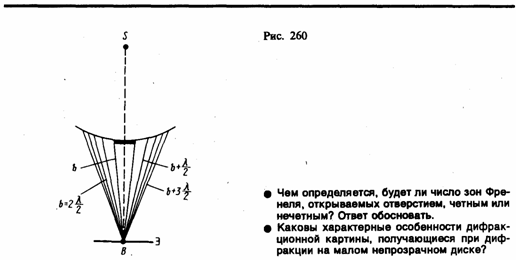
С увеличением радиуса диска первая открытая зона Френеля удаляется от точки В и увеличивается угол jт (см. рис. 258) между нормалью к поверхности этой зоны и направлением на точку В. В результате интенсивность центрального максимума с увеличением размеров диска уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место весьма слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распространяющимся прямолинейно.
9 Дифракция Фраунгофера на одной щели.
Пусть в непрерывном экране есть щель: ширина щели , длина щели (перпендикулярно плоскости листа) (рис. 9.5). На щель падают параллельные лучи света. Для облегчения расчета считаем, что в плоскости щели АВ амплитуды и фазы падающих волн одинаковы.
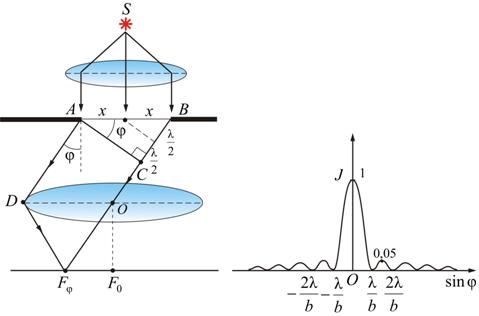 Разобьем
щель на зоны Френеля так, чтобы оптическая
разность хода между лучами, идущими от
соседних зон, была равна
Разобьем
щель на зоны Френеля так, чтобы оптическая
разность хода между лучами, идущими от
соседних зон, была равна
![]() .
.
Если
на ширине щели укладывается четное
число таких зон, то в точке
![]() (побочный фокус линзы) будет наблюдаться
минимум интенсивности, а если нечетное
число зон, то максимум интенсивности:
(побочный фокус линзы) будет наблюдаться
минимум интенсивности, а если нечетное
число зон, то максимум интенсивности:
![]() –условие
минимума интенсивности;
–условие
минимума интенсивности;
![]() –условие
максимума интенсивности
–условие
максимума интенсивности
Картина
будет симметричной относительно главного
фокуса точки
![]() .
Знак плюс и минус соответствует углам,
отсчитанным в ту или иную сторону.
.
Знак плюс и минус соответствует углам,
отсчитанным в ту или иную сторону.
При уменьшении ширины щели b вся картина расширяется, расплывается, центральная полоска тоже расширяется, захватывая все большую часть экрана, а интенсивность ее уменьшается.
10 Дифракция Фраунгофера на дифракционной решетке.
Одномерная дифракционная решетка представляет собой систему из большого числа N одинаковых по ширине и параллельных друг другу щелей в экране, разделенных также одинаковыми по ширине непрозрачными промежутками
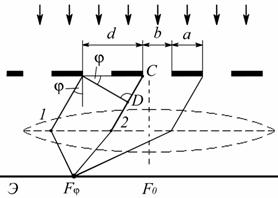
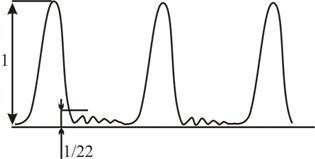
Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.
Обозначим: b – ширина щели решетки; а – расстояние между щелями; a+b=d – постоянная дифракционной решетки.
Пусть
луч 1 падает на линзу под углом φ
(угол дифракции). Световая волна, идущая
под этим углом от щели, создает в точке
![]() максимум интенсивности. Второй луч,
идущий от соседней щели под этим же
угломφ,
придет в ту же точку
максимум интенсивности. Второй луч,
идущий от соседней щели под этим же
угломφ,
придет в ту же точку
![]() . Оба эти луча придут в фазе и будут
усиливать друг друга, если оптическая
разность хода будет равнаmλ:
. Оба эти луча придут в фазе и будут
усиливать друг друга, если оптическая
разность хода будет равнаmλ:
![]()
Условие максимума для дифракционной решетки будет иметь вид:
![]()
где m = ± 1, ± 2, ± 3, … .
Максимумы, соответствующие этому условию, называются главными максимумами. Значение величины m, соответствующее тому или иному максимуму называется порядком дифракционного максимума.
В точке F0 всегда будет наблюдаться нулевой или центральный дифракционный максимум.
Так как свет, падающий на экран, проходит только через щели в дифракционной решетке, то условие минимума для щели и будет условием главного дифракционного минимума для решетки:
![]()
11 Понятие о голографии.
Голография (от греч. «полная запись») - особый способ записи и последующего восстановления волнового поля, основанный на регистрации интерференционной кар тины. Она обязана своим возникновением законам волновой оптики - законам интерференции и дифракции.
Этот принципиально новый способ фиксирования и воспроизведения пространственного изображения предметов изобретен английским физиком Д. Табором (1900-1979) в 1947 г. (Нобелевская премия 1971 г.). Экспериментальное воплощение и дальнейшая разработка этого способа (Ю. Н. Денисюком в 1962 г. и американскими физиками Э. Лейтом и Ю. Упатниексом в 1963 г.) стали возможными после появления в 1960 г. источников света высокой степени когерентности - лазеров (см. § 233).
Рассмотрим элементарные основы принципа голографии, т. е. регистрации и восстановления информации о предмете. Для регистрации и восстановления волны необходимо уметь регистрировать и восстанавливать амплитуду и фазу идущей от предмета волны.
для регистрации как фазовой, так и амплитудной информации кроме волны, идущей от предмета (так называемой предметной волны), используют еще когерентную с ней волну, идущую от источника света (так называемую опорную волну). Идея голографирования состоит в том, что фотографируется распределение интенсивности в интерференционной картине, возникающей при суперпозиции волнового поля объекта и когерентной ему опорной волны известной фазы. Последующая дифракция света на зарегистрированном распределении почернений в фотослое восстанавливает волновое поле объекта и допускает изучение этого поля при отсутствии объекта.
Обычно пользуются мнимым топографическим изображением, которое по зритель ному восприятию создает полную иллюзию существования реального предмета. Рассматривая из разных положений объемное изображение предмета, даваемое голограммой, можно увидеть более удаленные предметы, закрытые более близкими из них (заглянуть за ближние предметы). Это объясняется тем, что, перемещая голову в сторону, мы воспринимаем изображение, восстановленное от периферической части голограммы, на которую при экспонировании падали также и лучи, отраженные от скрытых предметов. Голограмму можно расколоть на несколько кусков. Но даже малая часть голограммы восстанавливает полное изображение. Однако уменьшение размеров голо граммы приводит к ухудшению четкости получаемого изображения. Это объясняется тем, что голограмма для опорного пучка служит дифракционной решеткой, а при уменьшении числа штрихов дифракционной решетки (при уменьшении размеров голограммы) ее разрешающая способность уменьшается.
Методы голографии (запись голограммы в трехмерных средах, цветное и панорамное голографирование и т. д.) находят все большее развитие. Применения голографии разнообразны, во наиболее важными, приобретающими все большее значение, являются запись и хранение информации. Методы голографии позволяют записывать в сотни раз больше страниц печатного текста, чем методы обычной микрофотографии. По подсчетам, на фотопластинку размером 32´32 мм можно записать 1024 голограммы (площадь каждой из них 1 мм2), т. е. на одной фотопластинке можно «разместить» книгу объемом свыше тысячи страниц. В качестве будущих разработок могут служить ЭВМ с топографической памятью, голографический электронный микроскоп, голографические кино и телевидение, топографическая интерферометрия и т. д.
12 Естественный и поляризованный свет. Циркулярно- и плоско-поляризаванный свет. Степень поляризация света.
Свет наз. естественным или неполяризованным, если направление колебания вектора Е не является преимущественным. Свет называется частично поляризованным, если в нем имеется преимущественные направление колебания вектора Е. Частично поляриз. свет можно рассматривать как совокупность одновременно распространяющихся в одном и том же направлении естественного и линейно поляризованного света. Поляризацией света назыв. выделение линейно поляризованного света из естественного или частично поляризованного. Для этой цели используют поляризаторы. Их действие основывается на поляризации света при его отражении и преломлении на границе раздела двух сред, а также на явлениях линейного лучепреломления и дихроизма. То же устройство можно использовать в качестве анализаторов, т.е. для определения характера и степени поляризации света.
Циркулярно поляризованный свет - это частный случай эллиптически поляризованного света.
В циркулярно поляризованном свете компонента электрического поля изменяется по направлению таким образом, что электрическое поле при движении по оси распространения света описывает спираль, отвечающую движению либо по часовой стрелке, либо против нее.
Плоскополяризованный свет получают с помощью двоякопреломляющих кристаллов. Для этого достаточно один из поляризованных лучей каким-нибудь образом погасить, тогда другой луч даст полностью поляризованный свет.
Степень поляризации тем выше, чем меньше размеры частиц, на которых происходит рассеяние.
13 Поляризация света при отражении. Законы Малюса и Брюстера.
Если угол падения света на границу раздела двух диэлектриков (например, на поверхность стеклянной пластинки) отличен от нуля, отраженный и преломленный лучи оказывают частично поляризован-ными.
Причем, при отражении от проводящей поверхности (например, от поверхности металла) получается эллиптически-поляризованный свет. Степень поляриза-ции зависит от угла падения.
Закон Малюса — зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла между плоскостями поляризации падающего света и поляризатора.
Закон Брюстера — закон оптики, выражающий связь показателя преломления с таким углом, при котором свет, отражённый от границы раздела, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения, а преломлённый луч частично поляризуется в плоскости падения, причем поляризация преломленного луча достигает наибольшего значения. Легко установить, что в этом случае отраженный и преломленный лучи взаимно перпендикулярны. Соответствующий угол называется углом Брюстера.

