25. Уравнение Шрёдингера для стационарных состояний.

Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда не является функцией времени, можно записать в виде:

где функция должна удовлетворять уравнению:

которое получается из уравнения Шрёдингера (1) при подстановке в него указанной выше формулы для (2). Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени).

26. Волновые функции частицы в одномерной прямоугольной яме.

Графики волновых функций для первых четырех значений квантового числа n приведены на рис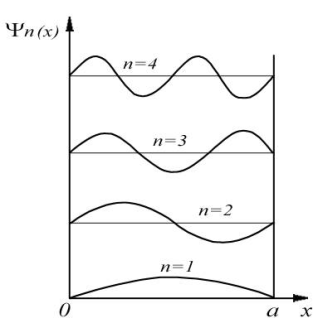Волновые функции, отвечающие разным значениямn , существенно отличаются друг от друга. Если поместить начало координат в середину ямы, то волновые функции частицы внутри ямы для нечетных значений n будут четными функциями координаты x , и наоборот, волновые функции для четных n - нечетными функциями координаты. При увеличении квантового числа n на единицу число точек пересечения волновой функции с осью x также увеличивается на единицу. Отличительным свойством найденных волновых функций является излом, т.е. скачок производной на границах ямы. Этот скачок возникает вследствие того, что на границах ямы потенциальная энергия частицы u (x) обращается в бесконечность. В случае ямы конечной глубины, как показано в разделе 4.4 , скачок производной волновой функции на границе ямы отсутствует, т.е. волновая функция является гладкой.

27. Квантование энергии частицы в одномерной прямоугольной яме.

Решение уравнения Шредингера само по себе к квантованию энергии не приводит, квантование возникает из-за граничных условий, накладываемых на волновую функцию, т.е. из-за равенства нулю волновой функции на границе потенциальной ямы.

Число n , определяющее энергию частицы в яме, называется квантовым числом, а соответствующее ему значение En - уровнем энергии. Состояние частицы с наименьшей энергией, в данном случае с n=1 , называется основным состоянием. Все остальные состояния являются возбужденными: значение n=2 отвечает первому возбужденному состоянию, значениеn=3 - второму возбужденному состоянию и т.д.

28. Волновые функции частицы при туннельном эффекте.

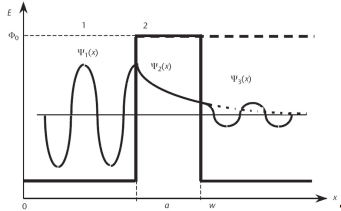Волновая функция в случае, если энергия частицы меньше высоты барьера.

туннельный эффект, который заключается в проникновении легких частиц (электрона, протона) в области, недоступные для них энергетически. Этот эффект играет важную роль в таких процессах как например перенос заряда в фотосинтетических устройствах живых организмов (стоит заметить, что биологические реакционные центры являются одними из наиболее эффективных наноструктур).

29. Коэффициент прозрачности в туннельном эффекте.

Туннельный эффект принято характеризовать так называемым коэффициентом прозрачности барьера:

Коэффициент прозрачности характеризует вероятность прохождения частицы сквозь барьер. Эта вероятность очень сильно зависит от толщины барьера d: чем толще барьер, тем меньше вероятность туннельного эффекта. Туннельный эффект используется в электронике (туннельные диоды, автоэлектронная эмиссия). Природа a -распада также связана с туннельным эффектом.