ЦОС 1лб
..docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ»
ИНСТИТУТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
ФАКУЛЬТЕТ КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ
ЛАБОРАТОРНАЯ РАБОТА №1 ПО ТЕМЕ
«ПРИМЕНЕНИЕ ДИСКРЕТНЫХ ОРТОГОНАЛЬНЫХ ПРЕОБРАЗОВАНИЙ»
ЧАСТЬ 1
ВЫПОЛНИЛ:
СТУДЕНТ ГРУППЫ 380562
Петров Н.А.
ПРОВЕРИЛ:
ПРЕПОДАВАТЕЛЬ
МИТЮХИН А.И.
МИНСК 2015
1. Цель работы
Изучение свойств дискретных ортогональных преобразований и их применение в цифровой обработке сигналов и изображений.
2. Краткие теоретические сведения
Модели сигналов в виде функции времени предназначены, в первую очередь, для анализа формы сигналов. При решении задач прохождения сигналов сложной формы через какие-либо устройства такая модель сигнала часто не совсем удобна и не позволяет понять суть происходящих в устройствах физических процессов.
Поэтому сигналы представляют набором элементарных (базисных) функций, в качестве которых наиболее часто используют ортогональные гармонические (синусоидальные и косинусоидальные) функции. Выбор именно таких функций обусловлен тем, что они являются, с математической точки зрения, собственными функциями инвариантных во времени линейных систем (систем, параметры которых не зависят от времени), т.е. не изменяют своей формы после прохождения через эти системы. В результате сигнал может быть представлен множеством амплитуд, фаз и частот гармонических функций, совокупность которых называется спектром сигнала.
Таким
образом, существуют две формы представления
произвольного детерминированного
сигнала:
временное
и частотное (спектральное). Первая форма
представления основана на математической
модели сигнала в виде функции времени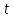 :
:
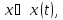
вторая
– на математической модели сигнала в
виде функции частоты
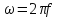 ,
причем
эта модель существует только в области
комплексных функций:
,
причем
эта модель существует только в области
комплексных функций:
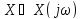 .
.
Обе формы представления сигнала связаны между собой парой преобразований Фурье:
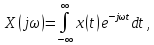 (2.1)
(2.1)
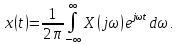 (2.2)
(2.2)

При
использовании линейной частоты
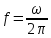 преобразования Фурье имеют следующий
вид:
преобразования Фурье имеют следующий
вид:
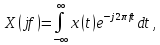 (2.3)
(2.3)
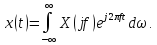 (2.4)
(2.4)
Из формул (2.2), (2.4) следует, что любой сложный периодический сигнал может быть представлен в виде суммы гармонических колебаний с частотами, кратными основной частоте.
Теория
цифровой обработки сигналов связана с
описанием и обработкой временных и
частотных последовательностей. Пусть
задана произвольная временная дискретная
последовательность
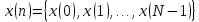 .
Такая числовая последовательность
может быть представлена как сумма
взвешенных и задержанных цифровых
единичных импульсов. Цифровой единичный
импульс (отсчёт), определяется следующим
образом:
.
Такая числовая последовательность
может быть представлена как сумма
взвешенных и задержанных цифровых
единичных импульсов. Цифровой единичный
импульс (отсчёт), определяется следующим
образом:
 (2.5)
(2.5)
где
𝑛
= 0,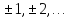
3. Предварительное задание
3.1
Вычислить значения ДЭФ:
 ,
,
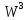 ,
,
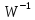
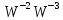 при
при
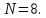
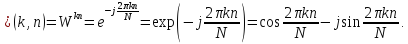
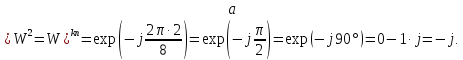

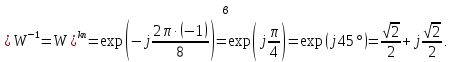
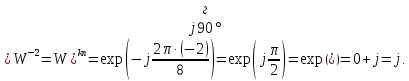
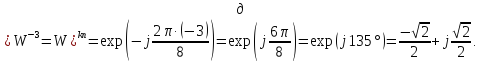
3.2
Функции системы ДЭФ записать в виде
матрицы
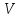 размерностью
размерностью
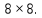
Систему
ДЭФ записывают в виде матрицы
 строки которой нумеруются переменной
строки которой нумеруются переменной
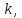 столбцы переменной
столбцы переменной
 .
В пересечении k-й
строки и -го столбца записывается
величина
.
В пересечении k-й
строки и -го столбца записывается
величина
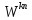 ,
для
,
для
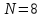 матрица
матрица
 имеет следующий вид:
имеет следующий вид:
|
V = |
|
W 0 |
W 0 |
W 0 |
W 0 |
W 0 |
W 0 |
W 0 |
W 0 |
|
|
W 0 |
W 1 |
W 2 |
W 3 |
W 4 |
W 5 |
W 6 |
W 7 |
|||
|
W 0 |
W 2 |
W 4 |
W 6 |
W 8 |
W 10 |
W 12 |
W 14 |
|||
|
W 0 |
W 3 |
W 6 |
W 9 |
W 12 |
W 15 |
W 18 |
W 21 |
|||
|
W 0 |
W 4 |
W 8 |
W 12 |
W 16 |
W 20 |
W 24 |
W 28 |
|||
|
W 0 |
W 5 |
W 10 |
W 15 |
W 20 |
W 25 |
W 30 |
W 35 |
|||
|
W 0 |
W 6 |
W 12 |
W 18 |
W 24 |
W 30 |
W 36 |
W 42 |
|||
|
W 0 |
W 7 |
W 14 |
W 21 |
W 28 |
W 35 |
W 42 |
W 49 |
Произведем расчёт от W0 до W7, оставшиеся значения найдем из свойства периодичности:
|
|
|
|
|
|
|
|
|
|
|
|
Заполним исходную матрицу V:
|
V = |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
1 |
|
|
|
-1 |
|
|
|
|||
|
1 |
|
-1 |
|
1 |
|
-1 |
|
|||
|
1 |
|
|
|
-1 |
|
|
|
|||
|
1 |
-1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
|||
|
1 |
|
|
|
-1 |
|
|
|
|||
|
1 |
|
-1 |
|
1 |
|
-1 |
|
|||
|
1 |
|
|
|
-1 |
|
|
|
3.3 Вычислить спектр дискретизированного сигнала, показанного на рисунке 3.1, с помощью ДПФ. Построить графики амплитудного и фазового спектров.
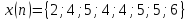 ,
,
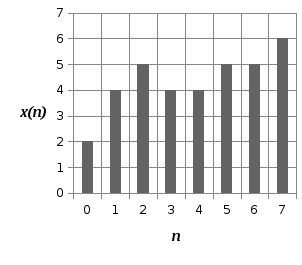
Рисунок 3.1 – Дискретизированный сигнал
Произведем расчёт дискретной последовательности в частотной области:
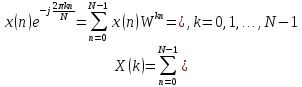
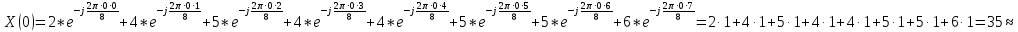 1,41
1,41
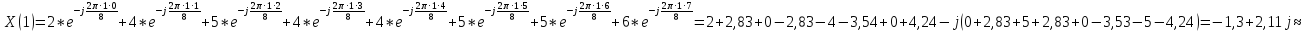 1
1
,41
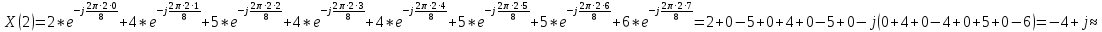 1,41
1,41
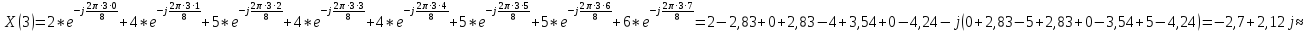 1,41
1,41
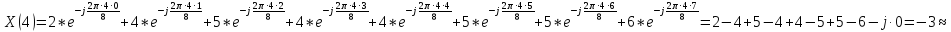 1,41
1,41
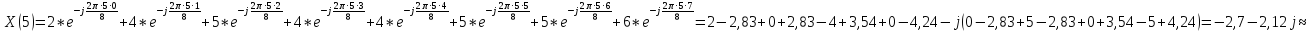 1,41
1,41
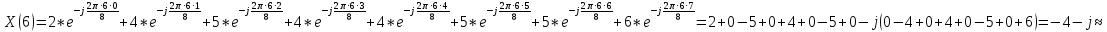 1,41
1,41
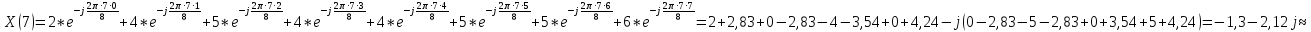 1
1
,Совокупность
значений
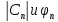 называется
спектром периодической функции.
называется
спектром периодической функции.
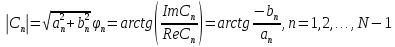
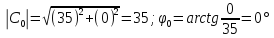

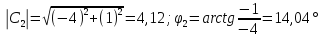
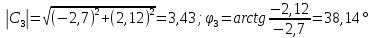

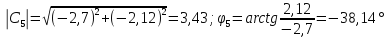
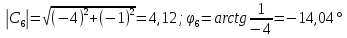

|
|
n = 0 |
n = 1 |
n = 2 |
n = 3 |
n = 4 |
n = 5 |
n = 6 |
n = 7 |
|
|
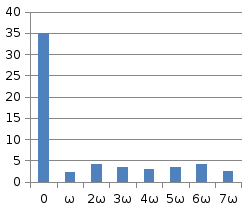
35 |
1,66 |
4,12 |
3,43 |
3 |
3,43 |
4,12 |
2,49 |
|
|
0 |
58,36 |
14,04 |
38,14 |
0 |
-38,14 |
-14,04 |
-58,48 |
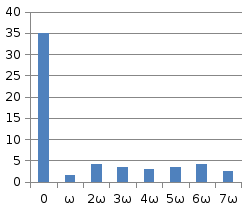
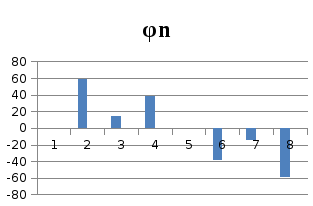
По полученным значениям построим графики амплитудного и фазового спектров:
|
|
|
|
Рисунок 3.2 – Амплитудный спектр сигнала |
Рисунок 3.3 – Фазовый спектр сигнала |
3.4. По полученным значениям ДПФ с помощью ОДПФ восстановить исходные значения отсчетов сигнала.
Обратное ДПФ (ОДПФ) имеет следующий вид:
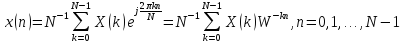
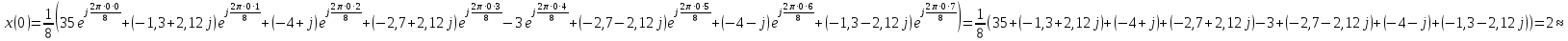 1,
1,
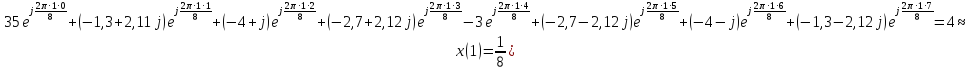 1,
1,
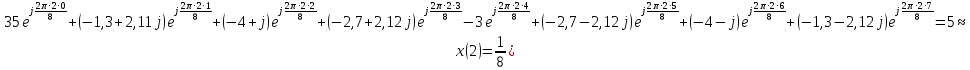 1,4
1,4
 1,41
1,41
 1,41
1,41
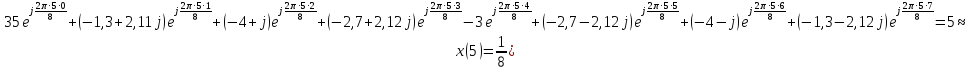 1
1
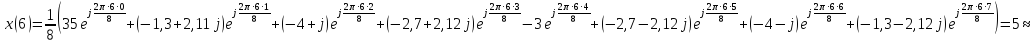 1,4
1,4

4. Лабораторное задание
4.1 Провести вычисления, подтверждающие свойства 1, 2, 5 дискретных экспоненциальных функций.
1.Ортогональность
Функции
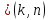 ортогональны, т.е.
ортогональны, т.е.
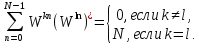
Так
как
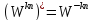 ,
то
,
то

Следствием свойства ортогональности является:
– скалярное
произведение различных двух строк
матрицы
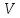 ,
одна из которых должна быть комплексно
сопряженной, равно нулю;
,
одна из которых должна быть комплексно
сопряженной, равно нулю;
– скалярное
произведение одинаковых двух строк
матрицы
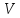 ,
одна из которых должна быть комплексно
сопряженной, равно
,
одна из которых должна быть комплексно
сопряженной, равно
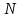 .
.
Рассмотрим в качестве примера матрицу из п.4.1.5:
1.1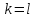
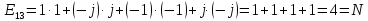
1.2
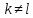
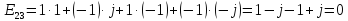
2. Периодичность
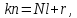 то
то
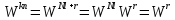 .
.
Построим следующую матрицу и проверим свойство периодичности:

Поскольку
N
= 4, соответственно
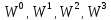 образуют
один период
–
один оборот на комплексной плоскости:
образуют
один период
–
один оборот на комплексной плоскости:
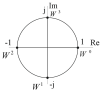
Соответственно проведем следующие вычисления, подтверждающие свойство периодичности:
|
|
|
|
|
|
|
|
|
5. Мультипликативность
Свойство мультипликативности.
– по
строкам
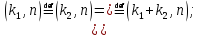
– по
столбцам
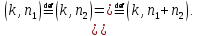
Построим следующую матрицу и проверим свойство мультипликативности:
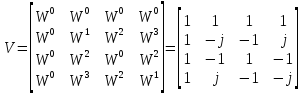
|
|
|
|
|
|
Следовательно, мы убедились в свойстве мультипликативности для строк и столбцов.
4.2
Вычислить спектр дискретизированного
сигнала (п. 3.3), сдвинутого по времени на
 интервалов дискретизации. Построить
графики сигнала, амплитудного и фазового
спектров.
интервалов дискретизации. Построить
графики сигнала, амплитудного и фазового
спектров.
 ,
,
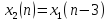
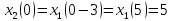
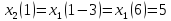
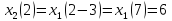

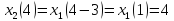
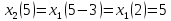
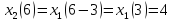
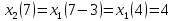
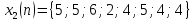 ,
,
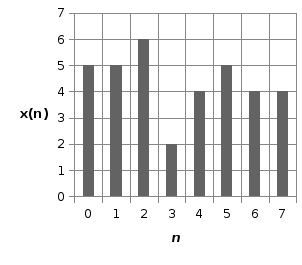
Рисунок 4.1 – График дискретизированного сигнала, сдвинутого на 3Т
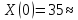
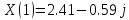

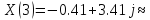
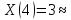
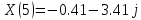

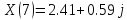

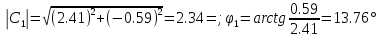
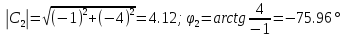
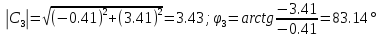
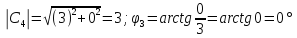

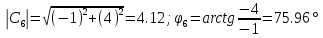
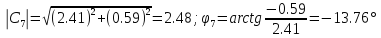
|
|
n = 0 |
n = 1 |
n = 2 |
n = 3 |
n = 4 |
n = 5 |
n = 6 |
n = 7 |
|
|
35 |
2.34 |
4,12 |
3.43 |
3 |
3.43 |
4,12 |
2.48 |
|
|
0 |
13.76 |
-75.96 |
83.14 |
0 |
-83.14 |
75.96 |
-13.76 |
По полученным значениям построим графики амплитудного и фазового спектров:
|
|
|
|
Рисунок 4.2 – Амплитудный спектр сигнала |
Рисунок 4.3 – Фазовый спектр сигнала |
Следовательно, амплитудный спект сигналане зависит от сдвига на t=3T интервалов дискретизации.
4.3 По полученным значениям ДПФ с помощью ОДПФ восстановить значения отсчетов сигнала (п. 4.2). Построить график восстановленного дискретизированного сигнала.
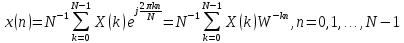
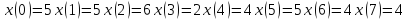
Построим график восстановленного дискретизированного сигнала:
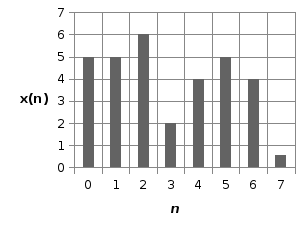
Рисунок 4.1 – Восстановленный дискретизированный сигнал
5. Выводы
В ходе выполнения лабораторной работы мы изучили основные свойства дискретных экспоненциальных функций, а также познакомились с дискретным преобразованием Фурье, обратным дискретным преобразованием Фурье. С помощью ДПФ мы научились переходить от дискретизированного сигнала по времени к дискретизированному сигналу по частоте.

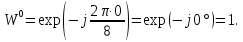
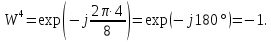
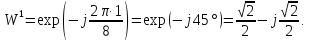
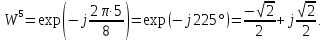
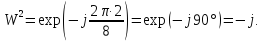
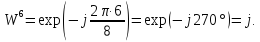

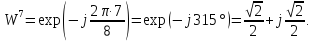

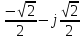
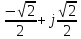
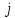

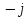
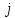
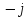
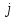
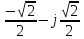
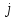
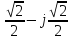
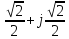

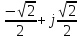
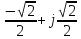
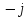
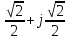
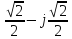
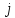
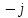
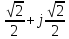

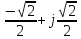
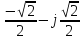

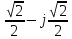
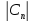
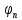 ,
°
,
°
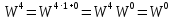
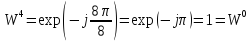
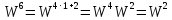
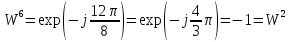
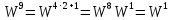
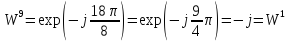
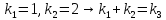
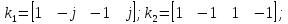
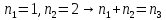
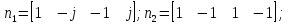
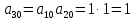
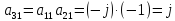
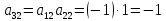
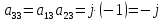
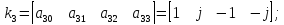
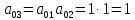
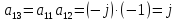

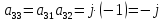


 ,
°
,
°