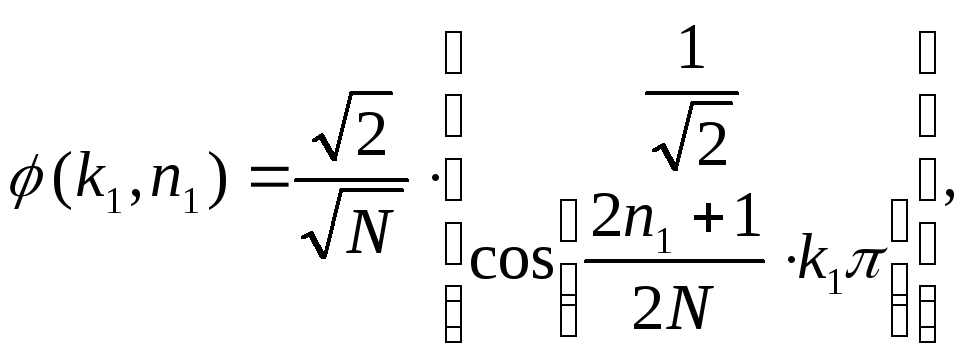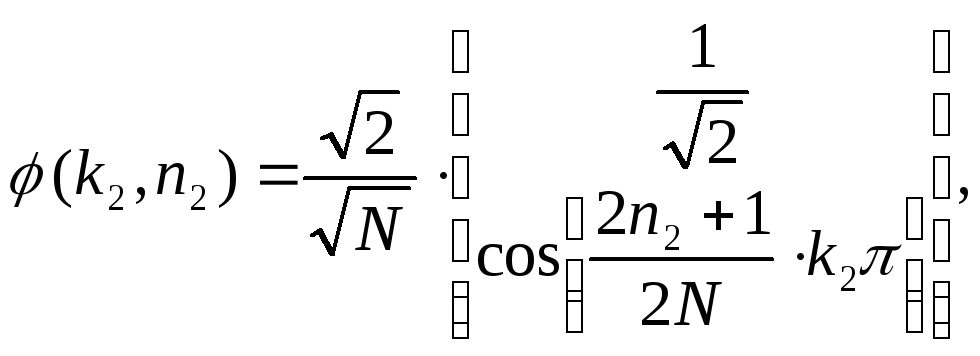- •Дискретное преобразование Уолша-Адамара
- •Дискретное косинусное преобразование
- •Дискретное преобразование Хартли
- •5. Теорема о корреляции. По определению (2.13) корреляционная функция двух конечных последовательностей равна
- •6. Теорема Парсеваля. Пусть последовательности и будут идентичными. В этом случае теорема о корреляции записывается как
Спектр сигнала - результат разложения сигнала на более простые в базисе ортогональных функций.
Квантование — разбиение диапазона значений непрерывной или дискретной величины на конечное число интервалов.
Дискретизация —
преобразование непрерывной функции в
дискретную. (Теорема. 1.
Исходный сигнал может быть полностью
восстановлен при частоте дискретизации
![]() не менее 2W.
2.Сигнал может быть полностью восстановлен
(описан)
не менее 2W.
2.Сигнал может быть полностью восстановлен
(описан)
![]() отсчётами.)
отсчётами.)
Свёртка
фу́нкций —
операция в функциональном
анализе,
показывающая «схожесть» одной функции
с отражённой и сдвинутой копией другой.(
Теорема о свертке. Если исходные
последовательности отсчетов сигналов
![]() и
и ![]() имеют конечные периоды
имеют конечные периоды ![]() ,
их циклическая свертка определяется
формулой:
,
их циклическая свертка определяется
формулой: ![]() ,
𝑛
= 0, 1,…, 𝑁–1.)
,
𝑛
= 0, 1,…, 𝑁–1.)
Корреляционная
функция - это показатель сходства или
общих свойств двух сигналов. Теорема
о корреляции. По определению корреляционная
функция двух
конечных последовательностей ![]() равна:
равна:
![]() ,
для 𝑛
= 0, 1,…,𝑁–1.
,
для 𝑛
= 0, 1,…,𝑁–1.
Периодический
сигнал:![]()
k – любое целое число, Т – период, являющийся конечным отрезком времени.
Дискретным называется сигнал, дискретный во времени и непрерывный по состоянию.
![]() – частота дискретизации
– частота дискретизации
Характеристиками дискретного сигнала явл.(энергия, мощность):
![]()
Взаимная
корреляция ![]() двух сигналов конечного периода
двух сигналов конечного периода ![]() в непрерывной временной области
определяется формулой
в непрерывной временной области
определяется формулой
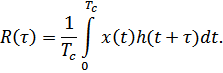
Значение
0 указывает на нулевую корреляцию. Это
означает, что сигналы независимы,
например, если один из сигналов случаен.
Малые значения ![]() указывают на незначительную корреляцию.
указывают на незначительную корреляцию.
Прямое
дискретное преобразование Фурье (ДПФ)
последовательности ![]() определяется как дискретная
последовательности
определяется как дискретная
последовательности ![]() в частотной области (экспоненциальная
форма)
в частотной области (экспоненциальная
форма)
![]() (4.21)
(4.21)
где
![]() – индекс ДПФ
в частотной области,
– индекс ДПФ
в частотной области, ![]() – временной входной последовательности
отсчетов сигнала.
– временной входной последовательности
отсчетов сигнала.
Обратное ДПФ (ОДПФ) имеет следующий вид:
![]() (4.22)
(4.22)
Взаимная
обратимость выражений (4.21) и (4.22)
доказывается подстановкой ![]() в
в ![]() т.е.
т.е.
![]() (4.23)
(4.23)
Так
как ![]() не зависит от
не зависит от ![]() ,
изменяем порядок суммирования в (4.23),
,
изменяем порядок суммирования в (4.23),
![]() (4.24)
(4.24)
В
силу ортогональность ДЭФ внутренняя
сумма отлична от нуля только при ![]() В этом случае, правая часть выражения
(4.24) равна
В этом случае, правая часть выражения
(4.24) равна
![]()
Тригонометрическая форма ДПФ:
-
прямое ДПФ
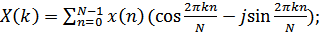
-
обратное ДПФ
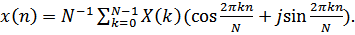
В дискретном преобразовании Фурье используется система комплексных дискретных экспоненциальные функции (ДЭФ), определяемых выражением
![]()
Введем
обозначение ![]() .
Тогда
.
Тогда
![]() .
.
![]() называется поворачивающим множителем.
Переменные
называется поворачивающим множителем.
Переменные ![]() и
и ![]() принимают целочисленные значения
принимают целочисленные значения ![]()
Свойства ДЭФ
1.
Функции ![]() ортогональны, т.е.
ортогональны, т.е.
![]() (4.18)
(4.18)
Так
как ![]() ,
то
,
то
![]()
Следствием свойства ортогональности является:
– скалярное
произведение различных двух строк
матрицы ![]() ,
одна из которых должна быть комплексно
сопряженной, равно нулю;
,
одна из которых должна быть комплексно
сопряженной, равно нулю;
– скалярное
произведение одинаковых двух строк
матрицы ![]() ,
одна из которых должна быть комплексно
сопряженной, равно
,
одна из которых должна быть комплексно
сопряженной, равно ![]() .
.
Действительно,
![]() Сумма
Сумма ![]() единиц даст число
единиц даст число ![]()
Матричная запись свойства ортогональности имеет вид
![]() ,
,
где
![]() –
единичная
матрица.
–
единичная
матрица.
2. Периодичность:
если
![]() то
то ![]() .
(4.19)
.
(4.19)
Поскольку
ДЭФ являются периодическими функциями,
матрицу (4.16) можно переписать с минимальными
фазами ![]() ,
образующимися после вычитания из
значения
,
образующимися после вычитания из
значения ![]() целого числа периодов
целого числа периодов ![]() т.е.
т.е.
![]() .
.
Для
![]() матрицу ДЭФ (4.16) с минимальными фазами
матрицу ДЭФ (4.16) с минимальными фазами
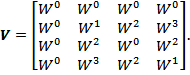
3. Симметричность.
ДЭФ
является функцией двух переменных ![]() Выводы относительно одной из переменных
справедливы и для другой. Тогда
Выводы относительно одной из переменных
справедливы и для другой. Тогда
![]()
4. Обратная матрица ДЭФ.
Из
свойства ортогональности ![]() .
Умножим обе части этого равенства слева
на
.
Умножим обе части этого равенства слева
на ![]()
![]()
![]() .
(4.20)
.
(4.20)
5. Мультипликативность:
– по
строкам ![]()
– по
столбцам ![]()
Действительно,
![]() .
При умножении любых двух строк (столбцов)
матрицы
.
При умножении любых двух строк (столбцов)
матрицы ![]() получается
строка (столбец) той же матрицы. Номер
полученной строки (столбца) равен сумме
номеров сомножителей.
получается
строка (столбец) той же матрицы. Номер
полученной строки (столбца) равен сумме
номеров сомножителей.
Дискретное преобразование Уолша-Адамара
Пусть
сигнал ![]() представлен
совокупностью своих равноотстоящих
отсчетов),
представлен
совокупностью своих равноотстоящих
отсчетов),![]() .
Выражения
.
Выражения
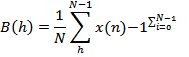
|
B(h)= |
(13)
|
|
S(x)= |
(14)
|
образуют пару дискретных преобразований Уолша-Адамара в показательной форме, формула (13) называется прямым преобразованием Уолша-Адамара (ДПУА) и дает спектр сигнала в базисе Уолша, формула (14) называется обратным преобразованием Уолша-Адамара. [6]
Матрицей Адамара называется ортогональная квадратная матрица, элементами которой являются действительные числа 1 и -1. Простейшей матрицей Адамара является матрица порядка два:
![]() .
.
Используя матрицу Адамара, запишем преобразования (15) и (16) в матричной форме:
|
B
=
|
(15) |
|
S
=
|
(16) |
где B = [B(0), B(1), …,B(N-1)] – вектор коэффициентов преобразования Уолша-Адамара;
S = [S(0), S(1), …,S(N-1)] – вектор отсчетов входного сигнала;H - матрица Адамара порядка N. [6]
Вычисление
по формулам (13), (14) требует N(N-1)
операций. Существуют быстрые алгоритмы
(быстрые преобразования Адамара (БПУА)),
которые требуют только N
log![]() N
операций. Их сущность заключается в
разбиении матрицы Адамара в произведение
слабозаполненных матриц. Процесс
умножения на матрицу Адамара заключается
в последовательном умножении на
слабозаполненные матрицы. Вывод:
Вычислительные преимущества БПУА по
сравнению ДПУА следующие: ДПУА требует
N(N-1)
операций, а БПУА требуют только N
log
N
операций. Их сущность заключается в
разбиении матрицы Адамара в произведение
слабозаполненных матриц. Процесс
умножения на матрицу Адамара заключается
в последовательном умножении на
слабозаполненные матрицы. Вывод:
Вычислительные преимущества БПУА по
сравнению ДПУА следующие: ДПУА требует
N(N-1)
операций, а БПУА требуют только N
log![]() N
операций. Таким образом, вычислительная
экономия составляет N(N-1)
/ N
log
N
операций. Таким образом, вычислительная
экономия составляет N(N-1)
/ N
log![]() N.
Например, если N=1024,
то выигрыш составит 1024(1024-1)/1024 log
N.
Например, если N=1024,
то выигрыш составит 1024(1024-1)/1024 log![]() 1024=102,3
раза.
1024=102,3
раза.
Дискретное косинусное преобразование
Дискретное косинусное преобразование непосредственно связано с ДПФ. Недостаток ДПФ заключается в том, что спектральные коэффициенты носят комплексный характер. Однако можно осуществить такое преобразование множества отсчетов сигнала Х(n), в котором используется только реальная часть ядра преобразования ДПФ, т.е. только члены, связанные с соs. Используя запись ДПФ, получаем выражения для прямого (17) и обратного (18) ДКП:
|
C(k)
=
|
(17)
|
|
X |
(18) |
где
с(k)
=
![]() для k
для k![]() 0,
0,
1
для k![]()
![]()
Матричная форма записи ДКП имеет вид:
Прямое одномерное ДКП
|
|
(19)
|
где
[С(k)]
– вектор- столбец спектральных
коэффициентов ДКП размером (N![]() 1);
1);
|
|
(20) |
где
[![]() ]
матрица дискретного множества функций
ДКП размером (N
]
матрица дискретного множества функций
ДКП размером (N![]() N);
N);
[X(n)]
– вектор-столбец отсчетов сигнала
размером (N![]() 1).
[6]
1).
[6]
Обратное одномерное ДКП
|
|
(21) |
Прямое
ДКП двухмерного фрагмента изображения
размером (N![]() N)
запишется как
N)
запишется как
|
|
(22)
|
где
[C(![]() )]
– матрица спектральных коэффициентов
ДКП размером (N
)]
– матрица спектральных коэффициентов
ДКП размером (N![]() N);
N);
[X(n![]() )]
– сигнальная матрица размером (N
)]
– сигнальная матрица размером (N![]() N);
N);
[![]() ]
– матрица ДКП размером (N
]
– матрица ДКП размером (N![]() N)
в соответствии с формулой (19):
N)
в соответствии с формулой (19):
|
|
23)
|
где
![]() - матрица ДКП размером (N
- матрица ДКП размером (N![]() N):
N):
|
|
(24)
|
Прямое двухмерное преобразование ДКП в матричной форме имеет вид:
|
[C( |
(25)
|
Обратное преобразование в матричной форме записывается как
|
|
(26) |

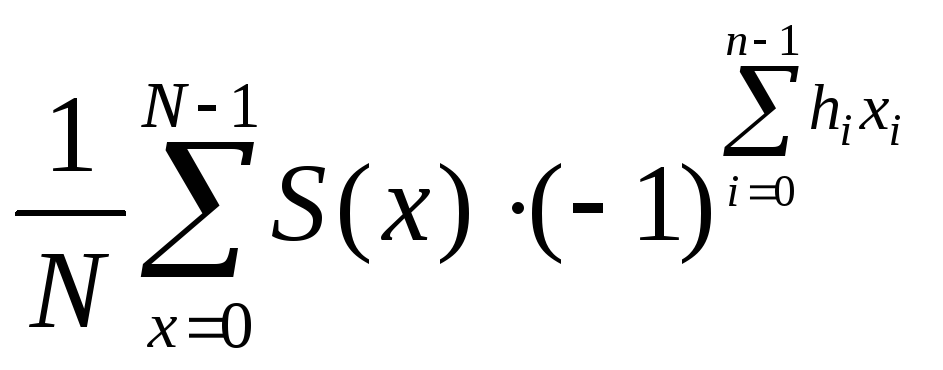 ,
h=0,1,2,…,N-1,
,
h=0,1,2,…,N-1,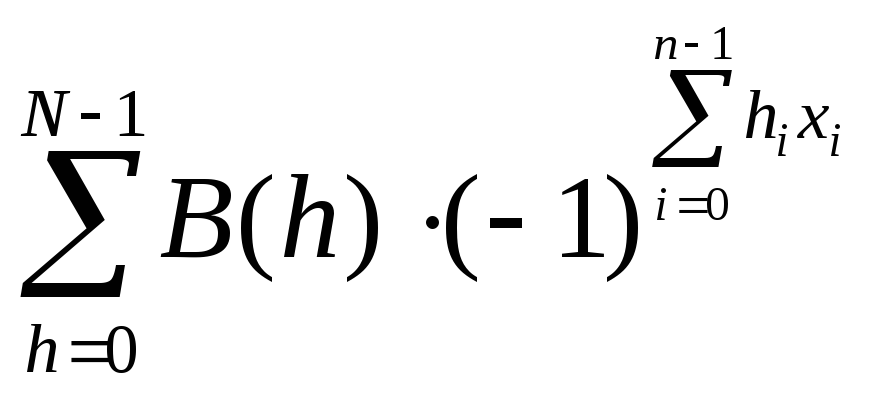 ,
h=0,1,2,…,N-1,
,
h=0,1,2,…,N-1,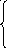 (n)
=
(n)
=