2.3. Передаточная функция и временные характеристики звеньев

Основной характеристикой звена САУ является его дифференциальное уравнение. Однаконаряду с ним в теории управления нашли применение и другие характеристики. Важнейшей из них является передаточная функция, получаемая на основе применения преобразования Лапласа к исходному дифференциальному уравнению звена. Прямое и обратное преобразования Лапласа определяются следующими выражениями: ;, гдеy(t) – оригинал; Y(s) – изображение функции y(t); s – комплексная переменная; и – символы прямого и обратного преобразования Лапласа.

Наиболее важные свойства преобразования Лапласа, а также соответствие между рядом оригиналов и изображений приведены в приложении.

Если в дифференциальном уравнении звена (2.1) положить , то после применения прямого преобразования Лапласа получим алгебраическое уравнение относительно изображений:, откуда

. (2.7)

Пepeдаточная функция звена W(s) есть отношение изображения выходного сигнала к изображению входного сигнала при нулевых начальных условиях.

Если взять дифференциальное уравнение звена в операторной форме (2.3), то формально W(s) получим делением оператора B(p) на оператор A(p) с заменой p на s: .

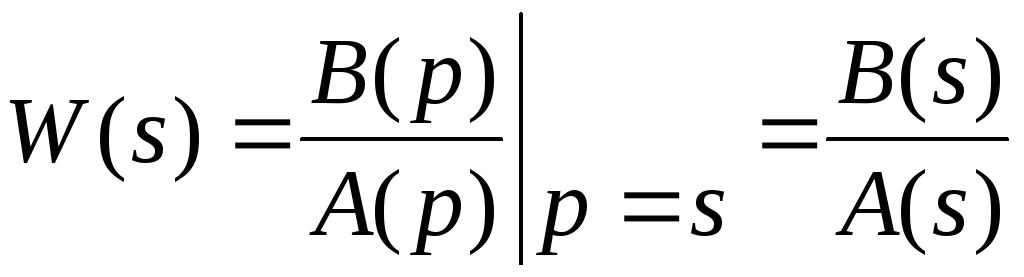Из (2.7) следует связь изображений входа и выхода через передаточную функцию:

. (2.8)

Звено САУ на структурных схемах изображают так, как показано на рис. 2.3.

Рис. 2.3

При использовании уравнения (2.2) передаточную функцию звена будем записывать в виде

, (2.9)

где N(s) и L(s) – многочлены с единичными коэффициентами в младших членах.

Полином L(s) будем называть xapактepистичecким полиномом, а уравнение –характеристическим уравнением звена.

Следующий класс характеристик звена – это временные характеристики: весовая и переходная функции звена.

Если рассматривать W(s) как изображение, то приходим к понятию весовой (импульсной) функции звeнa w(t), формально определяемой как обратное преобразование Лапласа от передаточной функции

. (2.10)

Вeсовая функция звена w(t) ecть реакция звена на входной сигнал в виде дельта-функции, которая определяется соотношением

, причем

Дельта-функция обладает фильтрующим свойством: .

Если положить , тои, откуда, т.е. – реакция звена на входной сигнал .

К такому же результату можно прийти следующим образом. Правой части (2.8) соответствует в области оригиналов свертка функций и:

. (2.11)

Если в (2.11) положить , то на основании фильтрующего свойства дельта-функции будем иметь .

Пepexодной функциeй звена называется реакция звена на единичное ступенчатое воздействие

Так как , то и по определению

. (2.12)

Так как , тo , а.

Пример 2.3. Дифференциальное уравнение двигателя постоянного тока (пример 2.1) по углу поворота в предположении, что , можно записать в виде , где принято .

Передаточная функция и временные характеристики будут иметь вид

, ,

.

2.4. Частотные характеристики звеньев

Частотные характеристики определяют динамические свойства звеньев при воздействии на них гармонических сигналов. формально частотные характеристики получаются из передаточной функции W(s) при , где – угловая частота, имеющая размерность [рад/с]. Сделав такую замену, получим

(2.13)

т.е. частотная передаточная функция есть прямое преобразование Фурье от весовой функцииw(t).

Комплекснозначную функцию частотыбудем называтьамплитудно-фазовой частотной xаpактepистикой (АФЧХ) звена.

Как любое комплексное число АФЧХ можно представить в виде

, (2.14)

где

, (2.15)

. (2.16)

Если передаточная функция звена представлена в виде , то. При этом, очевидно, (считаем) и.

В соответствии с (2.14)–(2.16) имеем еще ряд частотных характеристик: – амплитудно-частотная xаpактepистика (АЧХ); –фазово-частотная xаpактepистика (ФЧХ); , – соответственно вeществeнная и мнимая частотные характеристики.

Рассмотрим физический смысл частотных характеристик. Если на вход звена с передаточной функцией W(s) поступает гармонический сигнал , то в установившемся режиме после затухания переходной составляющей выходной сигналбудет также гармоническим:, т.е. той же частоты, но измененных амплитуды и фазы.

Изменение амплитуды определяется модулем , а фазы – аргументомна соответствующей частоте.

На практике для наглядности частотные характеристики изображают в виде графиков при изменении частоты от 0 до.

Частотные характеристики обладают следующими свойствами: ,,,, которые непосредственно следуют из (2.14)–(2.16). Другими словами: характеристики,являются четными,,– нечетными. В силу этого графики при изменении частотыoт –∞ до 0 не строятся. АФЧХ представляет собой годограф на комплексной плоскости с координатамиu, v или А, при изменении от 0 до.

На рис. 2.4 и 2.5 представлены иллюстративные графики частотных характеристик некоторого звена.

Рис. 2.4

Штриховой линией показаны части графиков, соответствующие . Вполне понятно, что из графика (см. рис. 2.4) нетрудно получить графики а, б или соответственно в, г (см. рис. 2.5) и наоборот.

Рис. 2.5

На практике часто применяются соответствующие логарифмические частотные характеристики: логаpифмичeская амплитудная частотная характеристика (ЛАЧХ) илогарифмическая фазовая частотная xаpактepистика (ЛФЧХ) , графики которых строятся в логарифмическом масштабе. При построениипо оси ординат откладывается величина, единицей измерения которой является децибел, а по оси абсцисс – частота[1/с] в логарифмическом масштабе, т.е. величина. Увеличениев 10 раз соответствует приращениювдоль оси ординат на 20 дБ. При построении ЛФЧХ величинуоткладывают по оси ординат в обычном масштабе (в градусах или радианах),a – в логарифмическом масштабе.

На рис. 2.6 приведены иллюстративные графики ЛАЧХ и ЛФЧХ для некоторого звена. Частота , при которой, носит название частоты среза. Левее значения (усиление), правее –(ослабление амплитуды гармонического сигнала).

Рис. 2.6