8.2. Схемы моделирования и виды уравнений состояния

В зависимости от структуры матрицы А в (8.3) из общего класса уравнений состояния выделяют два подкласса. Если матрица А в (8.3) является диагональной:

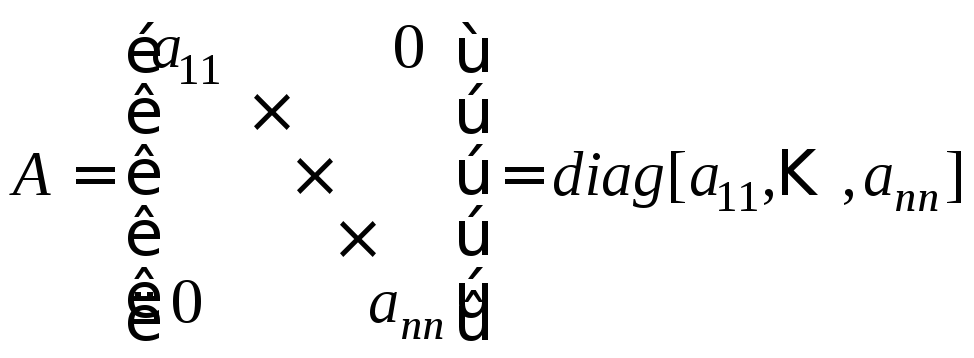(8.5)

или в общем случае представлена в форме Жордана, то имеем каноническую форму уравнений состояния. Примером матрицы в форме Жордана может служить матрица

размерностью 4×4, имеющая одну клетку Жордана размерностью 3×3.

Если матрица А в (8.3) представлена в виде

, (8.6)

то уравнения состояния имеют нормальную форму. Матрицу такой структуры называют сопровождающей матрицей или матрицей Фробениуса.

Пусть в уравнении (8.3) матрица , т.е.,и матрицаА является матрицей Фробениуса (8.6). Тогда, очевидно, ,,…,, т.е. в качестве переменных состояния выбрана сама выходная координатаy и ее производные. В этом частном случае вектор состояния называют фазовым вектором, а пространство состояния – фазовым пространством.

Для более ясного понимания внутренней структуры и взаимосвязи отдельных переменных системы, описываемой уравнениями состояния, применяют графическую интерпретацию уравнений состояния в виде структурных схем, которые иногда называют схемами моделирования. При этом используются три основных блока, показанные на рис. 8.1: а) сумматор , б) интегратор, в) блок преобразования (усиления), гдеА – некоторая матрица.

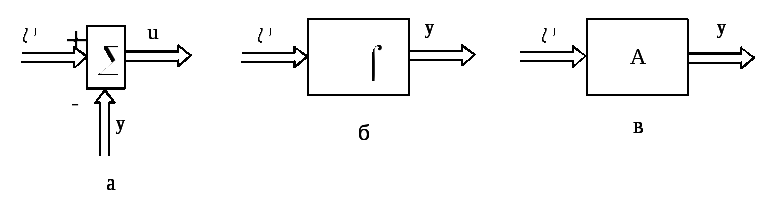
Рис. 8.1

Используя указанные блоки, можно изобразить схему моделирования по уравнениям (8.2), представленную на рис. 8.2.

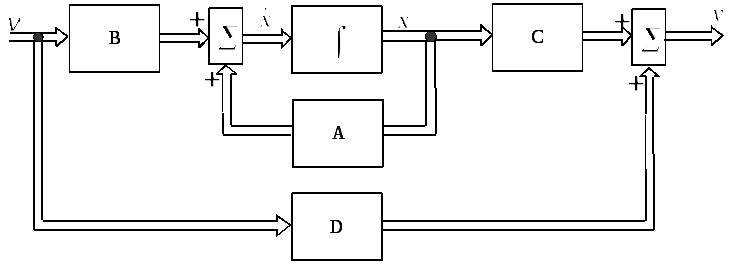
Рис. 8.2

Пример 8.2. Рассмотрим САУ из примера 8.1. В соответствии с полученными уравнениями состояния (8.4) нетрудно изобразить схему моделирования, представленную на рис. 8.3.

Рис. 8.3

Для этого же примера получим другую структуру схемы моделирования и соответственно другую форму уравнений состояния. Выходной сигнал y и сигнал ошибки e можно связать следующим уравнением в области изображений: , откуда нетрудно получить дифференциальное уравнение разомкнутой системы. С учетом уравнения замыканияполучим дифференциальное уравнение замкнутой системы, в соответствии с которым нетрудно получить схему моделирования (рис. 8.4).

Если обозначить выходы интеграторов через и, как показано на рис. 8.4, то можно в соответствии со схемой моделирования записать следующие уравнения:,,.

υ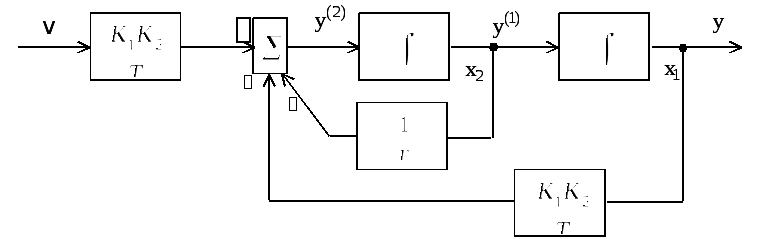

Рис. 8.4

Вводя вектор состояния , уравнения представим в виде

, . (8.7)

Уравнения (8.4) и (8.7) имеют различный вид, как и схемы моделирования (см. рис. 8.3 и 8.4), но описывают одну и ту же систему. Уравнения состояния (8.7) имеют нормальную форму, они составлены относительно фазовых координат.

8.3. Преобразование уравнений состояния

Пусть система описывается уравнениями состояния общего вида (8.3). Сделаем в этих уравнениях замену переменных x = Qz, где – новый вектор состояния,Q – произвольная матрица размерностью с постоянными коэффициентами. На матрицу Q накладывается единственное ограничение – она должна быть невырожденной (неособенной), т.е. определитель этой матрицы . В этом случае всегда существует обратная матрица, которую будем обозначать через, такая, что, где– единичная матрица размерностью. Очевидно, что при этих условиях существует однозначная связь между векторамиx и z: ,.

В уравнениях (8.3) сделаем замену x = Qz и с учетом того, что , получим

, . (8.8)

Уравнения (8.8) будут новыми уравнениями состояния, имеющими основную матрицу системы , входаи выходаCQ. Так как Q – произвольная матрица, то исходным уравнениям (8.3) соответствует бесчисленное количество эквивалентных уравнений состояния (8.8).

Отметим, что две матрицы A и , связанные преобразованием, называются подобными. Подобные матрицы имеют одинаковые собственные значения.

Используя линейное преобразование, можно поставить задачу о выборе при исследовании той или иной формы уравнений состояния. Наиболее часто решается задача преобразования исходной системы (8.3) к нормальной или канонической форме уравнений состояния (8.8).

Доказано, что для произвольной матрицы А всегда существует невырожденная квадратная матрица размерностью , которую обозначим черезM и назовем модальной, такая, что матрица будет иметь форму Жордана. Если матрицаА имеет различные собственные значения (числа) , являющиеся корнями характеристического уравнения

, (8.9)

то матрица будет диагональной:.

Таким образом, преобразование произвольной системы уравнений (8.3) к канонической форме всегда возможно. Наиболее просто задача определения модальной матрицы решается для случая различных собственных чисел матрицы А, которые обозначим через . Для каждого собственного числанаходится собственный векториз решения векторно-матричного уравнения

. (8.10)

Матрица, образованная вектор-столбцами , т.е. матрица

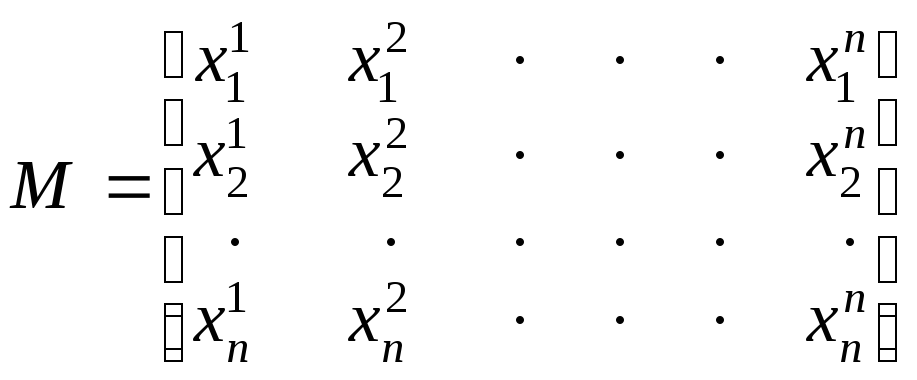, (8.11)

и будет искомой модальной матрицей.

В соответствии с (8.9) при определитель системы линейных уравнений (8.10) равен нулю, т.е. система имеет бесчисленное множество решений, каждое из которых можно принять за собственный вектор. Отсюда матрицаМ является неединственной.

В случае кратных собственных значений матрицы А задача определения модальной матрица значительно усложняется.

В частности, если исходная матрица А является матрицей Фробениуса вида

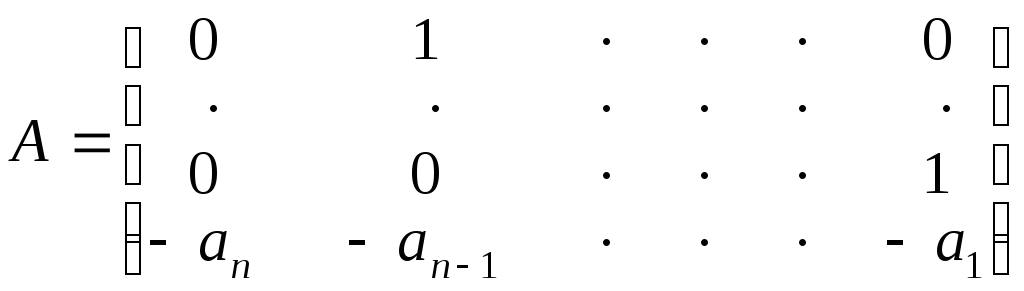(8.12)

и собственные числа , являющиеся корнями характеристического уравнения

= 0, (8.13)

различны, то модальная матрица будет иметь вид

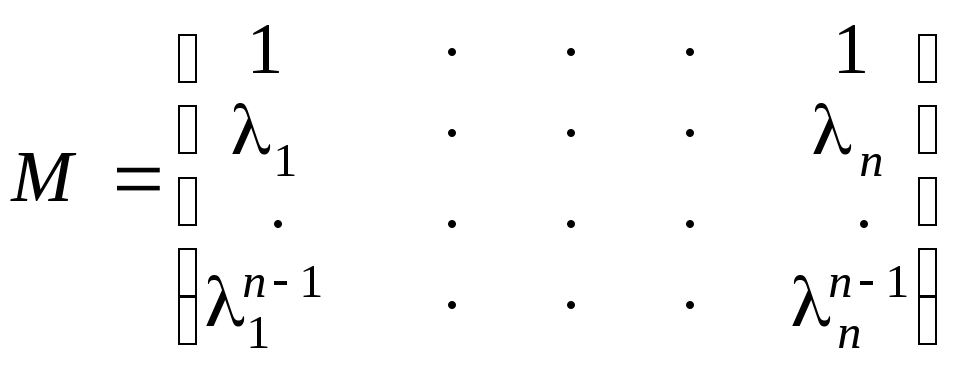. (8.14)

Пример 8.3. Пусть в САУ, которая рассматривалась в примерах 8.1 и 8.2,  с, , тогда уравнения (8.7) будут иметь вид

, . (8.15)

Преобразуем уравнения состояния к канонической форме. Основная матрица системы А является матрицей Фробениуса. Найдем ее собственные значения из решения характеристического уравнения

.

Корни уравнения будут различными: ,. Таким образом, в соответствии с (8.14) определяем модальную матрицу M и обратную ей :

, .

Далее M^–1AM = diag[–2+ j4, –2 – j4], , .

Итак, уравнения состояния (8.15) преобразуются к канонической форме:

, .

Пример 8.4. Пусть система описывается уравнениями состояния

, .

Корни характеристического уравнения будут ,.

Находим собственные векторы из решения системы линейных уравнений ,.

Полагая , будем иметь

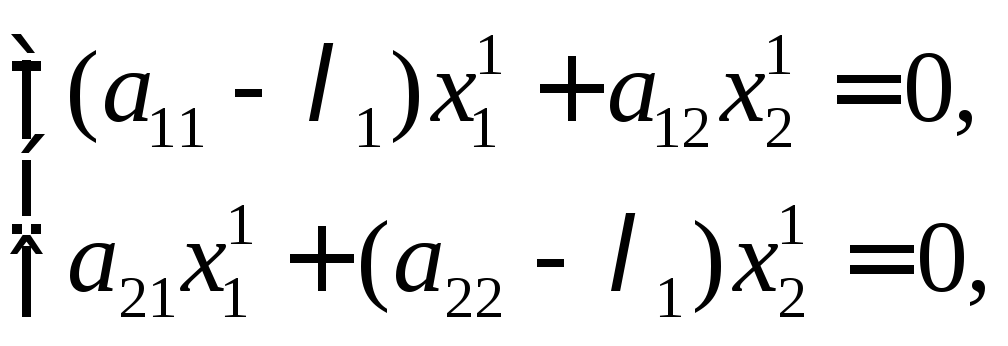
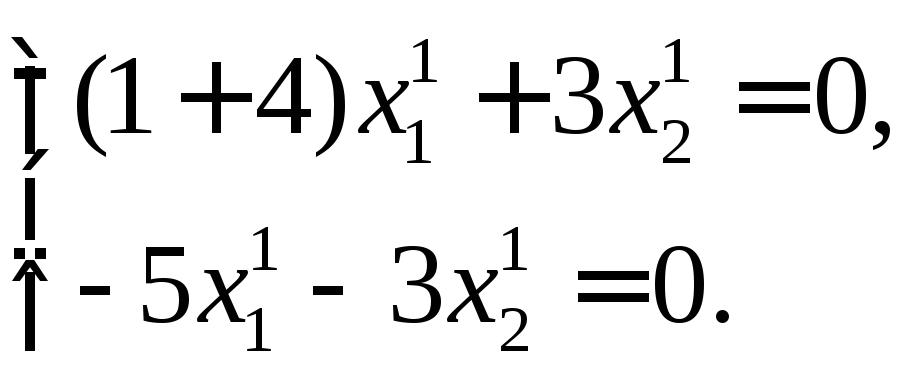
Из последних двух уравнений , откуда, задавая, например, , получим . Итак, первый собственный вектор . При в конечном итоге для определения координат второго собственного вектора получим . Полагая , будем иметь и соответственно . Итак, матрицу М можно выбрать в виде

, .

, ,.

Окончательно уравнения в канонической форме будут иметь следующий вид:

, .