8.4. Нормальная форма уравнений состояния одномерной системы

Пусть динамика одномерной системы, имеющей один вход и один выход, описывается дифференциальным уравнением

, (8.16)

где ,.

Требуется найти уравнения состояния (8.3) в нормальной форме, эквивалентные уравнению (8.16).

Задача легко решается для частного случая (8.16), если m = 0, т.е. правая часть (8.16) будет иметь вид .в (8.16) сделаем замену переменных . Дифференцируя последовательно каждое равенство, получим

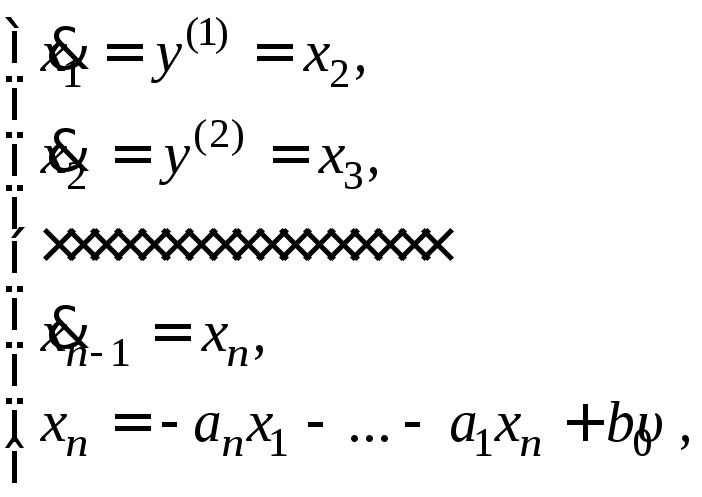
где последнее соотношение соответствует уравнению (8.16). Полученную систему с учетом запишем в виде уравнений состояния в нормальной форме:

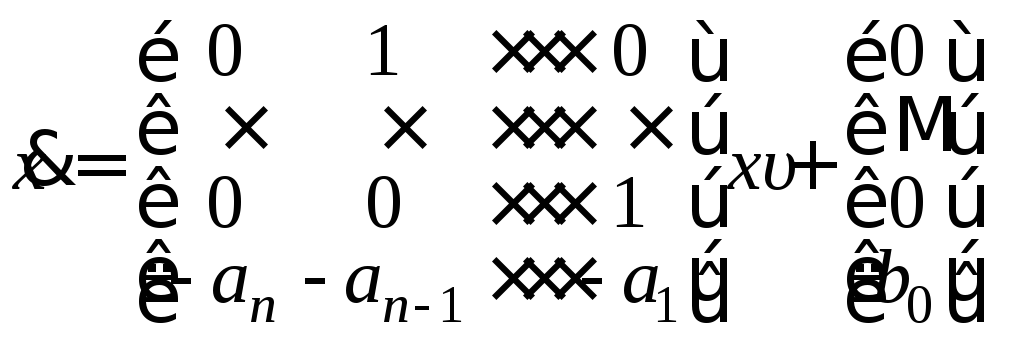, , (8.17)

где, как обычно, .

Если в (8.16) m > 0, то также можно получить уравнения состояния в нормальной форме. Вывести их несколько сложнее, поэтому дадим конечный результат. Для удобства будем в (8.16) полагать m = n. Очевидно, если m < n, то ряд первых коэффициентов будет равен нулю. Уравнения состояния в этом случае будут иметь следующий вид:

, . (8.18)

Коэффициенты определяются из решения системы линейных алгебраических уравнений, записанных в векторно-матричной форме:

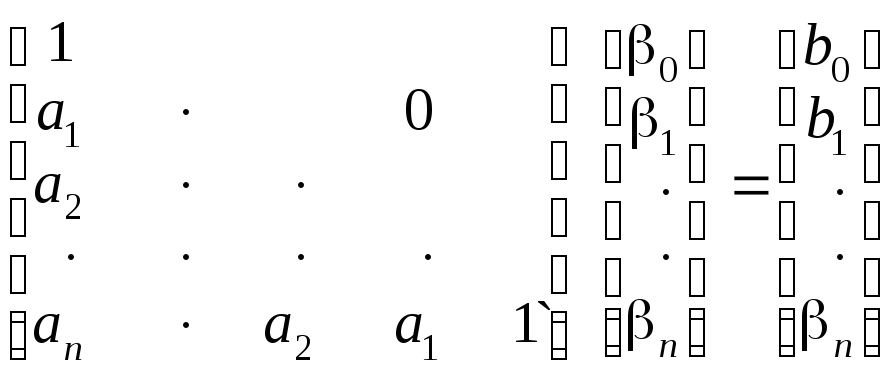. (8.19)

Из (8.19) следует, что ,,,…, откуда последовательно находятся,,… .

Для физически реализуемых систем и.

Пример 8.5. Рассмотрим замкнутую систему управления стандартной структуры (см. рис. 3.1), где будем полагать ,,,,с,с,с.

Передаточная функция разомкнутой системы будет равна

.

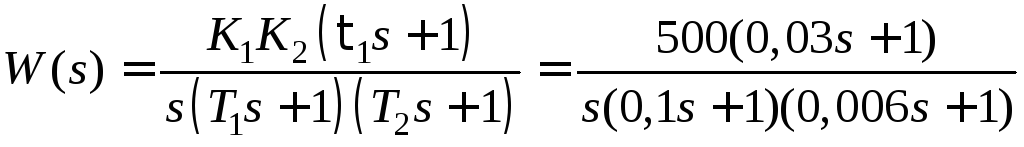Найдем дифференциальное уравнение разомкнутой системы, связывающее y и e: .

Коэффициенты этого уравнения ,,,,,,.

Уравнение для определения имеет вид

,

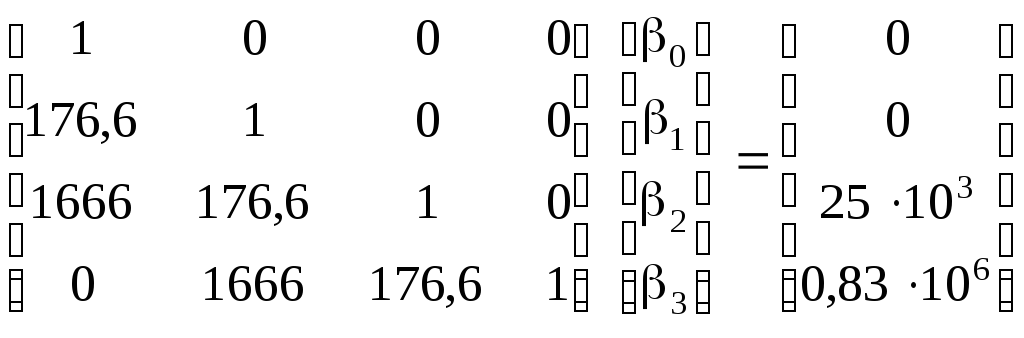откуда ,,,.

Итак, уравнения состояния разомкнутой системы в нормальной форме имеют вид

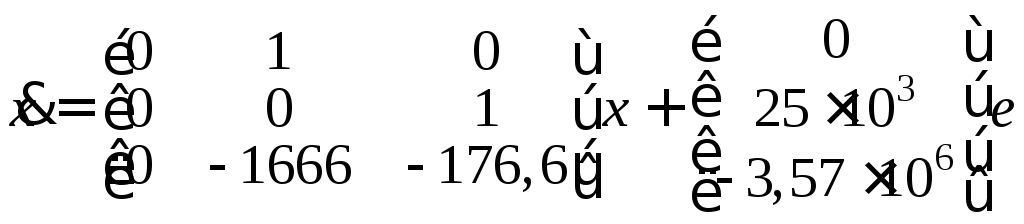, . (8.20)

Для получения уравнений состояния замкнутой системы учтем уравнение замыкания , после подстановки которого в (8.20) получим

, . (8.21)

Уравнения состояния замкнутой системы (8.21) уже не являются уравнениями в нормальной форме.

8.5. Каноническая форма уравнений состояния одномерной системы

Для получения уравнений состояния одномерной системы в канонической форме используется передаточная функция системы. Будем полагать, что система описывается дифференциальным уравнением (8.16), которому соответствует передаточная функция .

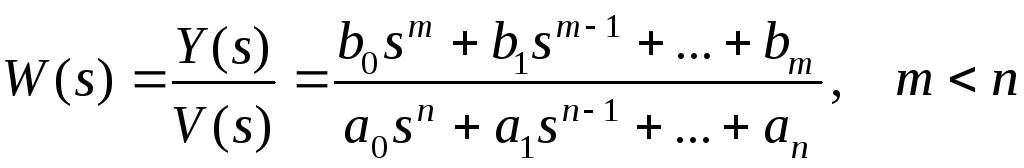Пусть характеристическое уравнение системы имеет n различных корней , тогда передаточную функцию можно представить в виде

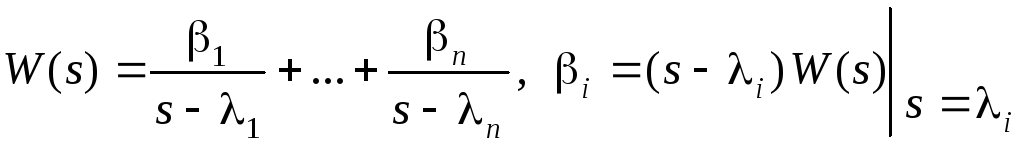. (8.22)

Очевидно, что в этом случае .

Обозначим , тогда,.

Перейдем в операторных соотношениях к оригиналам, полагая . Получим,,.

Вводя вектор состояния , запишем полученные уравнения в виде уравнений состояния

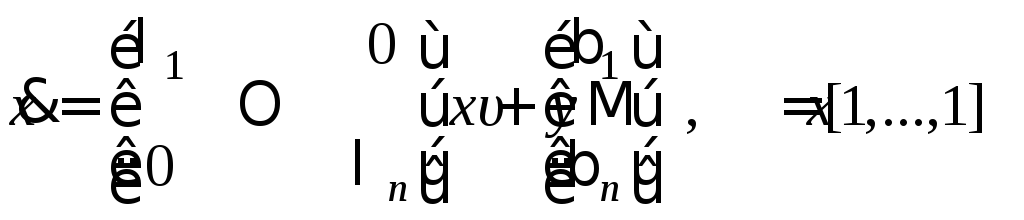. (8.23)

Итак, получили уравнения состояния в канонической форме с диагональной матрицей коэффициентов, где в общем случае элементы ,матриц могут быть и комплексными величинами.

Из (8.22) можно получить другую каноническую форму уравнений состояния. Если обозначить , то проводя аналогичные рассуждения, получим уравнения состояния:

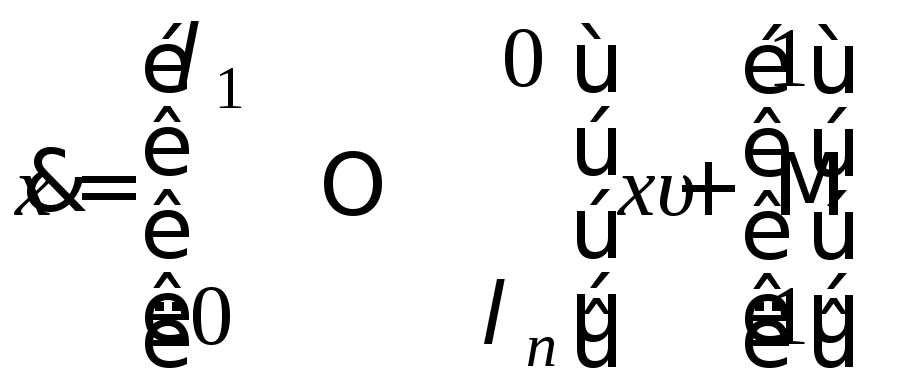, . (8.24)

Рассмотрим теперь случай кратных корней. Пусть характеристическое уравнение имеет корни кратностиk, а остальные корни простые.

Тогда передаточную функцию можно представить в виде разложения

,

где ,

.

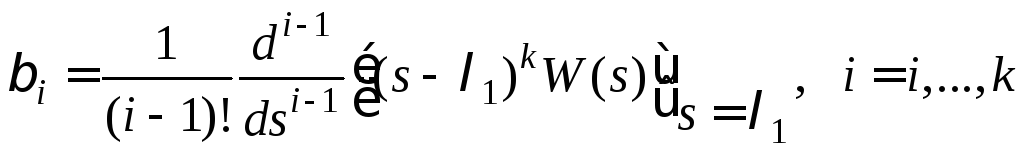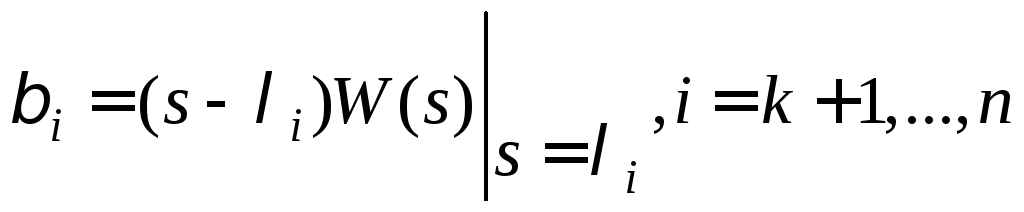в этом случае 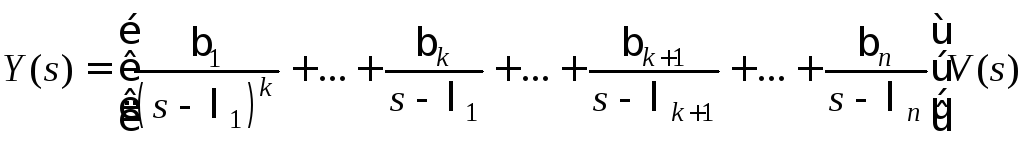или .

Между изображениями существует связь. Полагаяи переходя к оригиналам, получим в области оригиналов:;;;.

Вводя вектор состояния , полученные соотношения запишем в векторно-матричной форме:

(8.25)

Уравнения состояния (8.25) имеют каноническую форму, основная матрица – форму Жордана. Корню кратности k соответствует клетка Жордана размерностью . Очевидно, при наличии нескольких кратных корней будем получать соответствующие клетки Жордана для каждого корня.

Пример 8.6. Обратимся к системе управления из примера 8.5 и найдем уравнения состояния в канонической форме для разомкнутой системы. Характеристическое уравнение разомкнутой системы имеет три различных корня:,,. Используя выражение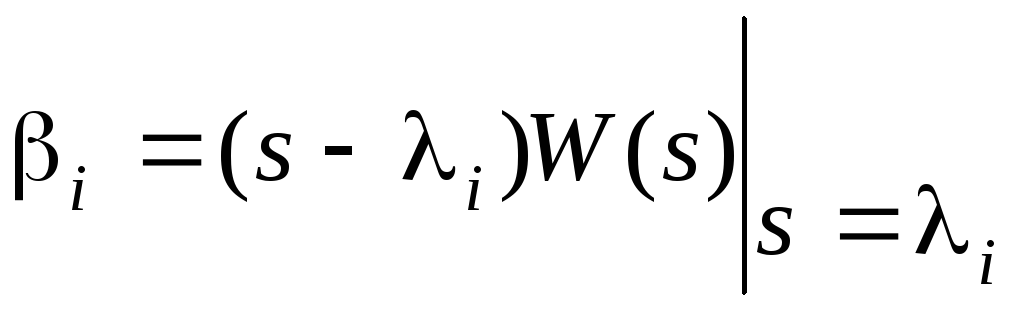, находим величины :,,. Таким образом, уравнения состояния в канонической форме для разомкнутой системы имеют вид

, .

С учетом уравнения замыкания нетрудно получить следующие уравнения состояния замкнутой системы:

, (8.26)

Сравнивая (8.21) и (8.26), видим, что одна и та же система описывается разными уравнениями состояния, которые эквивалентны между собой.