
- •Теория автоматического управления
- •В. П. Кузнецов, с. В. Лукьянец, м. А. Крупская
- •Часть 1
- •I-53 01 07 «Информационные технологии и управление
- •Введение
- •1. Общие сведения о системах автоматического управления
- •1.1. Основные понятия и определения
- •1.2. Классификация систем автоматического управления
- •1.3. Примеры систем автоматического управления
- •2. Математическое описание звеньев систем автоматического управления
- •2.1. Уравнения звеньев
- •2.2. Линеаризация уравнений динамики звеньев
- •2.3. Передаточная функция и временные характеристики звеньев
- •2.4. Частотные характеристики звеньев
- •2.5. Элементарные звенья и их характеристики
- •2.6. Особенности и физическая реализуемость звеньев
- •3. Математическое описание систем автоматического управления
- •3.1. Структурные схемы и структурные преобразования
- •3.2. Передаточные функции и уравнения систем
- •3.3. Частотные характеристики систем
- •4. Процессы в системах автоматического управления
- •4.1. Общее описание процессов
- •4.2. Аналитические методы вычисления процессов
- •4.3. Моделирование переходных процессов на пэвм
- •5. Устойчивость процессов в системах автоматического управления
- •5.1. Понятие устойчивости линейных систем
- •5.2. Алгебраические критерии устойчивости
- •5.3. Критерий устойчивости Михайлова
- •5.4. Критерий устойчивости Найквиста
- •5.5. Построение областей устойчивости
- •6. Точность систем автоматического управления
- •6.1. Понятие точности. Постоянные ошибки
- •6.2. Установившиеся ошибки при произвольном входном сигнале
- •6.3. Установившиеся ошибки при гармоническом воздействии
- •7. Оценки качества переходных процессов
- •7.1. Корневые оценки качества
- •7.2. Интегральные оценки качества
- •7.3. Частотные оценки качества
- •8. Уравнения состояния линейных систем
- •8.1. Описание систем управления с помощью уравнений состояния
- •8.2. Схемы моделирования и виды уравнений состояния
- •8.3. Преобразование уравнений состояния
- •8.4. Нормальная форма уравнений состояния одномерной системы
- •8.5. Каноническая форма уравнений состояния одномерной системы
- •8.6. Переходная матрица состояния
- •8.7. Передаточная и весовая матрицы
- •8.8. Устойчивость, управляемость и наблюдаемость линейных систем
- •9. Синтез систем автоматического управления
- •9.1. Предварительные замечания
- •9.2. Корректирующие устройства
- •9.3. Корректирующие устройства по внешнему воздействию
- •9.4. Синтез сау на основе логарифмических частотных характеристик
- •9.5. Модальный метод синтеза (метод размещения полюсов)
- •Приложение
- •Литература
- •Теория автоматического управления
- •Часть 1
9.4. Синтез сау на основе логарифмических частотных характеристик
Общий порядок синтеза системы включает следующие этапы:
1. По
виду передаточной функции исходной
системы
![]() строится ЛАХ исходной системы
строится ЛАХ исходной системы![]() .
При этом исходная система должна иметь
функционально необходимые элементы и
должна быть минимально-фазовой.
.
При этом исходная система должна иметь
функционально необходимые элементы и
должна быть минимально-фазовой.
2. На
основании требований к САУ строится
желаемая ЛАХ
![]() .
.
3. Путем
сравнения характеристик
![]() и
и![]() определяется
определяется![]()
![]() (если коррекция последовательная). Эту
коррекцию также можно пересчитать к
параллельной или встречно-параллельной.
(если коррекция последовательная). Эту
коррекцию также можно пересчитать к
параллельной или встречно-параллельной.
4. По
виду
![]() определяется структурная схема и
параметры
коррекции.
определяется структурная схема и
параметры
коррекции.
5. Производится моделирование системы на ЦВМ (например в среде Matlab), уточняются параметры САУ.
6. Производится реализация коррекции с помощью регуляторов или программно.
Построение ЛАХ исходной системы не вызывает затруднений. Рассмотрим подробнее построение желаемой ЛАХ.
Учет требований точности САУ:
а)
пусть
даны рабочая частота
![]() и амплитуда
и амплитуда
![]() задающего воздействия
задающего воздействия
![]() ,
а также допустимая ошибка
,
а также допустимая ошибка
![]() .
.
Так
как для низких частот
 ,
то при
,
то при![]() ,
,![]()
![]() .
Тогда
.
Тогда
 .
(9.15)
.
(9.15)
б)
пусть
даны
![]() .
Тогда
.
Тогда
 (9.16)
(9.16)
в)
Пусть для астатической САУ даны
![]() и
и![]() .
.
Тогда
![]() и при
и при![]()
![]() и
и
 . (9.17)
. (9.17)
С
помощью выражений (9.15)–(9.17) строится
низкочастотная область
![]() (рис. 9.6).
(рис. 9.6).

Рис. 9.6
Значение
частоты
![]()
![]() называют добротностью САУ по скорости.
Первый излом
называют добротностью САУ по скорости.
Первый излом![]() на частоте
на частоте![]() при однократном изломе (при изменении
наклона на
при однократном изломе (при изменении
наклона на![]() )
определяется как
)
определяется как ,
где
,
где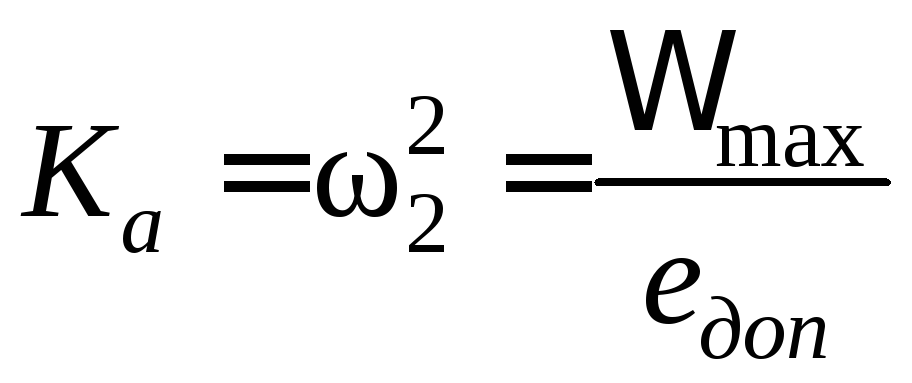
![]() называют добротностью системы по
скорости; при двукратном изломе
называют добротностью системы по
скорости; при двукратном изломе .
.
Учет
требований качества переходного
процесса:
![]() ,
колебатель-
ности, запасов устойчивости.
Эти показатели учитываются при
формировании среднечастотной области
,
колебатель-
ности, запасов устойчивости.
Эти показатели учитываются при
формировании среднечастотной области![]() .
Здесь можно воспользоваться графиками
(рис. 9.7, а, б).
.
Здесь можно воспользоваться графиками
(рис. 9.7, а, б).

Рис. 9.7
По
графику (см. рис. 9.7, а) для заданных
значений
![]() и
и![]() находят
находят![]() и затем из соотношения
и затем из соотношения![]() частоту среза
частоту среза![]() .
.
Например:
(как показано на рис. 9.7, а) для
![]() ,
, ,
откуда для заданного значения
,
откуда для заданного значения![]() (допустим, что оно равно 0,01 с), определяются
значения
(допустим, что оно равно 0,01 с), определяются
значения и
и![]()
По
графику (см. рис. 9.7, б), где установлены
зависимости
![]() от
от![]() и ординат
и ординат![]() и
и![]() среднечастотной части
среднечастотной части![]() от
от![]() ,
находят для заданного значения
,
находят для заданного значения![]() необходимые
необходимые![]() ,
,![]() и
и![]() .
.
Сопряжение среднечастотного участка с низкочастотным и высокочастотным (рис. 9.8) должно быть таким, чтобы была проще коррекция и изломы, по возможности, были однократными.

Рис. 9.8
Для облегчения процедуры синтеза коррекции вводятся типовые передаточные функции исходной системы и соответствующие им передаточные функции желаемой системы:

*
![]() с учётом требований по точности;
с учётом требований по точности;![]()
Остановимся
на коррекции.Вычитая
из
![]() ординаты
ординаты![]() ,
получим
,
получим![]() Вид ЛАХ коррекции соответствует случаю
коррекции с опережением и отставанием
по фазе.
Вид ЛАХ коррекции соответствует случаю
коррекции с опережением и отставанием
по фазе.
Передаточная функция коррекции будет с учётом обеспечения показателей точности иметь вид
 (9.18)
(9.18)
где

![]()
 причём
причём![]() коэффициент
передачи исходной системы.
коэффициент
передачи исходной системы.
Так как реализовать дифференцирующие звенья сложно, переходят к схеме коррекции с использованием интеграторов. Для этого необходимо представить (9.18) в виде


Схема реализации коррекции представлена на рис. 9.9.

Рис. 9.9
9.5. Модальный метод синтеза (метод размещения полюсов)
Рассмотрим
САУ с одним входом и одним выходом, будем
считать
![]() Пусть модель объекта имеет вид
Пусть модель объекта имеет вид
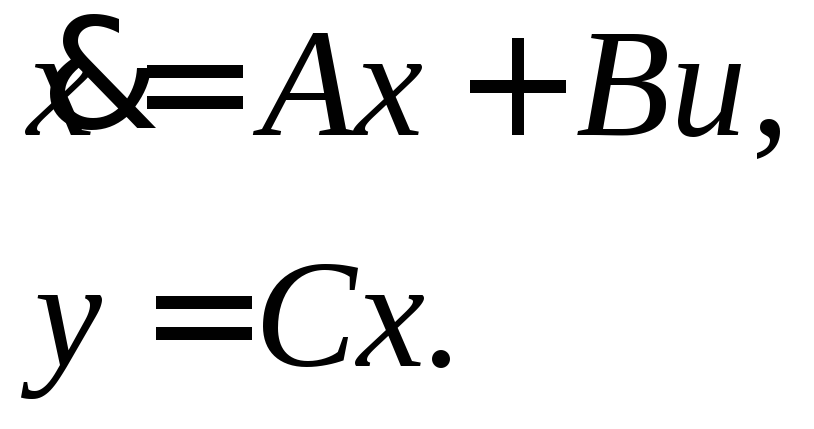 (9.19)
(9.19)
При этом методе синтеза [6] закон управления выражается формулой
![]() (9.20)
(9.20)
где
![]() вектор
коэффициентов
вектор
коэффициентов![]()
Структура замкнутой САУ приведена на рис. 9.10.

Рис. 9.10
Так
как
![]() то
назначение САУ поддерживать значение
то
назначение САУ поддерживать значение![]() Такую САУ называют регулятором состояния.
Такую САУ называют регулятором состояния.
Рассмотрим
пример спутника (рис. 9.11) с передаточной
функцией
![]() [6].
[6].

Рис. 9.11
Модель объекта (спутника) будет иметь вид
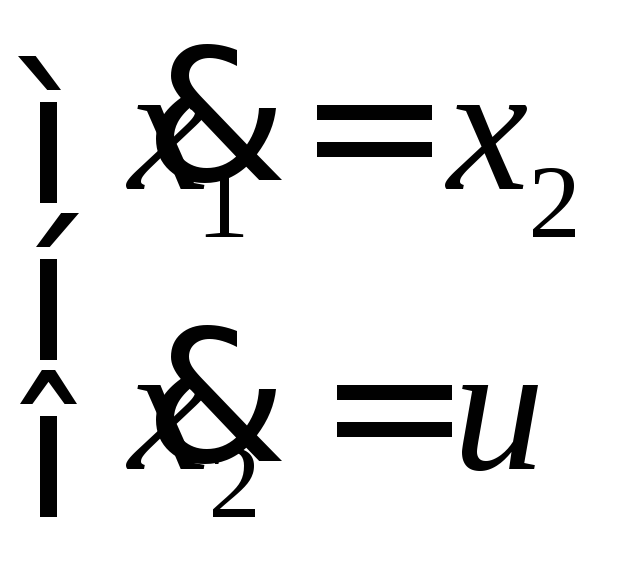 или
или

Для
замкнутой САУ, где
![]() ,
имеем
,
имеем
 или
или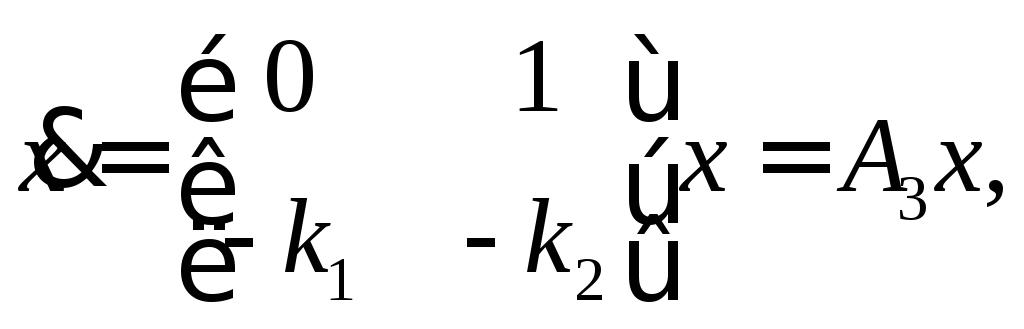 (9.21)
(9.21)
где
![]() матрица коэффициентов замкнутой САУ.
матрица коэффициентов замкнутой САУ.
Характеристическое уравнение замкнутой САУ имеет вид
 (9.22)
(9.22)
Пусть
корни его будут
![]() и
и![]() ,
тогда характеристическое уравнение
желаемой замкнутой системы имеет вид
,
тогда характеристическое уравнение
желаемой замкнутой системы имеет вид
![]() (9.23)
(9.23)
Синтез
системы заключается в выборе
![]() и
и![]() в (9.22), которые бы соответствовали
коэффициентам уравнения (9.23), т.е.
в (9.22), которые бы соответствовали
коэффициентам уравнения (9.23), т.е.
 (9.24)
(9.24)
Рассмотрим общий принцип синтеза САУ.
Пусть
![]()
![]()
![]()
![]() .
.![]()
Подставляя (9.26) в (9.25), получим
![]() (9.27)
(9.27)
Характеристическое уравнение замкнутой САУ имеет вид
![]() (9.28)
(9.28)
Если
корни
![]() то желаемое характеристическое уравнение
замкнутой САУ будет иметь вид
то желаемое характеристическое уравнение
замкнутой САУ будет иметь вид
![]() (9.29)
(9.29)
Приравнивая (9.28) и (9.29), имеем
![]() (9.30)
(9.30)
В
этом уравнении
![]() неизвестных
неизвестных![]() но они могут быть найдены путем
приравнивания коэффициентов при
но они могут быть найдены путем
приравнивания коэффициентов при![]() в одинаковых степенях.
в одинаковых степенях.
Пусть передаточная функция объекта будет иметь вид
 (9.31)
(9.31)
Уравнения
состояния при
![]() имеют вид
имеют вид
 (9.32)
(9.32)
Матрица
![]() является фробениусовой, а уравнение
объекта соответствует нормальной форме.
является фробениусовой, а уравнение
объекта соответствует нормальной форме.
При
законе модального уравнения
![]() для замкнутой САУ в
матрице
для замкнутой САУ в
матрице![]() член
член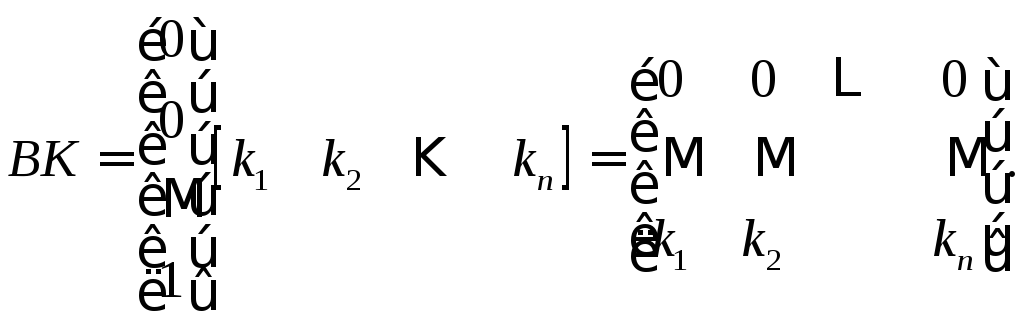 Матрица
Матрица
Характеристическое уравнение замкнутой САУ имеет вид
![]()
Желаемое характеристическое уравнение замкнутой САУ будет
![]()
Из двух последних уравнений следует:


 (9.33)
(9.33)
Последняя
система представляет собой общее решение
задачи синтеза путём размещения полюсов
для САУ с одним входом и одним выходом,
но для этого исходная модель САУ должна
быть в нормальной форме (матрица
![]() фробениусова).
фробениусова).
Аккерман
предложил формулу, которая позволяет
перейти от произвольной формы уравнений
состояния к нормальной, затем найти
![]() а потом перейти к исходной структуре.
а потом перейти к исходной структуре.
Формула Аккермана имеет вид
![]() (9.34)
(9.34)
где
![]() матричный
полином, образованный путём использования
коэффициентов желаемого характеристического
уравнения
матричный
полином, образованный путём использования
коэффициентов желаемого характеристического
уравнения
![]() (9.35)
(9.35)
Последние
выражения (при
![]() )
рассчитываются на компьютере.
)
рассчитываются на компьютере.
Пример
9.3. Для
спутника
 характеристическое уравнение
характеристическое уравнение
![]()
Используем
формулу Аккермана. Определим
 затем
затем![]()
 .
Образуем матричный полином
.
Образуем матричный полином


По
формуле Аккермана

 Как видим, результаты совпали с (9.24).
Как видим, результаты совпали с (9.24).
Остановимся на вопросе формирования полюсов передаточной функции замкнутой САУ, исходя из заданных показателей качества на основе корневых оценок.
Определим
границу расположения желаемых полюсов
(корней) САУ. Исходя из заданного времени
переходного процесса
![]() ,
в силу (7.4) находим
,
в силу (7.4) находим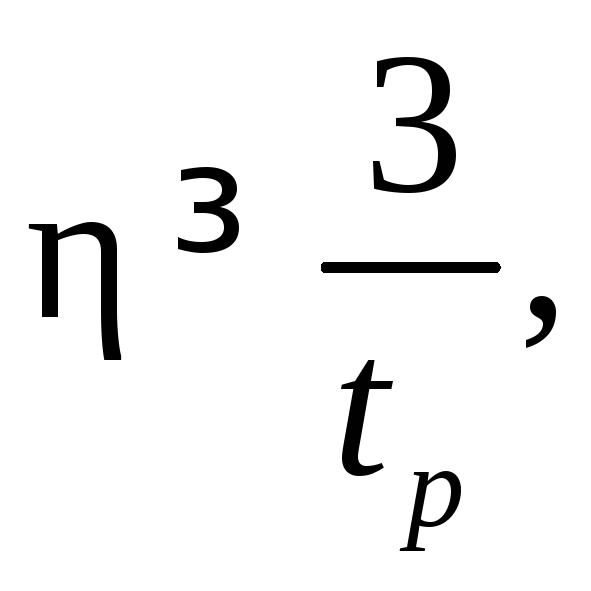 если ближайший к мнимой оси корень
вещественный и
если ближайший к мнимой оси корень
вещественный и![]()
Угол
сектора комплексных корней связан с
перерегулированием в силу (7.6) соотношением
![]() где
где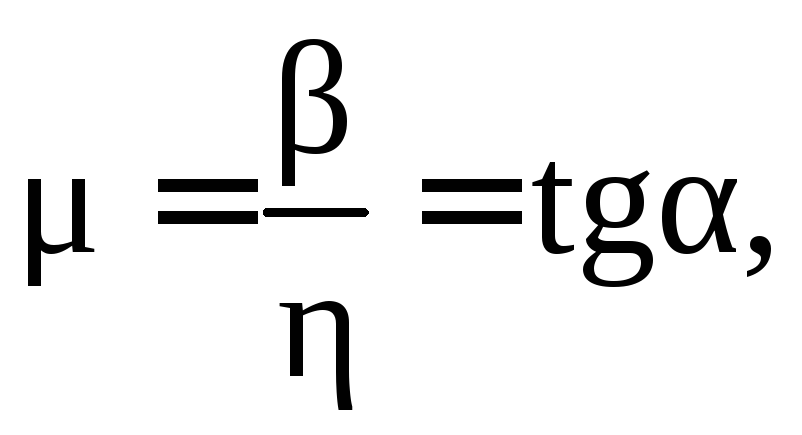 если ближайшая к мнимой
оси – пара
комплексных сопряжённых корней и
если ближайшая к мнимой
оси – пара
комплексных сопряжённых корней и![]()
Из
соотношения
![]() следует
следует
 (9.36)
(9.36)
Пример 9.4. Рассмотрим оба случая для САУ из предыдущего примера.
Если
 (ближайший корень – вещественный) и
(ближайший корень – вещественный) и то
то .
.
Возьмём
оба корня вещественных:
![]() Тогда
Тогда![]()
![]()
![]()
Пусть
 а
а с, т.е.
с, т.е. Тогда
Тогда .
.
При
![]() значение
значение![]() ;
;
![]() ,
,![]()
![]()
![]() .
.
Примечание.
При определении полюсов не следует
чрезмерно увеличивать
![]() ,
так как при этом увеличиваются значения
,
так как при этом увеличиваются значения![]() ,
а для повышения реакции инерционных
объектов надо на их вход подавать большие
сигналы, что может привести к насыщению
элементов и сделать САУ нелинейной [6].
,
а для повышения реакции инерционных
объектов надо на их вход подавать большие
сигналы, что может привести к насыщению
элементов и сделать САУ нелинейной [6].
