1.2. Классификация систем автоматического управления

Классификацию систем автоматического управления осуществляют в зависимости от признаков, в качестве которых могут быть принципы работы, алгоритмы функционирования, структуры систем, вид представления отдельных элементов, вид математических моделей, области применения и др.

По виду алгоритмов функционирования системы автоматического управления делятся на системы стабилизации (V = const, поддерживается некоторое постоянное значение выхода Y, рис. 1.8), системы программного управления (вход V должен изменяться по заданной программе), следящие системы – закон изменения входного сигнала v неизвестен заранее. Примерами таких систем соответственно являются системы стабилизации скорости вращения и частоты; система автоматического управления промышленного робота, работающая в режиме отработки заданных (программных) движений; радиолокационные следящие системы измерения координат движущегося объекта. С развитием практики и теории автоматического управления появляются новые классы систем: системы с поиском экстремума показателя качества, системы оптимального упрaвления, адаптивныe систeмы.

Приведем классификацию систем по виду законов управления. под законом управления будем понимать зависимость выходного сигнала регулятора u от сигнала ошибки e. Для простоты примем, что u и Е – скалярные величины, которые обозначим малыми буквами; тогда в общем случае закон управления будет иметь вид: .

Простейшими случаями этого соотношения являются:

• пропорциональный закон (П-закон):

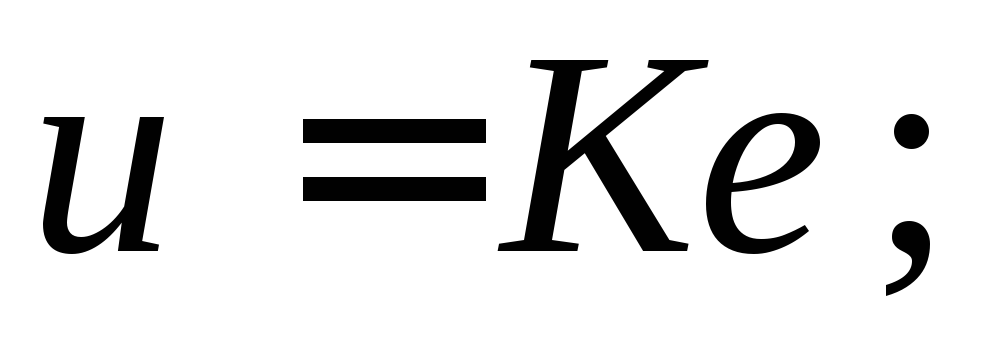
• интегральный закон (И-закон):

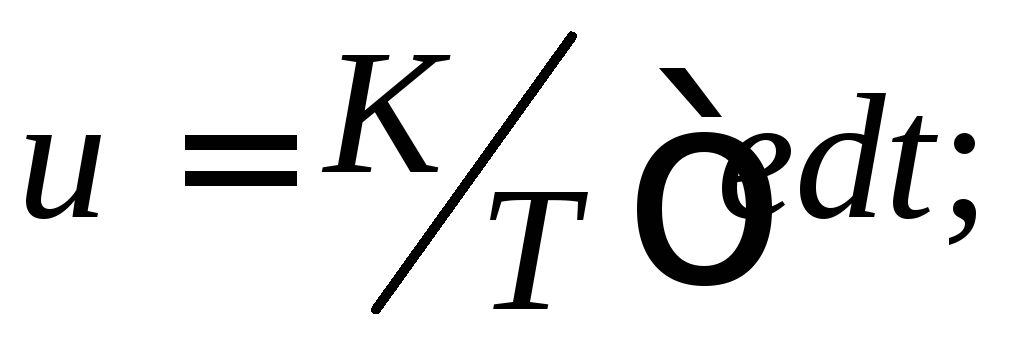
• пропорционально-интегральный закон (ПИ-закон): ;

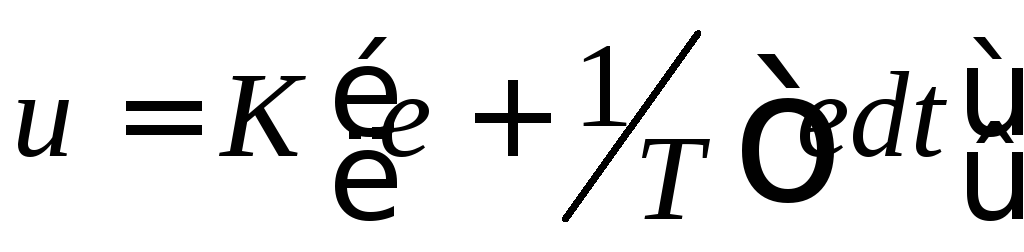• пpопоpционально-интeгально-диффepeнциальный закон (ПИД-закон): ,

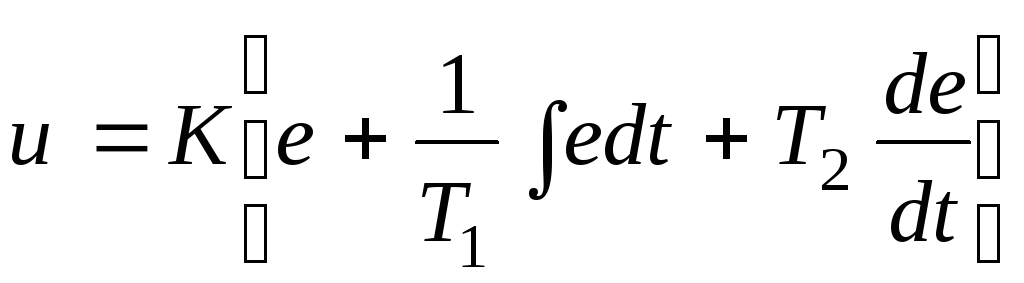где K – коэффициент передачи; а T, T₁, T₂ – постоянные времени.

По количеству управляемых координат системы делятся на одномерныe () имногомеpныe, или многосвязныe () (см. рис. 1.1).

По характеру протекающих процессов системы делятся на непрерывные (все сигналы непрерывны во времени) и импульсные (хотя бы один из сигналов дискретизирован (квантован) во времени). Если хотя бы один из сигналов в системе является квантованным по уровню, то она относится к релейным системам. При одновременном квантовании сигнала по уровню и времени систему относят к цифровым. Релейные, импульсные и цифровые системы составляют класс дискретных систем автоматического управления.

По зависимости выходных сигналов отдельных элементов от входных системы делятся на линейные и нелинейные.

По виду параметров, характеризующих отдельные элементы и устройства, системы делятся на системы с сосредоточенными или распределенными параметрами, стационарные (все параметры постоянны во времени), нестационарные (параметры изменяются во времени), системы с детерминированными параметрами (закон изменения параметров известен), со случайными (стохастическими) параметрами (заданы их вероятностные характеристики), с неопределенными параметрами (может, например, задаваться только область их изменения).

Приведенная классификация не охватывает всех классов существующих систем. Например, можно выделять еще системы с запаздыванием, системы с перестраиваемой структурой. Адаптивные системы делятся на самонастраивающиеся и самоорганизующиеся.