7. Оценки качества переходных процессов

Численные величины, характеризующие работу системы автоматического управления, носят название показателей качества, которые условно можно разделить на три группы: характеризующие а) устойчивость системы, б) точность системы и в) качество переходных процессов. Обеспечение устойчивости является необходимым условием функционирования любой системы управления и гарантирует затухание свободной или переходной составляющей процесса. К этой первой группе показателей относятся запасы устойчивости по амплитуде и фазе.

После затухания свободной составляющей через достаточно большой промежуток времени в системе протекает установившийся процесс, который обуславливает точность системы. Показателями качества в данном случае выступают величины ошибок в установившемся режиме, которые рассмотрены в разд. 6 (вторая группа).

Наконец, к третьей группе относятся показатели качества переходного процесса, которые характеризуют вид процесса для достаточно малых моментов времени после его начала. Среди таких показателей – время регулирования , перерегулированиеи ряд других, приведенных в подразд. 4.1.

Показатели качества могут быть вычислены двумя способами. Первый –непосредственно по виду переходного процесса. В этом случае их называют прямыми оценками качества. Второй способ – это использование косвенных оценок показателей качества без построения кривой переходного процесса.

В данном разделе рассмотрим наиболее распространенные косвенные методы оценки показателей качества переходного процесса.

7.1. Корневые оценки качества

Переходная функция замкнутой системы как реакция системы на единичный скачок по положению вычисляется в соответствии с выражением (4.11), в котором второе слагаемое в виде суммы определяет переходную составляющую

, (7.1)

a – различные корни характеристического уравнения замкнутой системы.

Если ,, то, т.е. с течением времени переходная составляющая затухает.

В выражении (7.1) перейдем к модулям в левой и правой частях:

, (7.2)

где .

Обозначим расстояние от мнимой оси до ближайших действительного корня (рис. 7.1, а) или пары комплексно-сопряженных корней (рис. 7.1, б) на плоскости корней через .

Рис. 7.1

Величину будем называтьстепенью устойчивости. Очевидно, что . Так как, то для любого множителяв (7.2) будет справедлива оценка. Таким образом, (7.2) равносильно выражению

, а . (7.3)

Из (7.3) следует, что переходная составляющая затухает быстрее, чем экспонента с показателем –. Если принять время регулированиякак время, начиная с которого войдет в 5 % трубку от начального значения, то из (7.3) получим , откуда

. (7.4)

Выражение (7.4) и соответственно величина характеризуют предельное быстродействие системы, поэтому иногда величину называют еще мерой быстродействия системы.

Из рассмотренного выше следует, что доминирующее влияние на характер переходного процесса оказывают ближайшие к мнимой оси корни. Если ближайшими являются комплексно-сопряженные корни , то наряду со степенью устойчивости вводят в рассмотрениеколебательность системы (колебательность переходного процесса) . Паре комплексно-сопряженных корней в (7.1) соответствует составляющая

, (7.5)

где ,– комплексно-сопряженные величины;A, – действительные величины.

Составляющая (7.5) носит колебательный характер. Период колебания определяется величиной . Уменьшение амплитуды в (7.5) за периодТ будет равно , т.е. определяться величиной.

Перерегулирование в % может быть оценено по формуле

. (7.6)

С увеличением увеличивается число колебаний за время регулирования и возрастает перерегулирование. Величинаносит качественный характер и является оценкой переходного процесса сверху, поэтому в действительности переходной процесс может иметь лучшие показатели.

Характер переходного процесса в значительной степени зависит от корней характеристического уравнения, т.е. от полюсов передаточной функциизамкнутой системы. Однако на величину амплитуды переходных составляющих будут влиять и нули передаточной функции. Пусть полиномN(s) имеет m нулей , тогдаи выражение (7.1) примет вид.

Очевидно, если какой-то полюс будет близок (или в идеальном случае равен) нулю передаточной функции, то составляющая, соответствующая корню , будет мала по амплитуде (или равна нулю).

Впервые корневые оценки качества переходных процессов для систем третьего порядка были предложены в работе И. А. Вышнеградского (1876), положившей начало развитию теории автоматического управления.

Характеристическое уравнение системы третьего порядка путем замены переменной приводится к виду

, (7.7)

где ,,.

Коэффициенты А, В – параметры Вышнеградского – являются комбинацией коэффициентов и в конечном итоге зависят от реальных параметров системы. Условие асимптотической устойчивости для уравнения (7.7) несложно получить с помощью критерия Гурвица, оно имеет вид АВ > 1. В области устойчивости, ограниченной гиперболой АВ = 1 в плоскости параметров А, В, нанесем кривые, разделяющие область устойчивости на области с одинаковым расположением корней характеристического уравнения (7.7).

На рис. 7.2 представлена диаграмма Вышнеградского, где для каждой области показано расположение корней и вид переходного процесса.

Таким образом, выбирая из диаграммы требуемый вид переходного процесса, можно найти необходимые значения параметров А, В или .

В заключение отметим ряд простых случаев, когда получены оценки степени устойчивости и соответственно быстродействия системы. Рассмотрим систему управления стандартной структуры, изображенной на рис. 3.1. Пусть передаточная функция объекта управленияимеет вид, где.

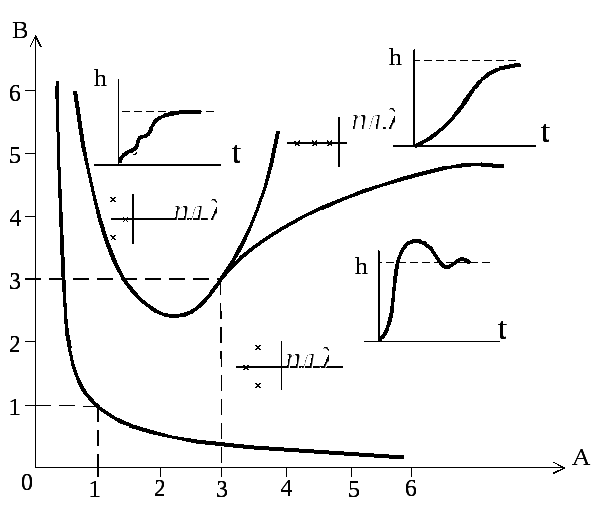
рис. 7.2

Передаточную функцию будем рассматривать как передаточную функцию регулятора (управляющего устройства). Рассмотрим три случая закона управления: интегральный, пропорциональный, пропорционально-интегральный. Быстродействие объекта управления может быть охарактеризовано величиной. Доказано, что для интегрального закона управления быстродействие замкнутой системы, характеризуемое величиной степени устойчивости, не будет превосходить быстродействия объекта, т.е..

Для пропорционального и пропорционально-интегрального законов управления быстродействие замкнутой системы управления может превосходить быстродействие объекта управления, но будет ограничено неравенством .

Приведенный частный результат распространяется на более общий случай: астатические системы уступают по быстродействию системам статическим.

Пример 7.1. Пусть передаточная функция разомкнутой системы имеет вид . Характеристическое уравнение замкнутой системыимеет корни.

Если , то имеем два комплексно-сопряженных корня и ,,.

Если , то имеем два действительных корня и ,,.

Из приведенных соотношений следует, что при процессы в системе будут носить колебательный характер, а быстродействие системы будет ограничено величиной 6Т. При процессы носят апериодический характер, но быстродействие в системе уменьшается.