6.2. Установившиеся ошибки при произвольном входном сигнале

Обозначим весовую функцию замкнутой системы по ошибке через . Тогда соотношениюво временной области будет соответствовать свертка.

Так как нас интересует установившаяся ошибка после затухания переходной составляющей, то отнесем нижний предел интегрирования, соответствующий моменту подачи входного сигнала, в . В этом случае получим выражение, справедливое для установившегося значения сигнала ошибки: .

Заменив переменную интегрирования , получим

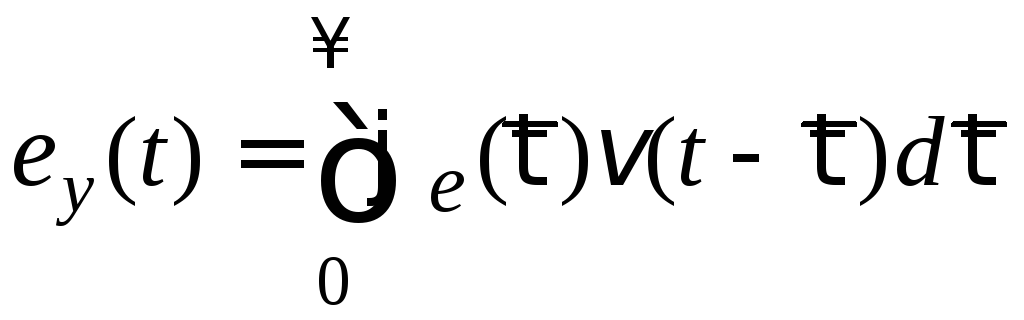. (6.7)

Полагая функцию аналитической, разложим ее в ряд Тейлора при: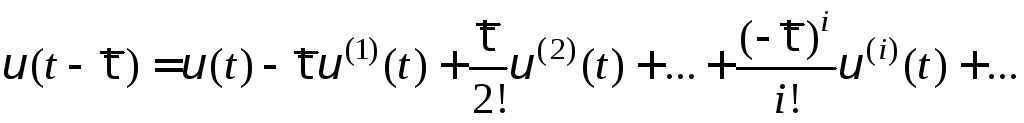и подставим полученный ряд в (6.7). В результате получим

, (6.8)

где коэффициенты определяются выражением.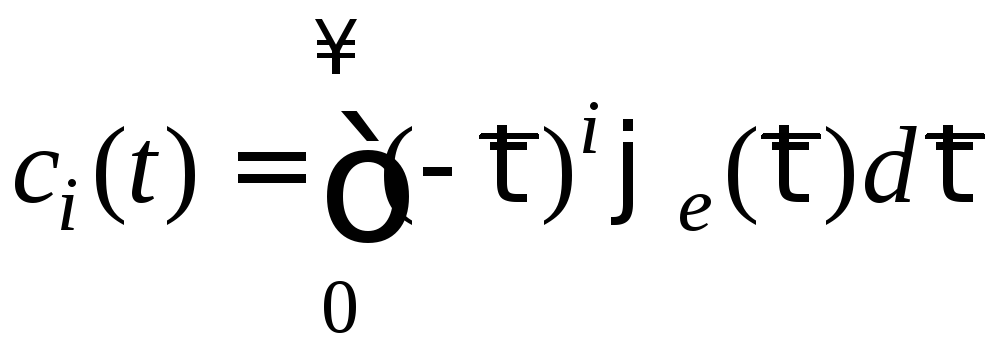

Так как передаточная функция замкнутой системы по ошибке есть прямое преобразование Лапласа от весовой функции 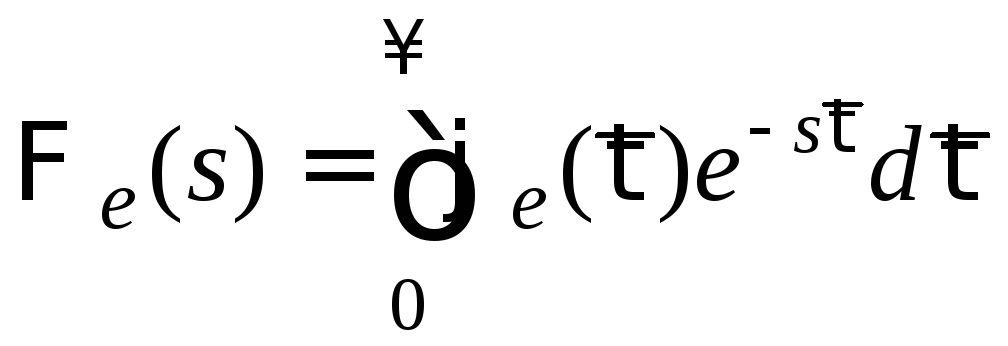, то очевидно соотношение

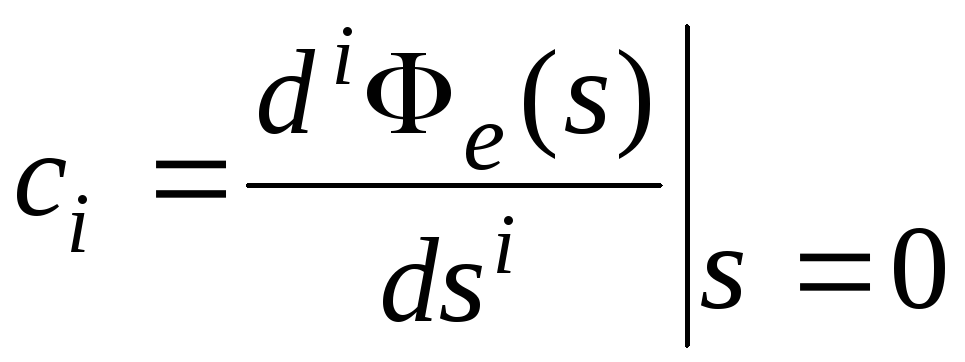. (6.9)

Коэффициенты носят названиекоэффициентов ошибок и характеризуют, с каким весом функция и ее производные входят в общее выражение для установившейся ошибки (6.8). Если входной сигнал изменяется достаточно медленно, то в выражении (6.8) можно ограничиться конечным числом членов ряда.

Если , то. В статической системе и , для системы с астатизмом первого порядка имееми, а

Аналогично можно показать, что для астатической системы с астатизмом -го порядка,.

Коэффициент называют коэффициентом статической ошибки,– коэффициентом скоростной ошибки,– коэффициентом ошибки по ускорению. Из (6.8) следует, что если, то , если, то.

В общем случае формула (6.9) редко используется для вычисления . На практике применяется другой способ. Разложим передаточную функциюв ряд Маклорена приs = 0:

. (6.10)

С другой стороны, так как 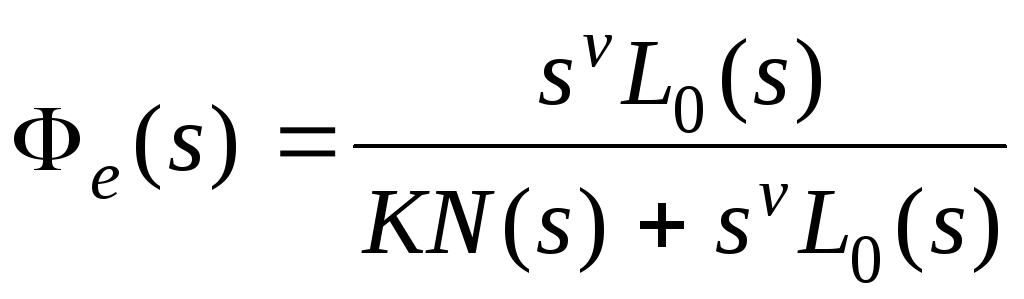есть отношение полиномов, то деля полином числителя на полином знаменателя, получим ряд

. (6.11)

Приравнивая коэффициенты при одинаковых степенях s в (6.10), (6.11), получим

. (6.12)

Величина коэффициентов ошибок в конечном итоге определяет величину ошибки в системе. Из изложенного выше вновь следует, что величины будут тем меньше, чем выше порядок астатизма системы и чем больше величина коэффициента усиленияK разомкнутой системы.

Пример 6.2. Пусть передаточная функция разомкнутой системы имеет вид . Найдем первые три коэффициента ошибок. Передаточная функция замкнутой системы по ошибке будет равна. Деля полином числителя на полином знаменателя, получим.

В соответствии с (6.12) найдем ,,.

Определим установившуюся ошибку в системе при воздействии . Подставляя найденные значенияи заданные значения функциии ее производных в (6.8), получим.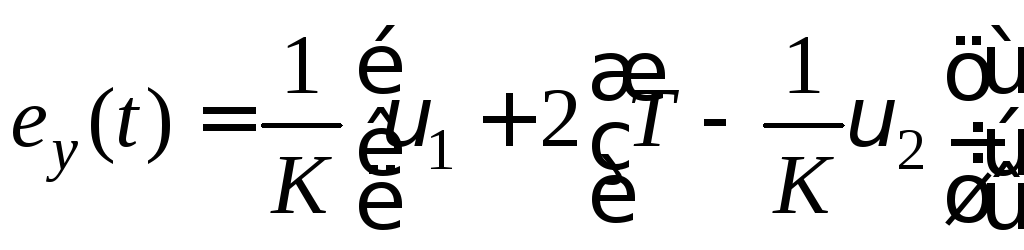

6.3. Установившиеся ошибки при гармоническом воздействии

Если главная передаточная функция замкнутой системы имеет вид , то при входном сигналевыходной сигнал в установившемся режимебудет определяться выражением

, (6.13)

где ,.

Аналогично, зная , можно найти закон изменения ошибки в установившемся режиме при гармоническом входном сигнале:

, (6.14)

где .

Выражения (6.13), (6.14) позволяют оценить ошибки воспроизведения гармонического сигнала в установившемся режиме. Из этих выражений следует, что кроме ошибки воспроизведения амплитуды входного гармонического сигнала существуют и постоянные фазовые ошибки, которые определяются видом фазочастотных характеристик замкнутой системы. Обычно при анализе точности систем управления их не рассматривают, ограничиваясь лишь анализом ошибок воспроизведения амплитуды.

Из (6.13), (6.14) можно получить ошибки воспроизведения амплитуды гармонического сигнала на заданной частоте, равные

, (6.15)

, (6.16)

первая из которых характеризует разность между максимальными значениями амплитуды входного и выходного сигналов, а вторая – максимальную величину ошибки . Очевидно, всегда. Так както. Если, то. Таким образом, при малых фазовых сдвигах на заданной частоте оценки (6.15) и (6.16) будут близки между собой. Это обычно выполняется в диапазоне низких частот.

На рис. 6.2 представлен типичный вид АЧХ замкнутой системы для случая астатической системы, при этом. В случае статической системы. На рисунке заштрихованная область соответствует величинам ошибок.

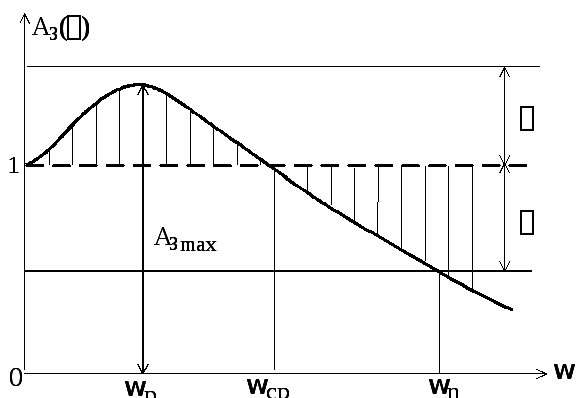
Рис. 6.2

Под полосой пропускания системы понимают диапазон частот , при котором ошибкабудет меньше некоторой заданной, т.е.. Иногда полосу пропускания определяют как диапазон частот, при котором выполняется условие.

Полоса пропускания является важной характеристикой системы. С одной стороны, чем шире полоса пропускания, тем с меньшими ошибками система воспроизводит управляющие сигналы. Однако, с другой стороны, увеличение приводит к тому, что система становится чувствительной к влиянию высокочастотных помех.

Из выражения (6.16) можно получить приближенные оценки величины ошибки . Так как, то для статической системыи при достаточно низких частотах можно полагать,,, откуда имеем

. (6.17)

Для астатической системы и при низких частотах, откуда получим

. (6.18)

Если выполняется условие , то формула (6.18) принимает вид

. (6. 19)

Из (6.17)–(6.19) видно, что ошибка системы обратно пропорциональна коэффициенту усиления разомкнутой системы.

Итак, для повышения точности САУ следует увеличивать коэффициент усиления разомкнутой системы либо увеличивать порядок астатизма. Однако это будет приводить в общем случае к ухудшению устойчивости. Таким образом, требования к точности системы и ее устойчивости являются противоречивыми.

Пример 6.3. Пусть передаточная функция разомкнутой системы имеет вид 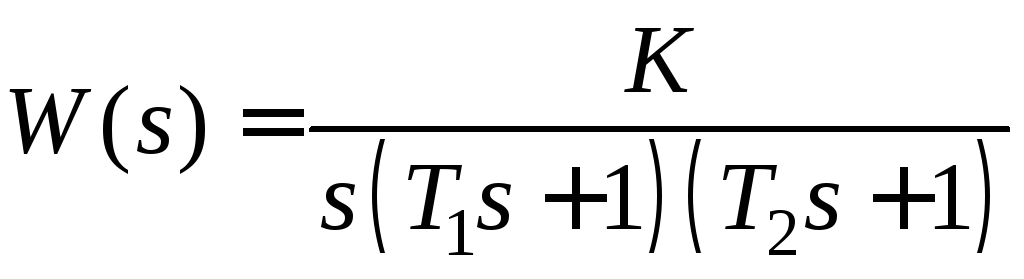при, с, с,с^-1.

Передаточная функция системы по ошибке . Находим величину(6.16):с^-1. Если воспользоваться приближенной формулой (6.19), то с^-1, т.e. с точностью до третьего знака оба результата совпадают.