5.2. Алгебраические критерии устойчивости

К алгебраическим критериям устойчивости относят те, которые позволяют судить об устойчивости системы по коэффициентам уравнения (5.2). необходимым условием устойчивости линейной системы (5.1) является положительность коэффициентов характеристического уравнения (5.2), т.е.

. (5.3)

Докажем этот критерий. Пусть уравнение (5.2) имеет n корней , тогда полиномможно пo теореме Безу представить в виде . Если, то произведениеn сомножителей всегда даст полином n-й степени с положительными коэффициентами, и с учетом получим (5.3).

Критерий является лишь необходимым, т.е. если среди есть отрицательные коэффициенты, то система неустойчива; если всеположительны, то система может быть как устойчивой, так и неустойчивой. В этом последнем случае требуется дальнейшее исследование.

Рассмотрим критерий, дающий необходимые и достаточные условия устойчивости, предложенные немецким ученым А. Гурвицем в 1895 году. Предварительно из коэффициентов уравнения (5.2) сформируем матрицу Гурвица:

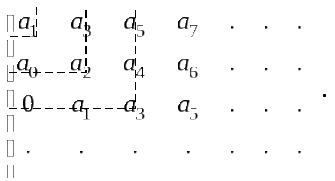
(5.4)

Алгоритм ее формирования следующий. Сначала по главной диагонали слева направо выписываем коэффициенты . Далее столбцы вверх от главной диагонали дополняются коэффициентами с возрастающими индексами, а вниз – с убывающими индексами. Коэффициенты с индексами большеn и меньше нуля заменяются нулями. Последний столбец матрицы имеет все нулевые коэффициенты, кроме последнего . Обозначим через главные определители матрицы Гурвица, которые выделены в (5.4) штриховыми линиями:,где –определитель матрицы Гурвица.

Критepий Гуpвица. Необходимым и достаточным условием устойчивости линейной системы является при положительность всех определителей Гурвица:

. (5.5)

Для систем до 4-го порядка включительно, раскрывая определители Гурвица, можно получить необходимые и достаточные условия устойчивости:

(5.6)

(5.7)

; (5.8)

(5.9)

Из (5.6), (5.7) следует, что для системы первого и второго порядка необходимые условия совпадают с необходимыми и достаточными, а при n = 3 и 4 кроме необходимых условий следует соблюдать дополнительное неравенство. При n = 5 и 6 появляются два дополнительных неравенства, при n = 7 и 8 – три и т.д. при аналитических исследованиях критерий Гурвица наиболее удобен для систем, порядок которых .

С помощью критерия Гурвица можно определить границы устойчивости. Если и все определители Гурвица, кроме последнего, больше нуля, то нарушение условий устойчивости будет при, откуда приполучаем границу устойчивости апериодического типа (появляется один нулевой корень), а приграницу устойчивости колебательного типа (появляются два комплексно-сопряженных корня). При этом все остальные корни являются левыми. Граница устойчивости, соответствующая бесконечному корню, будет.

Одним из частных случаев критерия Гурвица является критерий Льенара–Шипара (1914), по которому для устойчивости системы необходимо и достаточно выполнение следующих неравенств:

или

,

т.е. при соблюдении необходимых условий устойчивости требуется положительность четных или нечетных определителей Гурвица.

Вторым распространенным алгебраическим критерием устойчивости, дающим необходимые и достаточные условия устойчивости, является критерий Рауса–Гурвица. Этот критерий более удобен при анализе устойчивости с помощью ПЭВМ.

На первом этапе составляется таблица Рауса, элементы которой образуются из коэффициентов характеристического полинома замкнутой системы , в которой.

Таблица Рауса:

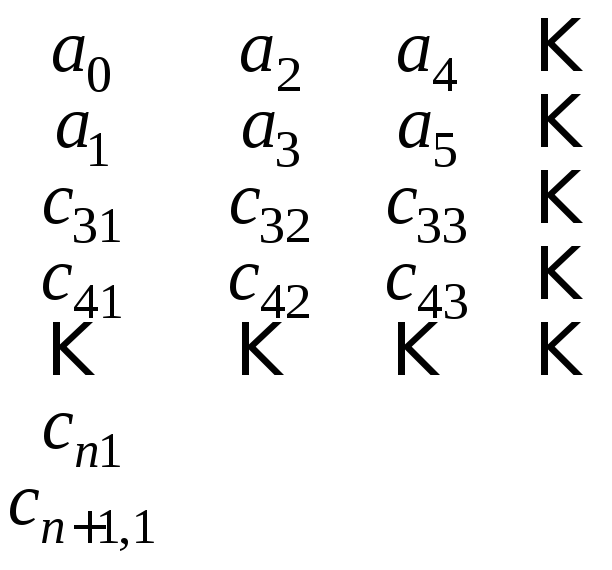(5.10)

Первые две строки состоят из коэффициентов .

Коэффициенты последующих строк вычисляются так:

(5.11)

; ; …

; ; …

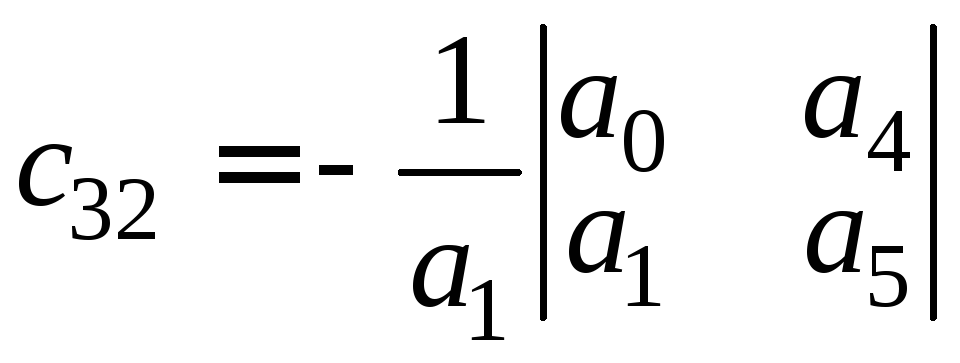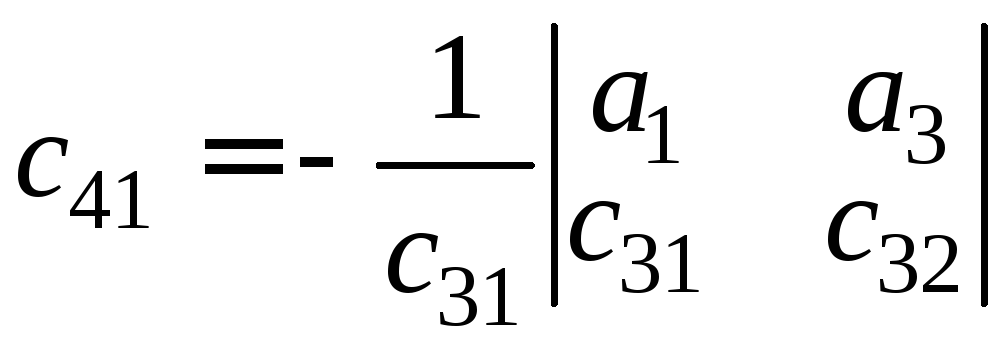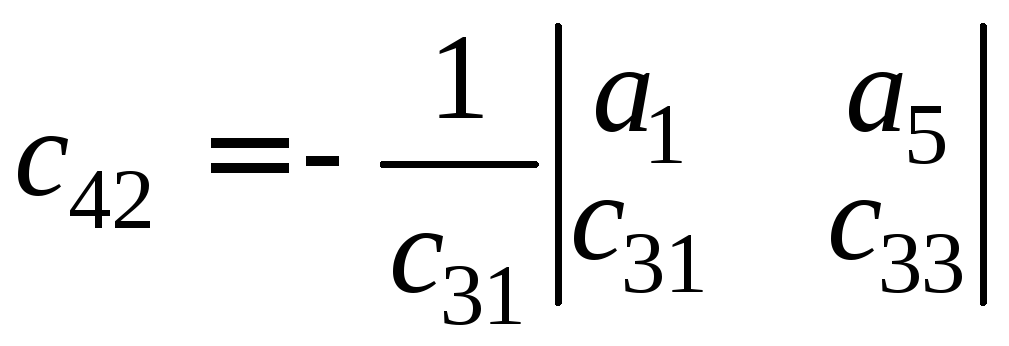и т.д.

Левый столбец записывается для наглядности.

По критерию Рауса–Гурвица система устойчива, если при положительны все элементы первого столбца таблицы (,,,…).

Число правых корней в случае неустойчивой САУ равно числу перемен знака элементов первого столбца. Если элемент какой-то строки первого столбца равен нулю, то САУ либо неустойчива, либо находится на границе устойчивости [6].

Пример 5.1. Рассмотрим замкнутую систему управления, у которой передаточная функция разомкнутой системы W(s) имеет порядок не выше второго () и определяется одним из перечисленных выражений:

, ,,,.

Характеристическое уравнение замкнутой системы для соответствующей разомкнутой будет иметь следующий вид: , ,,. Если параметры, то в соответствии с (5.6), (5.7) замкнутая система будет асимптотически устойчивой для всех передаточных функций, кроме.в этом случае замкнутая система будет находиться на границе устойчивости, так как характеристическое уравнение имеет чисто мнимые корни(коэффициенти условие (5.7) не выполняется).

Пример 5.2. Пусть передаточная функция разомкнутой системы

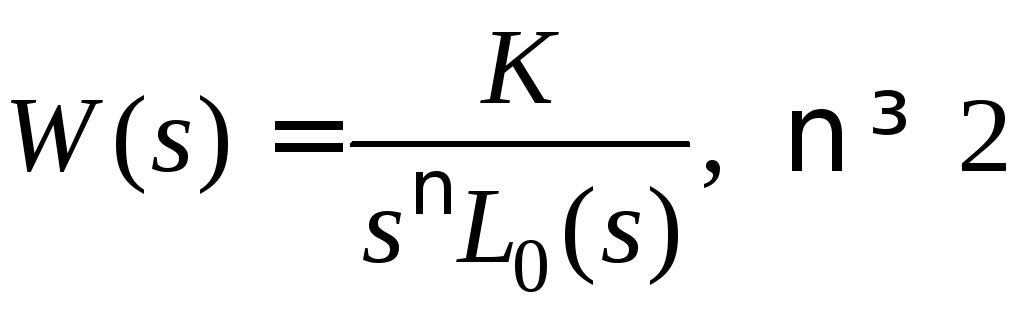, а .

Характеристическое уравнение замкнутой системы будет , из которого следует, что приряд коэффициентов характеристического уравнения(при),и(при) и т.д. равен нулю. В этом случае не выполняется необходимое условие устойчивости (5.3) и система ни при таких значениях параметровK и не может быть асимптотически устойчивой. Такой класс систем называютстpуктуpно нeустойчивыми.

Пример 5.3. Передаточная функция разомкнутой системы задана в виде . Характеристическое уравнение будет. Используя (5.8), найдем условие устойчивости системы в виде,,,, из которого следуют неравенства,,,.

Таким образом, при заданных имаксимальное значение коэффициента усиления ограничено и увеличение приведет к потери устойчивости. Это свойство, как будет показано дальше, является весьма характерным для систем автоматического управления и в общем случае. Система будет находиться на границе устойчивости, если выполняется одно из соотношений:,,,.