3. Найбільш вживані числові множини

Нехай . Будемо використовувати наступні позначення:

відрізок,

інтервал,

півінтервал,

півінтервал.

Указані множини ще називають проміжками. Ми розглядатимемо також і нескінченні множини, використовуючи для цього символи .

Околом точки називається довільний інтервал , який містить точку , тобто .

Інтервал називається околом точки . Точка називається центром цього околу, а число його радіусом. Зазвичай так позначають околи з центром у точці і дуже малим радіусом, тобто коли досить мале.

4. Межі числових множин

Нехай задано непорожню числову множину .

Множина називається обмеженою зверху, якщо існує таке дійсне число, що для кожноговиконується нерівність

Множина називається обмеженою знизу, якщо існує таке дійсне число, що для кожноговиконується нерівність

При цьому числа іназиваються відповідно верхньою та нижньою межею множини.

Множина, яка обмежена зверху й знизу, називається обмеженою.

Очевидно, що будь-яка обмежена зверху (знизу) множина має безліч верхніх (нижніх) меж.

Найменша верхня межа обмеженої зверху множини називається точною верхньою межею або верхньою гранню цієї множини і позначається(supremum(лат.) – найвище).

Найбільша нижня межа обмеженої знизу множини називається точною нижньою межею або нижньою гранню цієї множини і позначається(infimum(лат.) – найнижче).

Якщо , то для довільного числаіснуєтаке, що. Якщо, то для довільного числаіснуєтаке, що.

Теорема.Будь-яка непорожня обмежена зверху числова множина має точну верхню межу. Якщо ж вона обмежена знизу, то має точну нижню межу.

Доведення.Нехай– непорожня обмежена зверху числова множина. Тоді множиначисел, які обмежуютьзверху, непорожня. Із означення верхньої межі випливає, щовиконується нерівність. За аксіомою неперервності дійсних чисел існує таке число, щовиконується нерівність.

Із цієї нерівності випливає, що обмежуєзверху, тобто є верхньою межею, і є найменшим із усіх верхніх меж, тобто є точною верхньою межею.

Друга частина теореми доводиться аналогічно.

Якщо множина не обмежена зверху ( знизу ), то за домовленістю пишуть.

5. Абсолютна величина числа

Абсолютною величиною (модулем) числаназивається саме число, якщо, число –, якщо.

Абсолютна величина числа позначається символом.

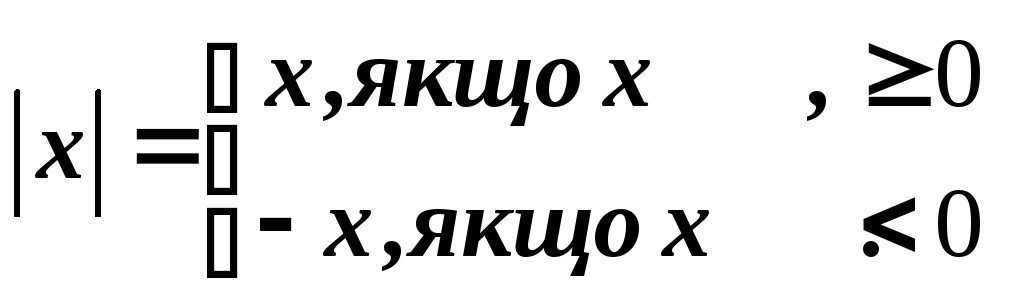
Із означення абсолютної величини випливає, що нерівності і, дерівносильні, тобто.

Теорема.Абсолютна величина суми двох чисел не більше від суми абсолютних величин чисел, тобто.

Доведення.За означення абсолютної величини

для будь-яких чисел . Додаючи почленно ці нерівності, одержимо

.

Остання нерівність рівносильна нерівності

.

Теорема.Абсолютна величина різниці двох чисел не менше від різниці абсолютних величин чисел, тобто

.

Доведення.Для будь-яких чиселмаємо

За попередньою теоремою

.

Звідси одержуємо

.

Зазначимо, що мають місце співвідношення

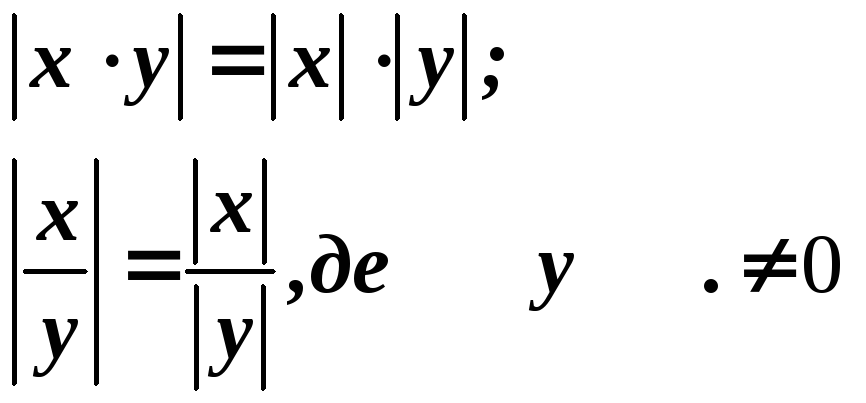
Тема 2. Числові послідовності

ЛЕКЦІЯ 5

1. Означення числової послідовності.

2. Арифметичні дії над числовими послідовностями.

3. Обмежені і необмежені числові послідовності.

4. Нескінченно малі і нескінченно великі послідовності.

5. Основні властивості нескінченно малих послідовностей.