3. Теорема Больцано-Вейєрштрасса

Теорема.Із будь-якої обмеженої послідовностіможна виділити збіжну підпослідовність.

Доведення.Нехай послідовністьобмежена, тобто існує такий відрізок, що для всіхвиконується нерівність. Поділимо відрізокпополам. Тоді принаймні в одній половині буде міститися нескінченна множина елементів послідовності. Позначимо цю половину. Поділимо тепер відрізокна два рівних відрізки і знову виберемо той із них, у якому міститься нескінченна множина елементів послідовності. Позначимо його. Продовжуючи цей процес, дістанемо послідовність укладених відрізків

,

у яких довжина -го відрізка 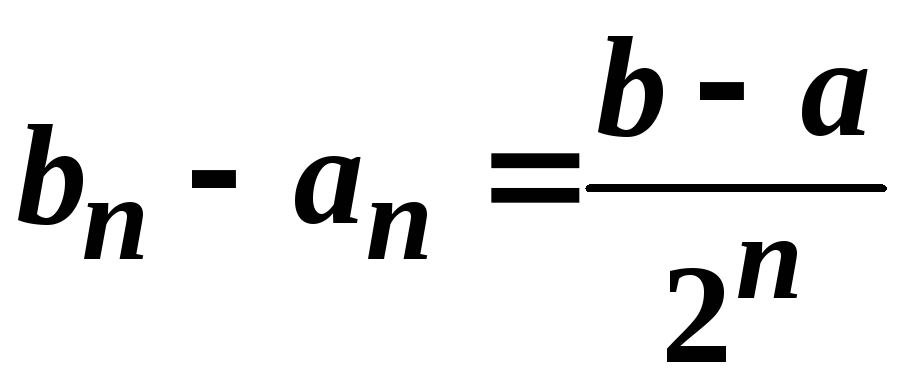прямує до нуля при. Отже, за теоремою про вкладені відрізки.

Побудову підпослідовності послідовностівиконаємо так: у значеннівиберемо довільний елемент із, який належить відрізку, у значеннідовільний елемент із, котрий належить відрізкуі т. д. Оскільки для вибраних таким чином елементів виконується нерівність, то за теоремою 2.7.

4. Критерій Коші збіжності числової послідовності.

Означення границі числової послідовності не дає змоги встановлювати збіжність чи розбіжність числової послідовності, якщо не задано значення самої границі. Воно лише дає можливість перевіряти, чи є число границею даної послідовності, чи ні. Отже, виникає необхідність у наявності критерію збіжності числової послідовності, у якому б саме значення границі було відсутнє, тобто щоб цей критерій виявив "внутрішню" структуру збіжної послідовності. Такий критерій був установлений чеським математиком Больцано і французьким математиком Коші. Нині він має назву критерію Коші.

Теорема.Для того, щоб числова послідовністьбула збіжною, необхідно і достатньо, щоб для будь-якого числаіснував номертакий, що нерівність

(7)

виконувалася б для всіх , які одночасно задовольняють умову.

Доведення.Необхідність. Нехай послідовністьзбіжна і. Задамо довільне число. За означенням границі існує такий номер, що

(8)

для всіх . Зрозуміло, що коли, то для всіх такихнерівність (8) виконується. Отже, нехай. Тоді

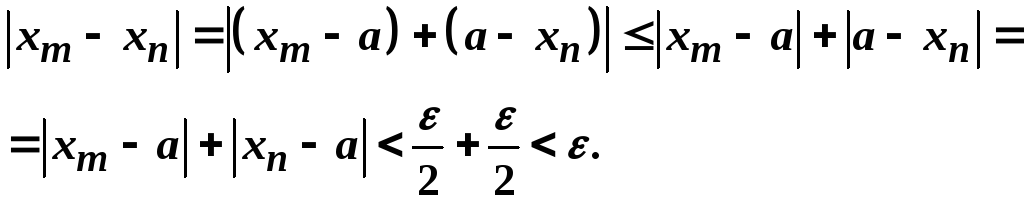
Необхідність доведено.

Достатність. Нехай для будь-якого існує номер, такий, щодля всіх, які одночасно задовольняють умову. Доведемо, що при цьому послідовністьзбіжна. Нехай заданомувідповідає номер, для якого виконується нерівність (7) для всіх. Зафіксуємо одне із значень. Тоді за умовою (7) виконуються нерівності

тобто всі члени послідовності, починаючи з , знаходяться воколі фіксованої точки. Звідси випливає, що послідовністьобмежена. Отже, згідно з теоремою Больцано-Вейєрштрасса, із неї можна виділити збіжну підпослідовність. Нехай. Тодіє також границею послідовності. Дійсно,можна вибрати настільки великим, щоб одночасно виконувались нерівності. Тоді, поклавши, матимемоі. Звідси одержуємо

для всіх . А це означає, що.

Послідовність називається фундаментальною або послідовністю Коші, якщо для будь-якого числаіснує номертакий, що для всіх, котрі одночасно задовольняють умову, виконується нерівність.

ЛЕКЦІЯ 9

17. Поняття метричного простору.

18. Повні метричні простори. Теорема Бера.

19. Доповнення простору.