
- •Тема 1. Вступ. Дійсні числа
- •1. Вступ
- •2. Елементи теорії множин
- •1. Поняття відображення або функції
- •2. Потужність множин
- •3. Зчисленні множини
- •4. Математична індукція
- •1. Дійсні числа
- •1. Аксіоми додавання і множення
- •2. Аксіоми порівняння дійсних чисел
- •2. Деякі властивості дійсних чисел
- •Із означення множини дійсних чисел випливає, що ця множина впорядкована.
- •1. Поняття ізоморфізму
- •2. Інтерпретація множини дійсних чисел
- •3. Найбільш вживані числові множини
- •4. Межі числових множин
- •5. Абсолютна величина числа
- •Абсолютна величина числа позначається символом.
- •Тема 2. Числові послідовності
- •1. Означення числової послідовності
- •1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…,
- •2. Арифметичні дії над числовими послідовностями Нехай задано послідовності і.
- •2. Обмежені і необмежені числові послідовності
- •4. Нескінченно малі і нескінченно великі послідовності.
- •5. Основні властивості нескінченно малих послідовностей
- •1. Збіжні послідовності
- •2. Властивості збіжних послідовностей
- •3. Невизначені вирази.
- •1. Граничний перехід у нерівностях
- •2. Монотонні послідовності
- •3. Число е
- •4. Теорема про вкладені відрізки.
- •1. Теорема про вкладені відрізки.
- •3. Теорема Больцано-Вейєрштрасса
- •4. Критерій Коші збіжності числової послідовності.
- •1. Поняття метричного простору
- •2. Повні метричні простори.
- •3. Доповнення простору.
- •Тема 3. Границя функції однієї змінної
- •1. Границя функції. Означення границі функції за Гейне й за Коші.
- •2. Односторонні границі
- •3. Границя функції на нескінченності
- •4.Теореми про границі функцій
- •1. Визначні границі
- •2. Нескінченно малі й нескінченно великі функції
- •3. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
- •Тема 4. Неперервні та рівномірно неперервні функції
- •1. Неперервність функції в точці
- •2. Операції над неперервними функціями
3. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
Нехай
![]() і
і![]() нескінченно малі в точці
нескінченно малі в точці![]() функції. Якщо
функції. Якщо ,
то говорять, що
,
то говорять, що![]() в околі точки
в околі точки![]() є нескінченно малою вищого порядку
порівняно з
є нескінченно малою вищого порядку
порівняно з![]() ,
і пишуть
,
і пишуть![]() .
.
Якщо
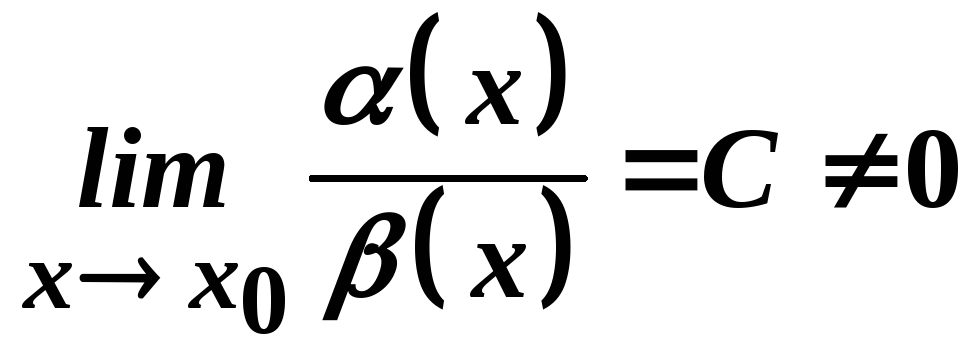 ,
де
,
де![]() ,
то функції
,
то функції![]() і
і![]() називаються нескінченно малими одного
порядку в околі точки
називаються нескінченно малими одного
порядку в околі точки![]() .
.
Якщо
 ,
де
,
де![]() ,
,![]() додатне
число, то функція
додатне
число, то функція![]() називається нескінченно малою порядку
називається нескінченно малою порядку![]() відносно нескінченно малої функції
відносно нескінченно малої функції![]() .
.
Якщо
 ,
то нескінченно малі функції
,
то нескінченно малі функції![]() і
і![]() називаються непорівнянними в околі
точки
називаються непорівнянними в околі
точки![]() .
.
Якщо
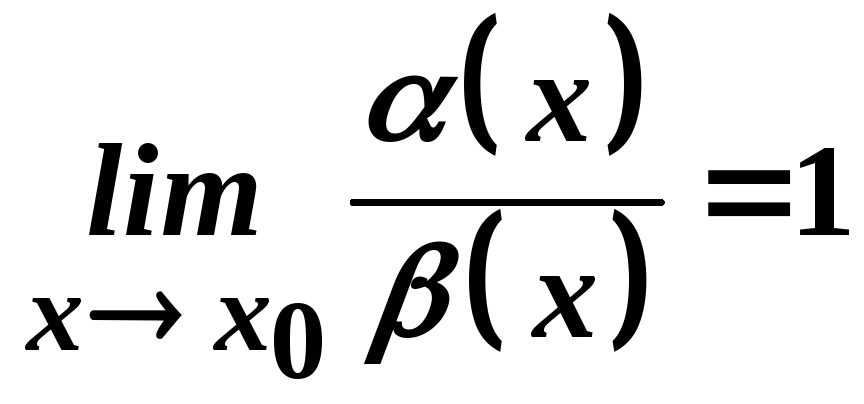 ,
то функції
,
то функції![]() і
і![]() називаються еквівалентними нескінченно
малими в околі точки
називаються еквівалентними нескінченно
малими в околі точки![]() .
У цьому випадку пишуть
.
У цьому випадку пишуть![]() .
.
Теорема.
Якщо
![]() при
при![]() й існує границя
й існує границя ,
то існує границя
,
то існує границя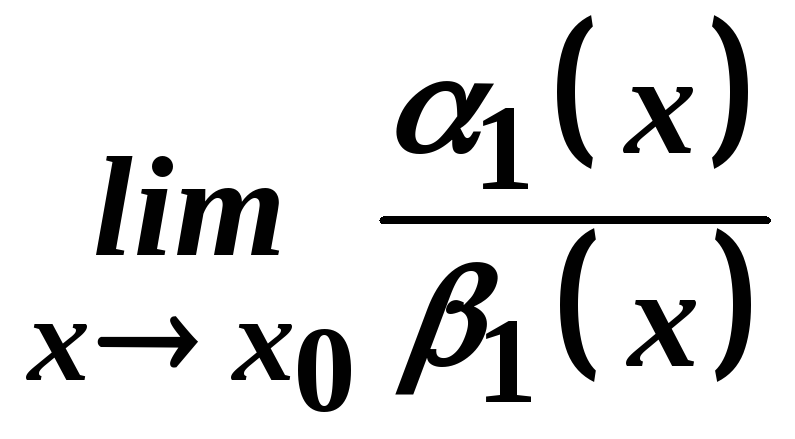 ,
причому
,
причому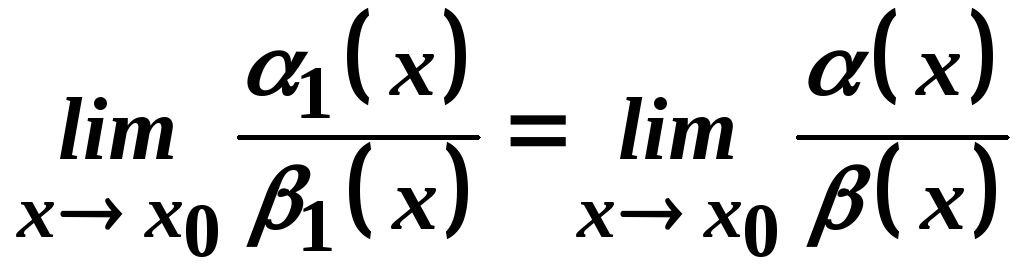 .
.
Доведення.
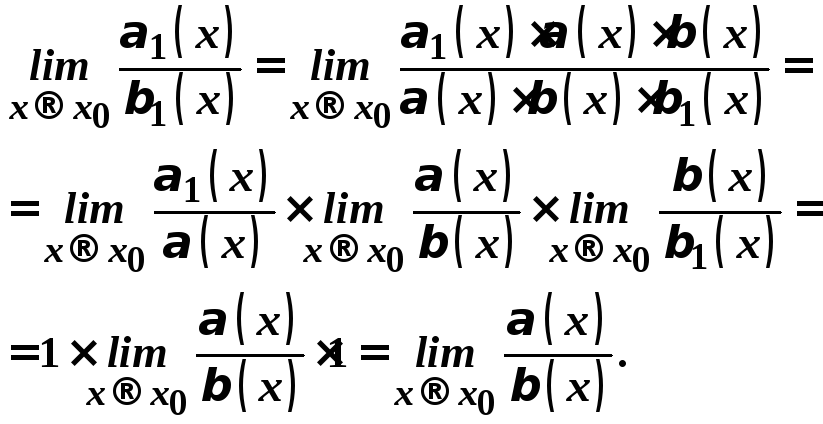
Наведена теорема дає можливість у багатьох випадках спрощувати знаходження границь.
Приклад.
При
![]() маємо
маємо![]() отже,
отже,
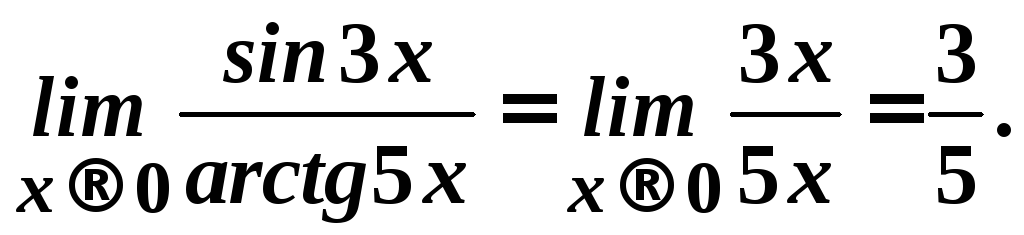
Теорема.
Для того, щоб функції
![]() і
і![]() були еквівалентними нескінченно малими
в околі точки
були еквівалентними нескінченно малими
в околі точки![]() ,
необхідно й достатньо, щоб їх різниця
,
необхідно й достатньо, щоб їх різниця![]() була в околі точки
була в околі точки![]() нескінченно малою вищого порядку по
відношенню до кожної з функцій
нескінченно малою вищого порядку по
відношенню до кожної з функцій![]() та
та![]() .
.
Доведення.
Нехай
![]() в околі точки
в околі точки![]() .
Тоді
.
Тоді

Отже, необхідність доведено. Доведемо достатність.
Нехай
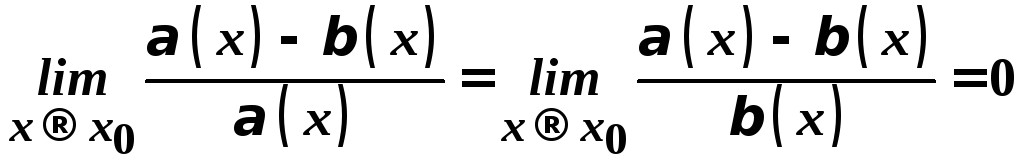 .
.
Звідси маємо
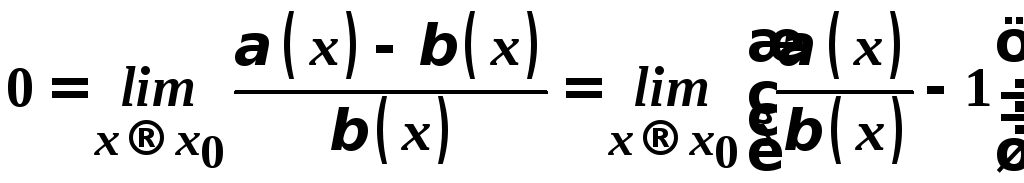 .
.
Таким
чином,
 ,
тобто в околі точки
,
тобто в околі точки![]()
![]() .
.
Тема 4. Неперервні та рівномірно неперервні функції
ЛЕКЦІЯ 12
Неперервність функції в точці.
Операції над неперервними функціями.
Класифікація точок розриву функції.
1. Неперервність функції в точці
Нехай
функція
![]() визначена в деякому околі
точки
визначена в деякому околі
точки
![]() .
.
Функція
![]() називається неперервною в точці
називається неперервною в точці
![]() ,
якщо
,
якщо
![]() .
.
Наведемо означення неперервності функції, які ґрунтуються на означеннях границі функції за Гейне і за Коші.
Функція
![]() називається неперервною в точці
називається неперервною в точці![]() ,
якщо для
будь-якої послідовності
,
якщо для
будь-якої послідовності
![]() відповідна послідовність
відповідна послідовність
![]() значень збігається до
значень збігається до
![]() .
.
Функція
![]() називається неперервною в точці
називається неперервною в точці
![]() ,
якщо
для
довільного числа
,
якщо
для
довільного числа
![]() існує число
існує число![]() таке, що для всіх
таке, що для всіх![]() ,
які задовольняють умову
,
які задовольняють умову![]() ,
виконується нерівність
,
виконується нерівність![]() .
.
Наведені означення рівносильні.
Функція
![]() називається неперервною в точці
називається неперервною в точці
![]() справа (зліва), якщо
справа (зліва), якщо
 .
.
Отже,
функція
![]() неперервна в точці
неперервна в точці
![]() ,
якщо вона неперервна в цій точці як
справа, так і зліва.
,
якщо вона неперервна в цій точці як
справа, так і зліва.
Покажемо,
що неперервна функція характеризується
тим, що нескінченно малому приростові
аргументу
![]() відповідає нескінченно малий приріст
функції
відповідає нескінченно малий приріст
функції![]() .
.
Дійсно,
умову
![]() можна записати як
можна записати як![]() .
Тоді
.
Тоді
![]() .
.
Отже,
можна дати наступне означення неперервності
функції в точці
![]() .
Функція
.
Функція
![]() називається неперервною в точці
називається неперервною в точці
![]() ,
якщо нескінченно малому приростові
аргументу в цій точці відповідає
нескінченно малий приріст функції.
,
якщо нескінченно малому приростові
аргументу в цій точці відповідає
нескінченно малий приріст функції.
Уведене
поняття неперервності функції є локальною
(місцевою) властивістю. Якщо функція
![]() неперервна
в кожній точці інтервалу
неперервна
в кожній точці інтервалу
![]() ,
то говорять, що вона неперервна на
інтервалі
,
то говорять, що вона неперервна на
інтервалі![]() .
Якщо при цьому в точці
.
Якщо при цьому в точці![]() функція неперервна справа, а в точці
функція неперервна справа, а в точці![]() –
неперервна зліва, то говорять, що функція
–
неперервна зліва, то говорять, що функція
![]() неперервна
на відрізку
неперервна
на відрізку
![]() .
.
Зауважимо,
що термін неперервної кривої походить
із поняття неперервної функції. Графіком
неперервної на
![]() функції є неперервна крива ("суцільна
крива").
функції є неперервна крива ("суцільна
крива").
2. Операції над неперервними функціями
Теорема.
Якщо функції
![]() неперервні в точці
неперервні в точці![]() ,
то функції
,
то функції у точці
у точці![]() також неперервні.
також неперервні.
Доведення цієї теореми безпосередньо випливає з означення неперервності функції в точці та властивостей границь.
Теорема
(про неперервність складеної функції).
Якщо функція
![]() неперервна в точці
неперервна в точці
![]() ,
а функція
,
а функція
![]() неперервна в точці
неперервна в точці
![]() ,
причому
,
причому![]() ,
то складена функція
,
то складена функція![]() неперервна, як функція від
неперервна, як функція від![]() ,
у точці
,
у точці![]() .
.
Доведення.
Нехай задано довільне число
![]() .
Тоді за неперервністю функції
.
Тоді за неперервністю функції
![]() у точці
у точці
![]() знайдеться число
знайдеться число![]() таке, що
таке, що![]() для всіх
для всіх![]() ,
які задовольняють умову
,
які задовольняють умову![]() .
.
Для
числа
![]() за неперервністю функції
за неперервністю функції![]() у точці
у точці![]() знайдеться число
знайдеться число![]() таке, що
таке, що![]() для всіх
для всіх![]() ,
які задовольняють умову
,
які задовольняють умову![]() .
.
Отже,
для довільного числа
![]() знайдеться число
знайдеться число![]() таке, що з умови
таке, що з умови![]() випливає нерівність
випливає нерівність![]() ,
а це означає, що функція
,
а це означає, що функція![]() неперервна в точці
неперервна в точці![]() .
.
Можна довести, що всі елементарні функції в області їх визначення неперервні.
Звернемо
увагу на те, що з означення неперервності
функції
![]() у точці
у точці
![]() випливає
випливає
 .
.
Наведемо приклади деяких важливих границь, обчислення яких спирається на неперервність елементарних функцій.
 .
.
Доведення.
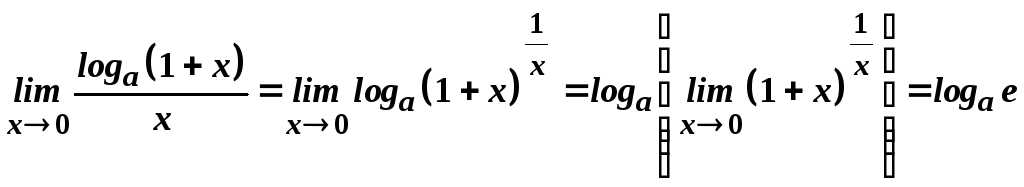 .
.
Якщо
![]() ,
то маємо:
,
то маємо: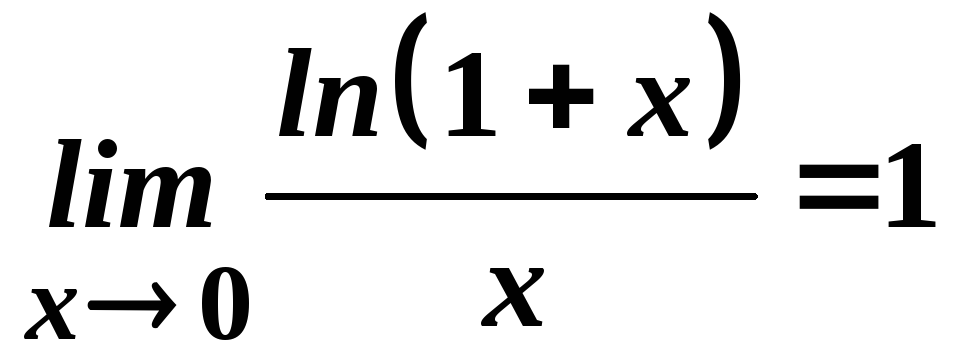 ,
тобто при
,
тобто при![]() виконується
виконується![]() .
.
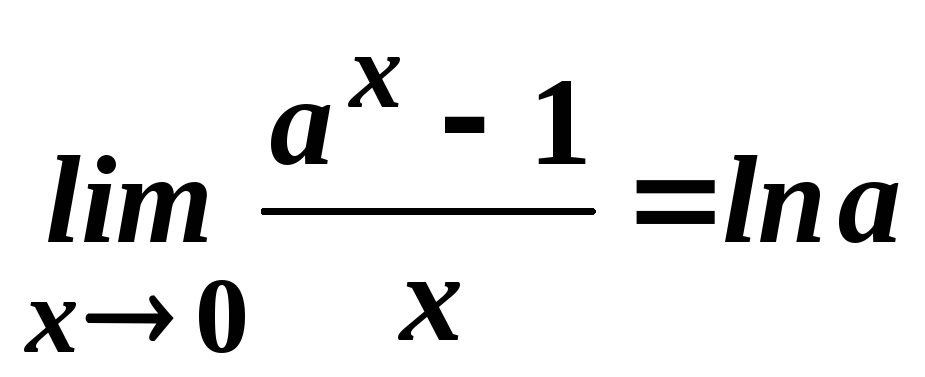 .
.
Доведення.
Покладемо
![]() .
Тоді
.
Тоді![]() .
Якщо
.
Якщо![]() ,
то
,
то![]() і
і![]() .
.
 .
.
Якщо
![]() ,
то маємо:
,
то маємо: ,
тобто при
,
тобто при![]() справедливо
справедливо![]() .
.
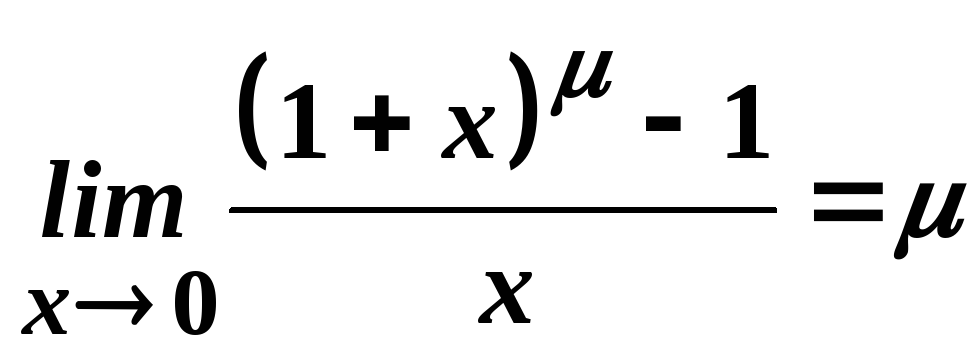 .
.
Доведення.
Покладемо
![]() .
Якщо
.
Якщо![]() ,
то
,
то![]() і
і![]() .
.
Далі
![]()
![]() .
Звідси маємо:
.
Звідси маємо: .
Тоді
.
Тоді

Розглянемо
степенево-показниковий вираз
![]() .
Нехай
.
Нехай
![]() .
Запишемо
.
Запишемо
![]() .
.
Оскільки
 ,
то
,
то![]() .
Звідси маємо
.
Звідси маємо
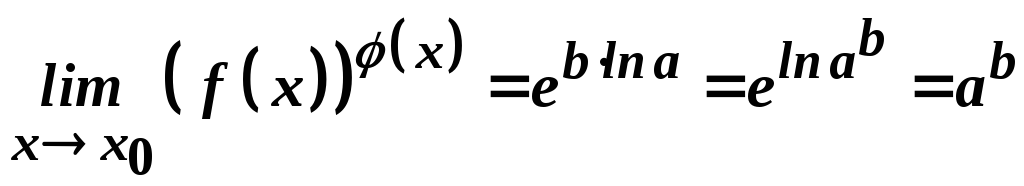 .
.
Зазначимо,
що вирази
![]() є не визначеними. Для знаходження
відповіді на питання, що є границею
виразу
є не визначеними. Для знаходження
відповіді на питання, що є границею
виразу![]() ,
у цих випадках недостатньо знати лише
границі функцій
,
у цих випадках недостатньо знати лише
границі функцій![]() ,
потрібно знати закон, за яким вони
прямують до своїх границь.
,
потрібно знати закон, за яким вони
прямують до своїх границь.
3. Класифікація точок розриву функції.
Точка
![]() називається точкою розриву функції
називається точкою розриву функції![]() ,
якщо функція
,
якщо функція![]() у точці
у точці![]() не є неперервною.
не є неперервною.
Точки розриву класифікують наступним чином.
Розриви
першого роду.
Якщо в точці
![]() функція
функція
![]() має скінченну ліву й скінченну праву
границю і вони рівні між собою, тобто
має скінченну ліву й скінченну праву
границю і вони рівні між собою, тобто
![]() ,
,
але
відмінні від значення функції
![]() в точці
в точці![]() або значення
або значення![]() не існує, то точка
не існує, то точка![]() називається точкою усувного розриву
функції
називається точкою усувного розриву
функції![]() .
.
Якщо в точці
![]() функція
функція![]() має скінченну границю справа і скінченну
границю зліва й
має скінченну границю справа і скінченну
границю зліва й![]() ,
то точка
,
то точка![]() називається точкою розриву функції
називається точкою розриву функції![]() із скінченним стрибком.
із скінченним стрибком.
Розриви
другого роду.
Точка
![]() називається точкою розриву другого
роду функції
називається точкою розриву другого
роду функції
![]() ,
якщо в цій точці функція
,
якщо в цій точці функція
![]() не має принаймні однієї з односторонніх
границь або хоча б одна з односторонніх
границь є нескінченною.
не має принаймні однієї з односторонніх
границь або хоча б одна з односторонніх
границь є нескінченною.
Кусково-неперервні
функції.Функція![]() називається кусково-неперервною на
відрізку
називається кусково-неперервною на
відрізку![]() ,
якщо вона неперервна в усіх внутрішніх
точках
,
якщо вона неперервна в усіх внутрішніх
точках![]() ,
за винятком, можливо, скінченного числа
точок, у яких має розрив 1-го роду і , крім
того, має односторонні границі в точках
,
за винятком, можливо, скінченного числа
точок, у яких має розрив 1-го роду і , крім
того, має односторонні границі в точках![]() та
та![]() .
.
