
- •Тема 1. Вступ. Дійсні числа
- •1. Вступ
- •2. Елементи теорії множин
- •1. Поняття відображення або функції
- •2. Потужність множин
- •3. Зчисленні множини
- •4. Математична індукція
- •1. Дійсні числа
- •1. Аксіоми додавання і множення
- •2. Аксіоми порівняння дійсних чисел
- •2. Деякі властивості дійсних чисел
- •Із означення множини дійсних чисел випливає, що ця множина впорядкована.
- •1. Поняття ізоморфізму
- •2. Інтерпретація множини дійсних чисел
- •3. Найбільш вживані числові множини
- •4. Межі числових множин
- •5. Абсолютна величина числа
- •Абсолютна величина числа позначається символом.
- •Тема 2. Числові послідовності
- •1. Означення числової послідовності
- •1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…,
- •2. Арифметичні дії над числовими послідовностями Нехай задано послідовності і.
- •2. Обмежені і необмежені числові послідовності
- •4. Нескінченно малі і нескінченно великі послідовності.
- •5. Основні властивості нескінченно малих послідовностей
- •1. Збіжні послідовності
- •2. Властивості збіжних послідовностей
- •3. Невизначені вирази.
- •1. Граничний перехід у нерівностях
- •2. Монотонні послідовності
- •3. Число е
- •4. Теорема про вкладені відрізки.
- •1. Теорема про вкладені відрізки.
- •3. Теорема Больцано-Вейєрштрасса
- •4. Критерій Коші збіжності числової послідовності.
- •1. Поняття метричного простору
- •2. Повні метричні простори.
- •3. Доповнення простору.
- •Тема 3. Границя функції однієї змінної
- •1. Границя функції. Означення границі функції за Гейне й за Коші.
- •2. Односторонні границі
- •3. Границя функції на нескінченності
- •4.Теореми про границі функцій
- •1. Визначні границі
- •2. Нескінченно малі й нескінченно великі функції
- •3. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
- •Тема 4. Неперервні та рівномірно неперервні функції
- •1. Неперервність функції в точці
- •2. Операції над неперервними функціями
1. Поняття метричного простору
Означення метричного простору. Багато фундаментальних фактів математичного аналізу не пов'язані з алгебраїчною природою дійсних чисел, а спираються лише на поняття відстані.
Узагальненням уявлень про дійсні числа як про множину, в якій уведено відстань між елементами, є поняття метричного простору.
Метричним
простором називається пара
![]() ,
що складається з деякої множини
,
що складається з деякої множини![]() елементів (точок) і відстані
елементів (точок) і відстані![]() – однозначної, невід'ємної функції,
визначеної для будь-якої пари
– однозначної, невід'ємної функції,
визначеної для будь-якої пари![]() ,
яка задовольняє наступні аксіоми:
,
яка задовольняє наступні аксіоми:
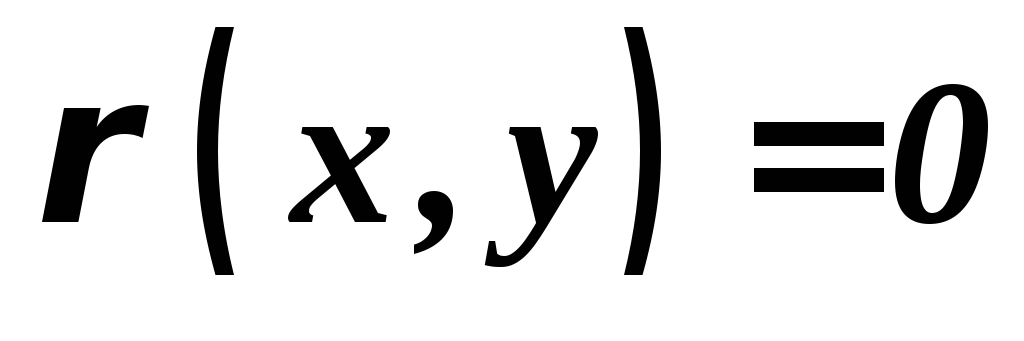 тоді
і тільки тоді, коли
тоді
і тільки тоді, коли
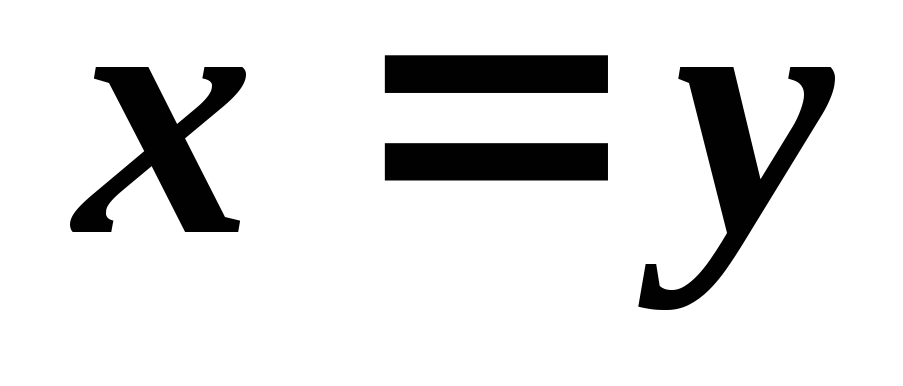 ;
; (аксіома
симетрії);
(аксіома
симетрії);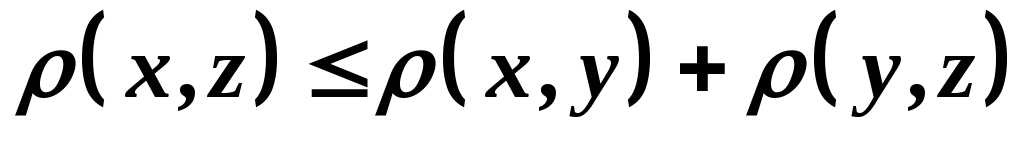 (аксіома
трикутника).
(аксіома
трикутника).
Сам
метричний простір, як правило, позначається
![]() .
.
Множина дійсних чисел із відстанню
![]()
утворює
метричний простір, що позначається
![]() .
.
Виконання аксіом метричного простору для введеної таким чином відстані випливає із властивостей абсолютної величини дійсного числа.
Відкритою
кулею
![]() у метричному просторі
у метричному просторі![]() називається сукупність точок
називається сукупність точок![]() ,
які задовольняють умову
,
які задовольняють умову
![]() .
.
Відкрита
куля радіуса
![]() з центром
з центром![]() називається
називається![]() -околом
точки
-околом
точки![]() і позначається
і позначається![]() .
.
У
просторі
![]() відкритою кулею з центром
відкритою кулею з центром![]() є множина точок
є множина точок![]() ,
для яких виконується нерівність
,
для яких виконується нерівність
![]() ,
,
а
![]() − околом точки
− околом точки![]() є множина точок
є множина точок![]() ,
для яких
,
для яких
![]() .
.
Точка
![]() називається точкою дотику множини
називається точкою дотику множини
![]() ,
якщо будь-який її окіл містить хоча б
одну точку з
,
якщо будь-який її окіл містить хоча б
одну точку з![]() .
Сукупність усіх точок дотику множини
.
Сукупність усіх точок дотику множини![]() позначається
позначається![]() і називається замиканням цієї множини.
і називається замиканням цієї множини.
Точка
![]() називається граничною точкою множини
називається граничною точкою множини![]() ,
якщо будь-який її окіл містить нескінченно
багато точок із
,
якщо будь-який її окіл містить нескінченно
багато точок із![]() .
.
Гранична
точка може належати, а може і не належати
![]() .
.
Точка
![]() називається ізольованою точкою множини
називається ізольованою точкою множини![]() ,
якщо вона належить
,
якщо вона належить![]() і існує такий
і існує такий![]() -окіл
точки
-окіл
точки![]() ,
у якому немає точок із
,
у якому немає точок із![]() ,
за винятком самої точки
,
за винятком самої точки![]() .
.
Усяка
точка дотику множини
![]() є або гранична, або ізольована точка
цієї множини.
є або гранична, або ізольована точка
цієї множини.
Нехай
![]() –
послідовність точок у метричному
просторі
–
послідовність точок у метричному
просторі
![]() .
Говорять, що ця послідовність збігається
в точці
.
Говорять, що ця послідовність збігається
в точці![]() ,
якщо
,
якщо![]() таке,
що
таке,
що
![]()
![]() .
.
Інакше
це означення можна сформулювати так:
послідовність
![]() збігається до
збігається до![]() ,
якщо
,
якщо![]() .
.
Теорема.
Щоб точка
![]() була точкою дотику множини
була точкою дотику множини
![]() ,
необхідно і достатньо, щоб існувала
послідовність
,
необхідно і достатньо, щоб існувала
послідовність![]() точок із
точок із![]() ,
яка збігається до
,
яка збігається до![]() .
.
Нехай
![]() – дві
множини простору
– дві
множини простору
![]() .
Множина
.
Множина![]() називається щільною у
називається щільною у![]() ,
якщо
,
якщо![]() .
Зокрема, множина
.
Зокрема, множина![]() називається скрізь щільною
у просторі
називається скрізь щільною
у просторі
![]() ,
якщо
,
якщо![]() .
.
Наприклад, множина раціональних чисел скрізь щільна на числовій прямій.
Множина
![]() називається ніде не щільною, якщо вона
не щільна в жодній кулі, тобто в кожній
кулі
називається ніде не щільною, якщо вона
не щільна в жодній кулі, тобто в кожній
кулі![]() існує інша куля
існує інша куля![]() ,
яка не має з
,
яка не має з![]() жодної спільної точки.
жодної спільної точки.
Простори, в яких є злічена скрізь щільна множина, називаються сепарабельними.
Множина
![]() метричного простору
метричного простору![]() називається замкнутою, якщо
називається замкнутою, якщо![]() ,
тобто якщо вона містить усі свої граничні
точки.
,
тобто якщо вона містить усі свої граничні
точки.
Відрізок
![]() числової прямої є замкнутою множиною.
числової прямої є замкнутою множиною.
Теорема. Переріз будь-якого скінченного числа замкнутих множин є замкнутою множиною. Сума будь-якого скінченного числа замкнутих множин є замкнутою множиною.
Точка
![]() називається внутрішньою точкою множини
називається внутрішньою точкою множини![]() ,
якщо існує окіл
,
якщо існує окіл![]() цієї точки, який цілком міститься в
цієї точки, який цілком міститься в![]() .
.
Множина, всі точки якої − внутрішні, називається відкритою.
Інтервал
![]() числової прямої
числової прямої![]() є відкритою множиною.
є відкритою множиною.
Теорема.
Щоб множина
![]() була відкрита, необхідно і достатньо,
щоб її доповнення
була відкрита, необхідно і достатньо,
щоб її доповнення![]() до всього простору
до всього простору![]() було замкнутим.
було замкнутим.
Теорема. Об'єднання (скінченного або нескінченного) числа відкритих множин є відкритою множиною. Переріз (скінченного або нескінченного) числа відкритих множин є відкритою множиною.
Теорема 1.5. Усяка відкрита множина на числовій прямій є сумою (об'єднанням) скінченного або зчисленного числа інтервалів, які попарно не перетинаються (не мають спільних елементів).
