4. Математична індукція

Математична індукція це метод доведення математичних тверджень, який полягає у наступному: твердження, яке залежить від натурального параметра, вважається доведеним, якщо доведеноііз припущення, що справедливе, доведено справедливість.

Доведення твердження називається першим кроком індукції (базисом індукції), а доведенняза припущення справедливостіназивається індуктивним переходом. При цьомуназивається параметром індукції, а припущенняпри доведенніназивається індуктивним припущенням.

Нехай – зчисленна множина і для n N

є множина впорядкованих n-членних ланцюгів. Тоді за твердженням 4 і методом (принципом) математичної індукціїє зчисленною множиною.

ЛЕКЦІЯ 3

1. Дійсні числа.

2. Деякі властивості дійсних чисел.

1. Дійсні числа

Уведемо аксіоматичне означення дійсних чисел. Із шкільного курсу математики відомо, що множина дійсних чисел складається із множини раціональних та ірраціональних чисел. Раціональним називається число, яке можна подати у вигляді звичайного дробу , де p, q −цілі числа, причому. Ірраціональним називається число, яке не є раціональним. Будь-яке раціональне число є або цілим, або скінченним чи нескінченним періодичним десятковим дробом. Ірраціональні числа – це нескінченні періодичні десяткові дроби. Виявлення ірраціональних чисел пов'язане з установленням у школі Піфагора (570-496 р. до н. е.) несумірності діагоналі квадрата і його сторони, тобто з установленням того факту, що довжина діагоналі квадрата не може бути виражена раціональним числом, якщо в значенні одиниці вимірювання взяти довжину сторони квадрата.

Ми дамо аксіоматичне означення множини дійсних чисел.

Множиною дійсних чисел називається множина елементів, для яких виконуються наступні аксіоми.

1. Аксіоми додавання і множення

Для будь-якої пари тадійсних чисел однозначно виражене число, яке називається їх сумою.

Для будь-якої пари ідійсних чисел однозначно виражене число , яке називається їх добутком.

Для будь-яких дійсних чисел a, b, c виконуються наступні аксіоми:

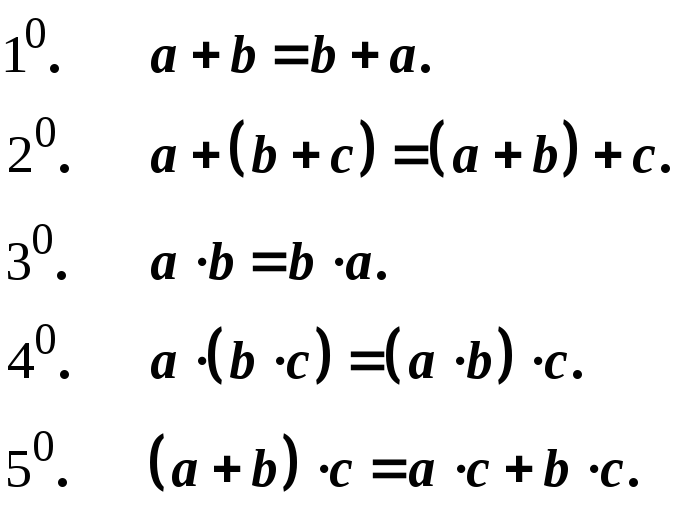
Існує єдине число 0, таке, щодля будь-якого числа.

Для будь-якого числаіснує таке число, що(числоназивається протилежним числу).

Існує єдине число 1, таке, що для будь-якого числа .

Для будь-якого числа існує таке число , що ; число позначається також символом і називається оберненим до.

2. Аксіоми порівняння дійсних чисел

Для будь-яких дійсних чисел a, b установлене одне із співвідношень:

Відношення "=" має властивість: якщо і, то.

Для будь-яких дійсних чисел a, b, c виконуються наступні аксіоми:

Якщоі, то.

Якщо, то.

Якщоі, то.

Зауваження.Замістьпишуть

3. Аксіома неперервності дійсних чисел

Нехайідві множини, які складаються із дійсних чисел. Тоді, якщо, виконується нерівність, то існує принаймні одне дійсне число, для якого виконується нерівність.

Зауваження.У множині лише раціональних чисел аксіома неперервності не виконується. Дійсно, нехайскладається із множини раціональних чисел, таких, що, а− із множини раціональних чисел. Тодівиконується нерівність. Проте не існує раціонального числа, такого, щобвиконувалася б нерівність. Таким числом могло бути лише число, а воно, як відомо, ірраціональне.