
- •Пределы функций. Дифференциальное исчисление
- •Донецк 2006
- •Ббк 22.161я73
- •Содержание
- •Введение
- •I. Теория пределов Основные понятия
- •Предел функции
- •1.2.1. Основные понятия
- •1.2.2. Основные свойства о пределах функции
- •1.2.3. Раскрытие неопределенностей
- •1.3. Непрерывность функции
- •2.1. Производная функции
- •2.2. Таблица производных
- •2.3. Основные правила дифференцирования
- •2.4. Дифференциал функции
- •2.5. Производные и дифференциалы высших порядков
- •2.6. Исследование функций и построение графиков
- •2.6.1. Промежутки монотонности функции
- •2.6.2. Экстремум функции
- •2.6.3. Наименьшее и наибольшее значение функции
- •2.6.4. Выпуклость и вогнутость функции. Точки перегиба
- •2.6.5. Асимптоты графика функции
- •2.6.6. Исследование функции и построение графика
- •3. Дифференциальное исчисление Функции нескольких переменных
- •3.1. Основные понятия
- •3.2. Частные производные
- •3.3. Полный дифференциал
- •3.4. Экстремум функции нескольких переменных
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Литература
2.2. Таблица производных
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.3. Основные правила дифференцирования
Производная алгебраической суммы функций равна алгебраической сумме производных этих функций, т.е.
![]() .
.
Производная произведения равна сумме произведений производной одного из множителей на остальные, т.е.
![]() .
.
Производная частного:
![]() .
.
Постоянный множитель можно выносить за знак производной, т.е.
![]() .
.
Пусть
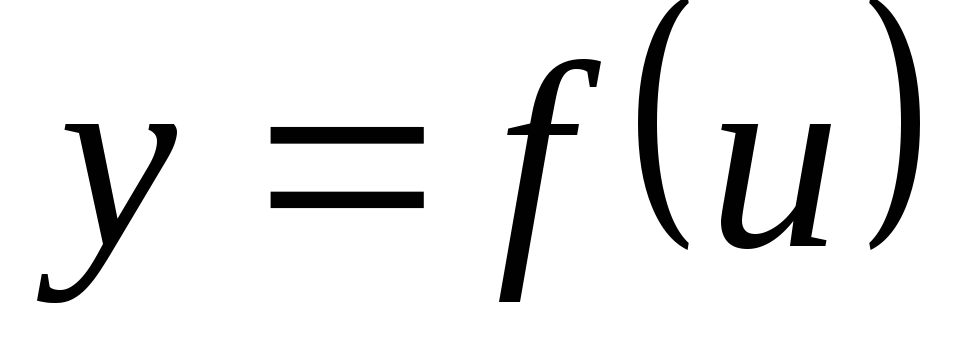 ,
а
,
а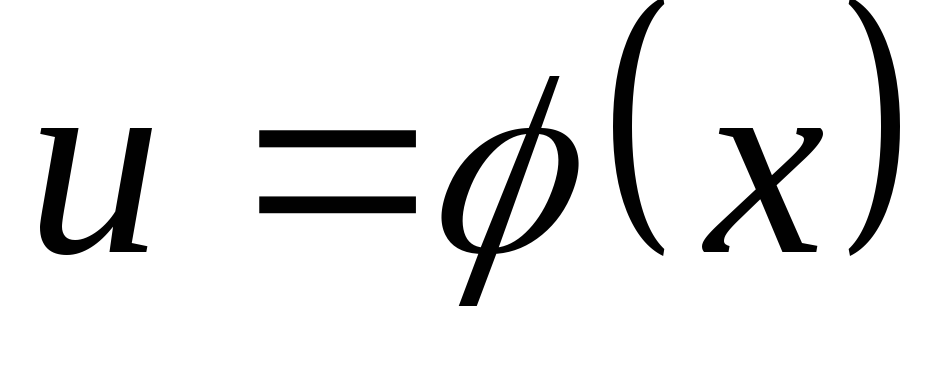 ,
т.о.
,
т.о. .
Тогда производная сложной функции по
независимой переменной равна произведению
производной этой функции по промежуточной
переменной на производную промежуточной
переменной по независимой переменной,
т.е.
.
Тогда производная сложной функции по
независимой переменной равна произведению
производной этой функции по промежуточной
переменной на производную промежуточной
переменной по независимой переменной,
т.е.
![]() .
.
Пример
2.1. Найти
производную функции
![]()
Решение.
Полагая
![]() ,
,![]() ;
;![]() ;
получим
;
получим
![]()
При достаточном количестве упражнений необходимость в записи промежуточных переменных отпадает.
Если
функция задана неявно, т.е. уравнением,
не разрешенным относительно
![]() (
(![]() ),
то для нахождения производной
),
то для нахождения производной![]() надо продифференцировать по
надо продифференцировать по![]() обе части этого уравнения, учитывая,
что
обе части этого уравнения, учитывая,
что![]() есть функция от
есть функция от![]() ,
и затем разрешить полученное уравнение
относительно
,
и затем разрешить полученное уравнение
относительно![]() .
.
Пример
2.2. Найти
производную функции
![]() .
.
Решение.
Дифференцируем
по
![]() обе части данного равенства и считаем
обе части данного равенства и считаем![]() функцией от
функцией от![]() ,
находим
,
находим
![]() .
.
Из
полученного равенства находим
![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
Логарифмическая
производная функции
![]() есть производная от логарифма данной
функции:
есть производная от логарифма данной
функции:
![]() .
.
Вычисление логарифмической производной называется логарифмическим дифференцированием.
Логарифмическое
дифференцирование применяется при
вычислении производной степенно-показательной
функции, т.е. функции вида
![]() ,
а также при нахождении производной
произведения нескольких функций или
производной дроби.
,
а также при нахождении производной
произведения нескольких функций или
производной дроби.
Пример
2.3. Найти
производную функции
![]() .
.
Решение.
Функция
![]() – степенно-показательная.
– степенно-показательная.
Прежде чем дифференцировать, прологарифмируем данную функцию:
![]() ;
;
![]() .
.
Дифференцируем как неявно заданную функцию:
![]()
Из
полученного равенства выразим
![]() :
:
![]()
Вместо
![]() подставим
подставим![]() :
:
![]() .
.
Пример
2.4. Найти
производную функции
![]() .
.
Решение. Прологарифмируем данную функцию
![]() ;
;
![]() .
.
Дифференцируем:
![]()
![]()
![]() .
.
2.4. Дифференциал функции
Дифференциалом
![]() функции
функции![]() называется главная линейная относительно
называется главная линейная относительно![]() часть ее приращения.
часть ее приращения.
Дифференциал
![]() независимой переменной
независимой переменной![]() равен ее приращению:
равен ее приращению:
![]() .
(2.4.1)
.
(2.4.1)
Дифференциал
любой дифференцируемой функции
![]() равен произведению ее производной на
дифференциал независимой переменной:
равен произведению ее производной на
дифференциал независимой переменной:
![]() .
(2.4.2)
.
(2.4.2)
Основные правила нахождения дифференциалов аналогичны основным правилам вычисления производных:
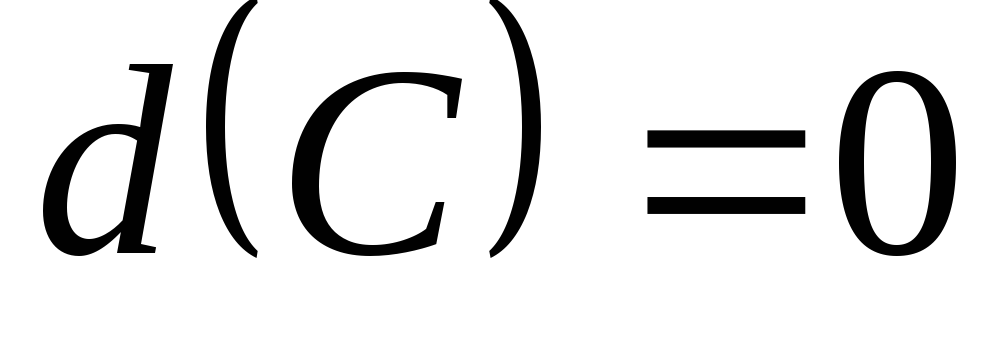 ;
; ;
; ;
; ;
;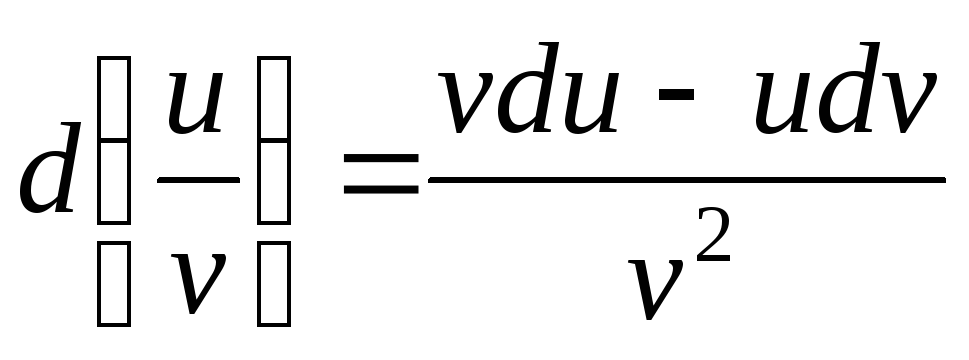 .
.
Если
![]() достаточно мало, то имеет место
приближенное равенство:
достаточно мало, то имеет место
приближенное равенство:
![]() ,
,
которое используется при применении дифференциала к приближенным вычислениям.
![]() (2.4.3)
(2.4.3)
Пример
2.5. Вычислить
приближенно
![]() .
.
Решение.
Рассмотрим функцию
![]() и положим
и положим![]() ,
,![]() .
.
Воспользовавшись
формулой (2.4.3), найдем
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Таким
образом,
![]() ,
т.е.
,
т.е.![]() .
.
