2.6.4. Выпуклость и вогнутость функции. Точки перегиба

Кривая называется выпуклой (вогнутой) в некотором промежутке, если она расположена ниже (выше) касательной, проведенной к кривой в любой точке этого промежутка. Выпуклость или вогнутость кривой характеризуется знаком второй производной, а именно, если в некотором промежутке, то кривая выпукла, если, то вогнута.

Точкой перегиба кривой называется такая ее точка, которая отделяет участок выпуклости от участка вогнутости.

Точками перегиба графика функции могут служить точки, находящиеся внутри области определения функции, в которых вторая производнаяобращается в нуль или терпит разрыв, и при переходе через которые вторая производнаяменяет знак.

Таким образом, получаем правило отыскания промежутков выпуклости и вогнутости и точек перегиба графика функции.

1. Найти вторую производную функции .

2. Найти точки, в которых вторая производная обращается в нуль или не существует.

3. Определить знак второй производной на каждом промежутке.

4. Найти точки перегиба.

Пример 2.13. Исследовать на выпуклость, вогнутость и точки перегиба график функции .

Решение. Область определения функции . Находим вторую производную, дифференцируя функцию дважды.

существует на всей оси и обращается в нуль в точках:

.

Определим знак второй производной на промежутках:

0 1

На интервале – функция выпукла, на интервале– вогнута. Точка с абсциссой– не является точкой перегиба, т.к. вторая производная не меняет знак при переходе через нее.

Точка с абсциссой – точка перегиба. Найдем значение функции в этой точке.

.

Таким образом, – точка перегиба.

2.6.5. Асимптоты графика функции

Прямая называется асимптотой кривой , если расстояние от точки, лежащей на кривой, до этой прямой стремится к нулю при удалении точкив бесконечность.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

Вертикальной асимптотой является прямая , проходящая через точку разрыва функции.

Уравнение наклонной асимптоты имеет вид:

, (2.6)

где ;.

Прямая являетсягоризонтальной асимптотой, если существует конечный предел функции при или(горизонтальная асимптота – частный случай наклонной асимптоты при).

Пример 2.14. Найти асимптоты кривой .

Решение. Кривая имеет вертикальную асимптоту (в точкефункция не существует). Найдем наклонные асимптоты.

;

.

Таким образом, – наклонная асимптота

2.6.6. Исследование функции и построение графика

Общее исследование функции и построение ее графика выполняется по следующей схеме:

1. Найти область определения.

2. Проверить, не является ли функция четной или нечетной, периодической.

3. Найти промежутки монотонности функции и ее экстремумы.

4. Найти промежутки выпуклости и вогнутости графика функции и его точки перегиба.

5. Найти асимптоты графика функции.

6. Построить по полученным результатам график функции.

Пример 2.15. Исследовать функцию и построить график.

Решение.

1. Область определения :;. Функция существует на интервалах:.

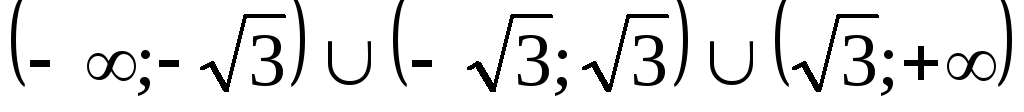2. –условие четности; – условие нечетности

, т.е. .

Функция нечетная, ее график симметричен относительно начала координат.

3. Находим первую производную

.

Найдем критические точки. Первую производную приравняем к нулю

.

Таким образом, это критические точки. На числовую ось нанесем критические точки и точки разрыва.

Определим промежутки возрастания и убывания, точки экстремума (по знаку первой производной)

0 3

Поскольку на интервалах, то функция на них убывает, посколькуна интервале, то функция возрастает на этом интервале.

–точка минимума, – точка максимума.

Найдем экстремум функции

–; –.

4. Находим вторую производную.

.

Найдем критические точки: .

Таким образом, – критическая точка.

Определим знак на промежутках

0

На интервалах – график функции вогнутый. На интервалах– выпуклый. Точка– точка перегиба.

5. и – вертикальные асимптоты (прямые, проходящие через точки разрыва).

Найдем наклонные: .

–наклонная асимптота.

6. Строим график функции (рис. 2.2.)

														4,5
							– 3												3
											-4,5

Рисунок 2.2 – График искомой функции