
- •Український державний хіміко-технологічний університет
- •2. Математична модель в системі управління
- •2.1. Головні поняття технічної кібернетики
- •2.2.1. Загальні характеристики інформації.
- •2.2.2. Інформаційні процеси
- •2.3.1. Загальні поняття та терміни
- •2.3.2. Графічне відображення оптимізації
- •Var de:text;
- •I,Imin,Imax,dI,р,рc,eps,u,u0 :real;
- •2: Writeln(de); writeln (de, k:3,' I-u-р-dI',I:6:2, u:6:2, р:6:2, dI:10:5);
- •3.3.Масообмінні процеси в системах промивання в гальванотехніці
- •3. Математичне моделювання технологічних процесів в електрохімічних апаратах
- •3.1. Масообмінні процеси в електрохімічних апаратах.
- •3.2 Електрохімічні апарати ідеального змішування
- •3.2.1. Загальна математична модель нестаціонарного масообміну в еха.
- •3.2.2. Математична модель нестаціонарних процесів в непроточних еха ідеального змішування
- •3.2.3. Алгоритми та програма числового моделювання масообміну в еха ідеального змішування.
- •1 Real I,ma,mb,j1,j2
- •2 Data aa,ab,ea,eb,eg,et,t,dt/0.7,0.98,2.18,1.49,0,0,0,0.1/
- •3 Data camin, cbmax, I , ca , cb , V , v0 , j1 , ca1 , cb1
- •23 If(ca.Le.Camin.Or.Cb.Ge.Cbmax) goto 3
- •3.3. Математична модель стаціонарних процесів в проточних еха ідеального змішування
- •1 Real I, j1,j2
- •3.4 Процеси в електрохімічних апаратах ідеального витискування.
- •Var Rom, pR,pO,kap,tok,u,Ut,co,cr,ir,V,h,er,eo,l,dx :real;
- •4. Нестаціонарний масообмін в приелектродному шарі
- •5.5. Моделювання розсіюючої здатності електроліту
- •5. Електричні поля в електрохімічних системах
- •5.1. Двовимірне електричне поле.
- •5.4. Приклади дії електричних полів в системах технічної електрохімії і способи управління полями.
- •6. Моделювання процесів в пористих системах
- •6.1. Об’єкти вивчення
- •6.2. Електричне поле в рідинному пе.
- •6.3. Стаціонарний процес в ріднному пористому електроді. Концентраційні поля.
- •6.4. Стаціонарні транспортні процеси в пористих сепараторах
- •7.Витоки струму в високовольтних електрохімічних пристроях
6.2. Електричне поле в рідинному пе.
На внутрішній поверхні пор здійснюються звичайний електрохімічний процес. Але до поверхні потрібно доставити реагент і відвести продукт, і механізмів транспорту три – конвекція (продавлювання розчину), дифузія і міграція (рух заряджених іонів в електричному полі. Це задача з одного боку більш складна, ніж ми розглядали досі. Але з другого боку, її можна дещо спростити, розглядаючи окремі механізми транспорту не разом (як вони діють насправді), а окремо. Крім того, задачу будемо розглядати як одновимірну, вважаючи пористе тіло як гомогенний і ізотропний матеріал, в якому всі параметри змінюються лише по одній координаті «х», тобто перпендикулярно поверхні електроду. Можна сказати, що це задача розрахунку одновимірних полів.
В цьому розділі ми розглянемо спрощену задачу лише про одне поле – електричне.
Електричну
модель пористого електрода товщиною
h
можна представити так. Розділимо умовно
електрод на N шарів (по рис. 6.2 N=4), кожний
товщиною х
= h/(N-1).
В кожному шapi можна розрахувати ефективний
опір електроліту
![]() та твердої фази rT,
урахувуючи коефіцієнт підвищення опору
в порах. Представимо кожну фазу ланцюгом
послідовно включених резисторів, rE
та rT.
Обидва ланцюги зв’язані в кожному шарі
через поляризаційний опір rП.
Поляризаційний опір окремого шару x
залежить від поляризаційного опору
одиниці істинної поверхні d/di
) і обернено пропорційний його питомій
внутрішній поверхні:
та твердої фази rT,
урахувуючи коефіцієнт підвищення опору
в порах. Представимо кожну фазу ланцюгом
послідовно включених резисторів, rE
та rT.
Обидва ланцюги зв’язані в кожному шарі
через поляризаційний опір rП.
Поляризаційний опір окремого шару x
залежить від поляризаційного опору
одиниці істинної поверхні d/di
) і обернено пропорційний його питомій
внутрішній поверхні:
![]() ,
(6.2)
,
(6.2)
З рис.6.2 видно, що локальні струми, які протікають через перший і останній шар, можна оцінити із приблизних співвідношень
![]() ,
,
![]() ,(6.3)
,(6.3)
де Е – поляризація, яка вимірюється на фронтальній поверхні електрода.
Із виразів (6.3) видно, що співвідношення між струмами і1 та і4, тобто залежить від співвідношення між трьома опорами одиничної ланки - rE , rT , rП.
Найчастіше
в пористих електродах, які виготовлені
з електропровідних матеріалів (метал,
графіт, сажа), опір
твердої фази на 4-5 порядків менший за
опір електроліту,
тому ним можна знехтувати. Якщо і
поляризаційний опір малий, тоді головним
фактором, від якого залежить розподіл
струму, буде омічний опір електроліту
в порах, rE>>(rT+
rП
0).
Тоді
![]() ,
тобто струм локалізується в порах
поблизу фронтальної поверхні електрода.
,
тобто струм локалізується в порах
поблизу фронтальної поверхні електрода.
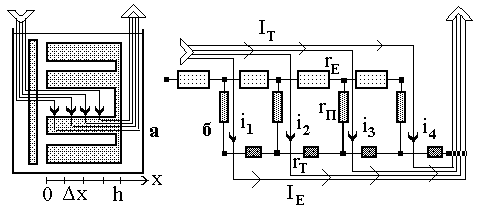
Рис.
6.2. Схема роботи рідинного пористого
електрода (а) і його електрична модель
(б). ІЕ
, ІТ
– інтегральний струм в електроліті і
твердій фазі, і1…і4
– локальні струми секцій.
Якщо поляризаційний опір значний, при умові rП >> (rT+ rE 0) із (6.3) одержимо
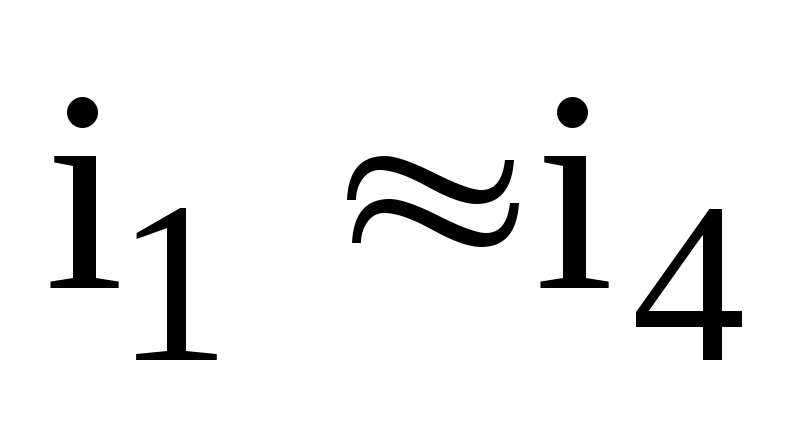 ,
тобто густина струму однакова по всій
глибині пор. (Корисно згадати, що така
ситуація відома в гальванотехніці: при
високому поляризаційному опорі катодного
процесу електроліти мають високу
розсіюючу здатність, яка і полягає в
рівномірному розподілу локальної
густини струму на поверхні геометрично
складних виробів).
,
тобто густина струму однакова по всій
глибині пор. (Корисно згадати, що така
ситуація відома в гальванотехніці: при
високому поляризаційному опорі катодного
процесу електроліти мають високу
розсіюючу здатність, яка і полягає в
рівномірному розподілу локальної
густини струму на поверхні геометрично
складних виробів).
Опір твердої фази найбільший , rT>>(rП+rE 0). В цьому випадку максимальний струм генерує останній шар №4, який розташований найближче до струмовідвода на тильній межі електрода:
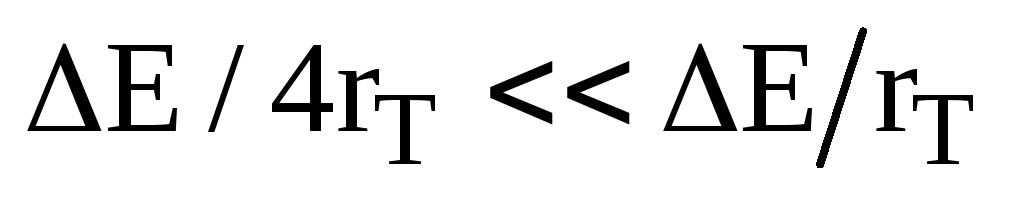 ,
, .
.
Таким чином можна зробити висновок: через дію електричного опору електроліту внутрішня поверхня пористого електроду працює нерівномірно, і електрохімічний процес проникає лише на деяку невелику глибину від фронтальної поверхні, яка межує з електролітом.
Аналітичні рішення задачі. Наведені орієнтовні оцінки густини струму в порах наглядні, але для кількісних оцінок непридатні. Точніші розрахунки можна виконати для спрощеної умови, коли основний фактор гальмування процесу - омічно-електролітний, rE+ rП >> (rT 0). Диференційне рівняння, яке описує розподіл поляризації в порах по координаті товщини х, має вигляд ( це є одновимірне рівняння Пуассона):
![]() ,
(6.4)
,
(6.4)
з граничними умовами
![]() ,
,
![]()
![]() ,
(6.5)
,
(6.5)
де і() - локальна поляризаційна характеристика внутрішньої поверхні, І–габаритна густина струму, Е –питомий опір електроліту .
Далі можна розглянути два часткових випадки, які мають місце в реальних умовах.
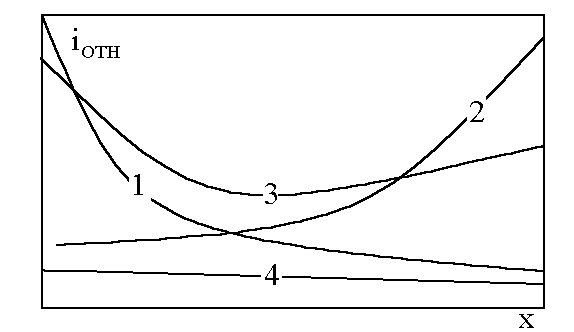
Рис.
6.3.
Якісний характер розподілу густини
струму в пористому електроді. rE
>>
(rT+
rП
0); rT
>>( rП
+ rE
0); (rE
rT)
>>
rП; rП
>> (rT+
rE
0).
Найпростіші і наглядні рішення відомі для невеликих поляризацій, коли поляризаційна характеристика має лінійну форму:
![]() ,
,
![]() ,
,![]() (6.6)
(6.6)
де rп - локальний поляризащйний опір, Омсм2, b- константа, io –локальна густина. струму обміну на одиницю внутрішньої поверхні, А/см2.
Рішення рівняння (6.5) дає таку функцію розподілу густини струму по глибині пористого електрода, А/см2:
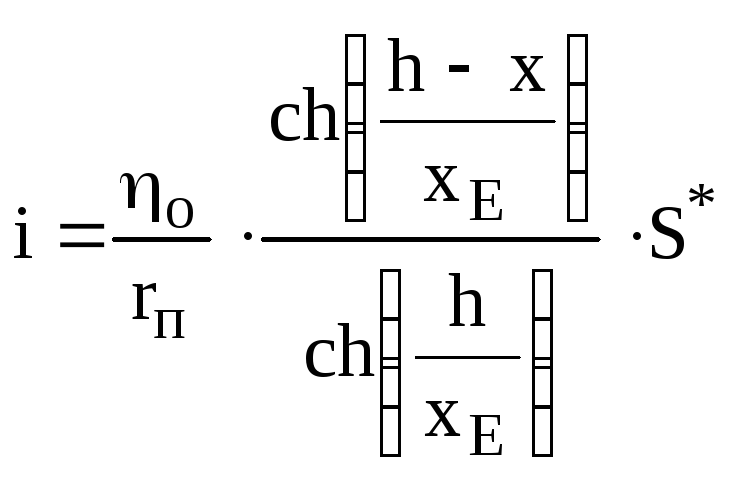 ,
,
![]() (6.7)
(6.7)
Параметр хЕ є характерним масштабним критерієм неоднорідності розподілу електрохімічного процесу по глибині пористого електрода. Його значення залежить від співвідношення між поляризаційним опором внутрішньої поверхні і омічним опором електроліту в порах.
Як видно з (6.7), при високих значеннях поляризаційного опору (rп/S*)>>E значення критерія хЕ перевищує товщину електрода, хЕ>>h, тому густина струму однакова по всій товщині (графік 4 на рис.6.3).
Навпаки, для умов роботи активних електродів з малим поляризаційним опором (rп/S*)<<E характерне таке відношення: хЕ<h. Воно означає, що електрохімічний процес локалізований тільки в поверхневому шарі товщиною ххЕ. На рисунку 6.2 таким умовам відповідає графік 1.
Інтегрування функції (6.7) дає залежність габаритної густини струму електрода, яка вимірюється безпосередньо, від його товщини:
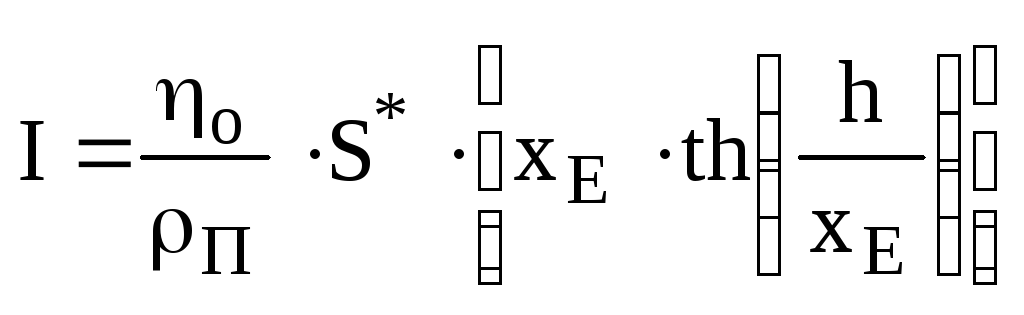 .
(6.8)
.
(6.8)
Максимальний (теоретичний) струм, який би генерував умовний електрод з рівнодоступною внутрішньою поверхнею, можна визначити згідно (6.8) як добуток
![]() .
(6.9)
.
(6.9)
Із порівняння (6.8) та (6.9) визначають важливу характеристику пористого електрода – ефективність, або ступінь використання внутрішньої поверхні пористого електрода
![]() .
(6.10)
.
(6.10)
На рис. 6.4 показана залежність критерію (лінія 3) від відносної товщини електрода h/xE. Для “тонких” електродів h<хЕ габаритний струм пропорційний товщині h, і ця залежність показана на рисунку прямою лінією 1. В той же час на “товстих” електродах (h/хЕ>4-6) габаритний струм майже не залежить від товщини, бо струмогенеруюча частина внутрішньої поверхні розташована на глибині х<(1-2)хЕ, і збільшення товщини непрацюючої частини дає лише негативні наслідки (лінія 2).
Рис.
6.4.
Залежність параметрів пористого
електроду від товщини. 1- теоретичне
значення габаритного струму, 2- фактичний
струм, 3- коефіцієнт ефективності
використання внутрішньої поверхні.

Числове інтегрування рівняння (6.4)
Математична модель. Ми розглянули найпростішу задачу з лінійною поляризаційною характеристикою =irП. Для реальних нелінійних поляризаційних характеристик (будь-яких) задачу можна вирішити числовими методами. Алгоритм аналогічний тому, яким вирішувались задачі двовимірних полів (ітераційний).
Замість (6.4) запишемо два аналогічних рівняння, які описують розподіл потенціалів електроліту U та твердої фази V по глибині х пористого електрода :
![]()
![]() ,
,
![]() , (6.11)
, (6.11)
де
Е
та Т
- ефективний питомий опір електроліту
та твердої фази (з урахуванням пористої
структури фаз), іV
=і·S*– локальне (на глибині “х”) значення
об’ємної
густини струму (А/см3).
Різниця потенціалів фаз (U-V)=f(x)
розглядається як поляризація
в рівнянні електрохімічної кінетики
![]() . Внутрішня питома поверхня електрода
S*
(см2/см3)
може
бути приблизно розрахована через
середній радіус частинок твердої фази
R :
. Внутрішня питома поверхня електрода
S*
(см2/см3)
може
бути приблизно розрахована через
середній радіус частинок твердої фази
R :
![]() .
(6.12)
.
(6.12)
Рівняння (6.11) запишемо в дискретній різницевій формі (6.13):
![]() ,
,
![]() ,
,
де = h/(N-1) -крок (dx) по координаті “х” електричної моделі електрода (рис.6.2) товщиною h з N вузлами..
Граничні умови: величини потенціалу електроліту на фронтальній поверхні електрода Ux=0, потенціалу твердої фази на тильній поверхні (струмовиводі) Vx=h,; нульові похідні потенціалу (тобто відсутність струму) в електроліті на тильній межі, і в твердій фазі на фронтальній межі :
Ux=0 = U0 ; Vx=h=0; dU/dxх= h =0; dV/dxx=0 =0. (6.14)
Кінетична
характеристика електрохімічного процесу
![]() може бути задана довільною функцією,
наприклад,
рівнянням
загальмованого розряду
може бути задана довільною функцією,
наприклад,
рівнянням
загальмованого розряду
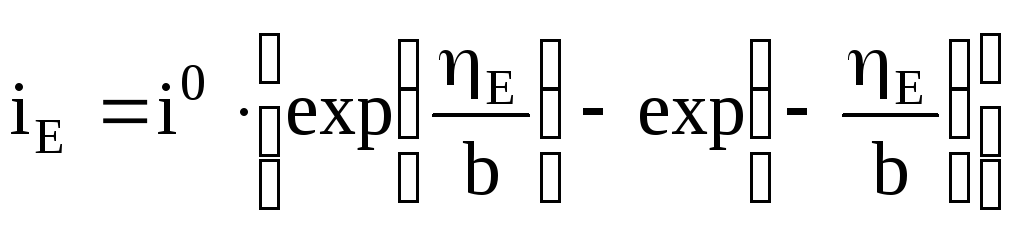 .
(6.15)
.
(6.15)
Алгоритм рішення аналогічний розглянутому в розділі 5. Всі розрахунки ведуться за умови постійного потенціалу або поляризації.
1. Для підготовки спочатку встановлюють відповідно до перших двох граничних умов (6.14) потенціали граничних вузлів. Для всіх інших вузлів встановлюють довільні значення U,V<U0 .
.
2. Далі виконується багаторазова ітераційна процедура, яка складається з таких елементів.
2.1. Перераховують за формулами (6.13) потенціали U,V для всіх внутрішніх вузлів з номерами 2….(N-1). При цьому на кожному кроці підраховують нові значення густини струму
2.2. Відповідно до другої пари умов в (6.14), де повинні бути нульові похідні потенціалів, встановлюють значення потенціалів крайніх вузлів:
UN =UN-1 ; V1 = V2 . (6.16)
2.3. Підраховують загальний (габаритний) струм електроду як суму локальних струмів всіх секцій х.
2.4. Перевіряють сходження ітерацій. Це можна виконати різними методами, наприклад, підраховуючи величину загального (габаритного) струму і порівнюючи значення на двох сусідніх кроках. Якщо ця різниця зменшиться до задовільного рівня помилки, ітераційний процес зупиняють.
Результатом розрахунку буде дискретна функція розподілу густини струму по глибині пористого електроду, а також його інтегральний струм.
