
EKh / конспект ММ / 6-Б-пористые
.doc6.3. Стаціонарний процес в ріднному пористому електроді. Концентраційні поля.
В попередньому пункті ми розглянули важливу, але спрощену чисто електричну задачу, ігноруючи явища, пов’язані з доставкою реагентів в пори, відведенням продуктів, і неминучістю виникнення через це концентраційної поляризації.
Реально процеси транспортування реагентів та продуктів електрохімічних реакцій в порах є паралельно діючим і важливим гальмівним фактором впливу на процеси в порах, а поляризація внутрішньої поверхні має значну концентраційну складову. Якісно структура розподілу поляризацій та потенціалів показана на рис.6.5 для випадку, коли опір твердої фази помітний і її потенціал, тобто повне омічне падіння напруги, також має деяке ненульове значення V0.
Потенціали в електроліті та в твердій фазі змінються по глибині так, як це відповідає схемі рис. 6.2, і їх розподіл по глибині „х” описують рівняння (6.11).
Рис.
6.5. Розподіл потенціалів та поляризацій
по глибині пористого електроду (якісно)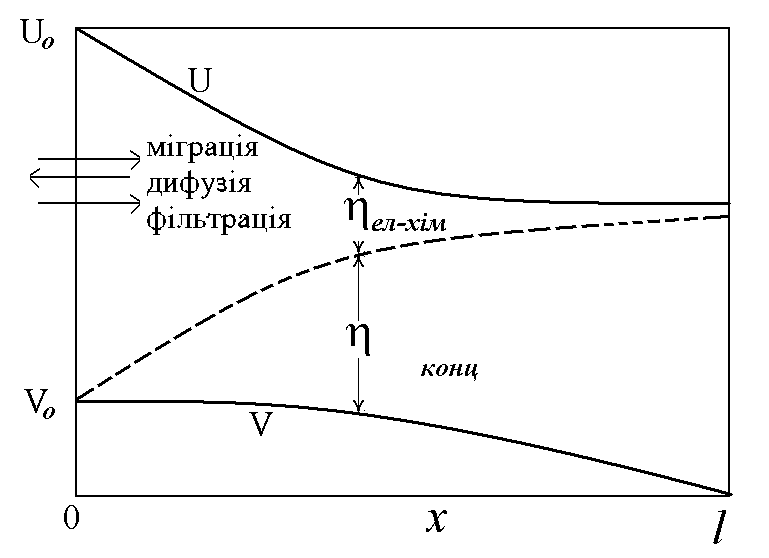
Для всіх компонентів електроліту (іони, нейтральні молекули) існує рівняння переносу, яке відображує рух частинок трьома незалежними механізмами: дифузією, фільтрацією через пори, міграцією в електричному полі:
![]() ,
(6.17)
,
(6.17)
де z–зарядове число частинки, v0- її рухомість, j- густина фільтраційного потоку см3/(см2 с) в напрямку товщини електроду „х”.
В залежності від напрямку фільтрації знак другого доданку може бути негативним (рух справа наліво, напроти напрямку осі „х”) або позитивним.
У міграційної складової сумарного потоку справжній знак третього доданка (тобто напрямок руху частинки) залежить від двох факторів: напрямку градієнта потенціалу в електроліті dU/dx і знака заряду „z” частинки. На рис. 6.5 знак dU/dx негативний. Тоді для катіона (+ z) загальний знак буде (-)·(-)·(+)=(+), тобто катіон буде рухатись зліва направо, в глибину пор. Інакше можна сказати, що пористий електрод (схема рис. 6.2) є катодом електролізера або анодом джерела струму ( в обох випадках це негативний полюс, електрод поляризується в негативному напрямку потенціалу, і тому до цього електроду рухаються позитивно заряджені катіони).
Рівняння
(6.17) є особливим інтегро-диференційним
рівнянням.
Таким його робить наявність похідної
![]() ,
яка є функцією інтегрального струму,
що протікає в електроліті уздовж осі
„х”:
,
яка є функцією інтегрального струму,
що протікає в електроліті уздовж осі
„х”:
![]() .
(6.18)
.
(6.18)
Тобто
для підрахування в кожній точці похідної
![]() потрібно мати інтеграл ще невідомої
функції
потрібно мати інтеграл ще невідомої
функції
![]() ,
яка сама є кінцевим рішенням рівняння
(6.17). Проте в ітераційному алгоритмі
рішення задачі ця особливість ненабагато
ускладнює роботу.
,
яка сама є кінцевим рішенням рівняння
(6.17). Проте в ітераційному алгоритмі
рішення задачі ця особливість ненабагато
ускладнює роботу.
Вираз
в квадратних дужках рівняння (6.17) – це
сумарний потік „g”
речовини уздовж осі „х”, моль/(с·см2),
тому рівняння можна записати коротше:
![]() .
Знак правої частини позитивний для
продуктів реакції, які накопичуються,
і негативний для витрачуваних реагентів.
.
Знак правої частини позитивний для
продуктів реакції, які накопичуються,
і негативний для витрачуваних реагентів.
В кожній точці глибини пор „х” потік „g” відображує інтегральний результат електрохімічного процесу, який здійснюється на ділянці електроду від х=0 до х:
![]() .
(6.19)
.
(6.19)
Як і в попередній задачі п.6.2, поляризацію відображує різниця потенціалів (U-V). В даному випадку поляризація є сумою активаційної та концентраційної складових і визначається класичним рівнянням змішаної кінетики (запис для реакції відновлення окисника „О”):
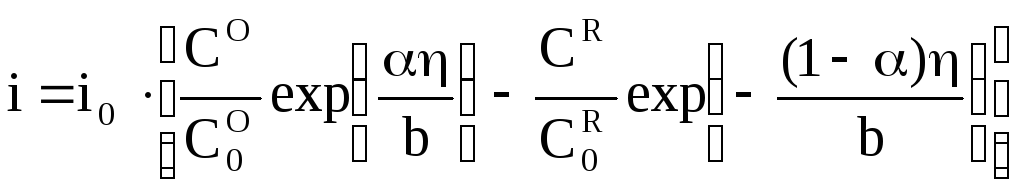 ,
(6.20)
,
(6.20)
де
і0
– густина струму обміну процесу, -
коефіцієнт переносу,
![]() ,
індексом „0” позначені концентрації
в об’ємі розчину, без індексу – в
поровому просторі на глибині „х”.
,
індексом „0” позначені концентрації
в об’ємі розчину, без індексу – в
поровому просторі на глибині „х”.
Алгоритм вирішення задачі.
Рівняння (6.20) вирішуємо також ітераційним алгоритмом. Для цього спочатку виконаємо диференціювання виразу в квадратних дужках
![]() ,
(6.21)
,
(6.21)
а потім переведемо його в різницеву форму
![]() ,
(6.22)
,
(6.22)
де
=dx
– крок дискретизації,
![]() -
градієнт потенціалу в електроліті, а
індекси n,
n-1,n+1
означають номери трьох сусідніх вузлів
по координаті товщини електроду x=0…h,
N=(h/
+1) – кількість вузлів. З цього рівняння
неважко одержати ітераційну формулу,
вирішуючи його відносно центрального
вузла n:
-
градієнт потенціалу в електроліті, а
індекси n,
n-1,n+1
означають номери трьох сусідніх вузлів
по координаті товщини електроду x=0…h,
N=(h/
+1) – кількість вузлів. З цього рівняння
неважко одержати ітераційну формулу,
вирішуючи його відносно центрального
вузла n:
![]() .
(6.23)
.
(6.23)
Такі формули виводять для всіх компонентів електроліту, в тому числі і нейтральних, які при умові v0=0 будуть переноситись лише фільтрацією та дифузією.
Граничні умові для цієї задачі визначаються умовами процесу. Наприклад, значення концентрацій в електроліті на фронтальній та тильній межах електроду. Якщо одна габаритна поверхня герметична і закрита для масообміну з розчином – граничною умовою буде для неї нульова похідна dC/dx.
Таким чином, повна математична модель процесу в пористому рідинному електроді містить два рівняння Пуассона (6.11) та систему рівнянь типу (6.20-6.23), кожне з яких відповідає одному з компонентів електроліту. Крім цього, в систему входить ще одне рівняння електронейтральності
![]() ,
(6.24)
,
(6.24)
згідно з яким в будь-якому перетині електроду сумарна концентрація зарядів має бути нульовою, незважаючи на те, що іони рухаються з різними швидкостями і в різних напрямках.
Алгоритм повинен виконувати такі дії.
1. Спочатку задають початкові довільні функції розподілу по глибині електроду локальних значень густини струму та концентрацій всіх компонентів.
2. Далі всі розрахунки виконують в ітераційному циклі, причому паралельно підраховують обидва поля потенціалів і концентраційні поля всіх компонентів. На кожному кроці ітераційного циклу підраховують значення параметрів у всіх 2...N-1 вузлах лінії опорів.
А- Підраховують інтегральний струм І, який протікає в електроліті і в твердій фазі в точці „х” (номер вузла nх ), за схемою рис. 6.2:
![]() ;
;
![]() . (6.25)
. (6.25)
Б-
За формулами (6.13) підраховують функції
розподілу потенціалів у вузлах 2..
N-1,
![]() .
Значення в першому і останньому вузлах
задані або визначаються граничними
умовами.
.
Значення в першому і останньому вузлах
задані або визначаються граничними
умовами.
В-
За формулами (6.23) підраховують функції
розподілу концентрацій усіх компонентів
у вузлах 2..
N-1,
![]() .
Значення в першому і останньому вузлах
також задані або визначаються граничними
умовами.
.
Значення в першому і останньому вузлах
також задані або визначаються граничними
умовами.
Г-
За рівнянням змішаної кінетики (6.20) ,
приймаючи
![]() ,
визначають функцію розподілу густини
струму
,
визначають функцію розподілу густини
струму
![]() .
.
Д-
Визначають сумарну концентрацію зарядів
![]() ,
і
якщо вона не нульова, коректують
індивідуальні концентрації іонів
(наприклад, штучно розподіляючи різницю
пропорційно концентраціям).
,
і
якщо вона не нульова, коректують
індивідуальні концентрації іонів
(наприклад, штучно розподіляючи різницю
пропорційно концентраціям).
Е- Перевіряють якість сходження ітерацій, порівнюючи між собою на двох сусідніх ітераціях або всі, або окремі функції розподілу параметрів по глибині пористого електрода. Якщо сходження досягнуто і функція співпадає з визначеною кроком раніше, процес припиняють.
3. Після закінчення ітераційного циклу рішення існує, і можна підрахувати інші важливі параметри процесу в порах – габаритний струм електрода ІФ (суму локальних струмів усіх вузлів), відношення габаритного струму ІФ до теоретичної максимальної величини ІМАХ (6.10), де ІМАХ = і1*N і т.д.
6.4. Стаціонарні транспортні процеси в пористих сепараторах
В технології широко використовують пористі сепаратори, які відокремлюють електроліти катодних і анодних камер і тим запобігають їх прямому змішуванню. Але через електроліт в поровому просторі сепаратор пропускає струм, фільтраційні і дифузійні потоки, лише частково гальмуючи їх. В стаціонарному режимі роботи електролізера внаслідок руху компонентів з однієї камери в іншу в сепараторі встановлюються деякі стаціонарні концентраційні профілі С(х) всіх компонентів.
Схема розташування сепаратора показана на рис. 6.6
Рис.
6.6. Схема роботи сепаратора. 1,2 – лівий
електрод і електродна камера, 3,4- правий
електрод і електродна камера, 5- сепаратор,
А,К- початкові (дифузійні) профілі
концентрацій
аніона та катіона. Стрілками вказані
знаки напрямків потоків
І в пористому електроді і в сепараторі закономірності переносу повністю ідентичні. Різниця полягає лише в тому, що в пористому сепараторі на внутрішній поверхні ніяка реакція не здійснюється. Тому потоки кожного компонента на обох поверхнях сепаратора однакові, а в рівнянні переносу (6.17) в правій частині має бути нуль:
![]() (6.26)
(6.26)
причому
тут градієнт потенціалу
![]() є просто параметр, який визначається
величиною густини струму і ефективною
електро-провідністю розчину в порах.
Густина струму в напрямі 0х постійна
величина, а питома електропровідність
змінюється уздовж координати, бо
змінюються концентрації компонентів
внаслідок переносу.
є просто параметр, який визначається
величиною густини струму і ефективною
електро-провідністю розчину в порах.
Густина струму в напрямі 0х постійна
величина, а питома електропровідність
змінюється уздовж координати, бо
змінюються концентрації компонентів
внаслідок переносу.
Математична модель і алгоритм. В сепараторі внаслідок одночасної дії на іонні компоненти електроліту закону електронейтральності і трьох механізмів переносу - міграції, дифузії та фільтрації, виникають складні нелінійні концентраційні профілі С(х), такі, що три складові частини швидкості кожного іона змінюються вдовж координати “х”, але в будь-якому перетині “х” його сумарний потік залишається незмінним. Підрахувати їх (а також потоки нейтральних речовин в молекулярній формі) за простими аналітичними формулами можна лише в окремих часткових випадках.Числовим моделюванням можна знайти точне рішення.
Рішення знаходять в N точках по товщині сепаратора. Iтераційним методом вирішується система рівнянь переносу (6.26) для всіх компонентів механізмами дифузії, фільтрації та міграції. Рівняння (6.26) переводять в дискретну (різницеву) форму, вирішують відносно концентрації у вузлі n і одержують спільну ітераційну формулу :
![]() ,
(6.27)
,
(6.27)
де С-концентрація компонента, z- його зарядове число (знак «+» або «-»), v=DzF/RT - рухомість іона (см/с), dU/dx=i/–градієнт потенціалу в електроліті в порах, - питома електропровідність розчину в точці 0<x<L, =L/(N-1) - крок дискретизації (dx), N- кількість точок по координаті “х”. Параметри jF , є спільними, а z,v – індивідуальні для кожного іона.
Складовою частиною системи рівнянь є рівняння електронейтральності (6.24), яке означає рівність сумарних концентрацій аніонів і катіонів в будь-якій точці координати «х» (в перетині сепаратора площиною, паралельною його зовнішній габаритній поверхні).
Граничні умови - задані концентрації всіх компонентів в правій (Р) та лівій (L) камерах.
Залежність питомої електропровідності електроліту від сумарної іонної концентрації CS можна використати як апроксимаційний поліном другого ступеню (парабола) з трьома коефіцієнтами а1,а2,а3:
![]() .
(6.28)
.
(6.28)
Послідовність обчислювальних операцій така ж, як в інших алгоритмах.
1. Задають початкові довільні функції розподілу по глибині електроду локальних значень концентрацій всіх компонентів.
2. Далі всі розрахунки виконують в ітераційному циклі:
А-
За формулами (6.26) підраховують функції
розподілу концентрацій компонентів
у вузлах 2..
N-1,
![]() .
Значення в першому і останньому вузлах
задані
.
Значення в першому і останньому вузлах
задані
Б-
Визначають сумарну концентрацію зарядів
![]() ,
і якщо вона не нульова, коректують
індивідуальні концентрації іонів, як
було показано в п.6.3.
,
і якщо вона не нульова, коректують
індивідуальні концентрації іонів, як
було показано в п.6.3.
В- Визначають потоки gi окремих компонентів за виразом в квадратних дужках в (6.26). Для контролю можна визначати цей параметр, наприклад, в різних точках осв 0х – на лівій та на правій межі, в середині. Ці величини для кожного іона повинні бути однаковими.
Г- Перевіряють якість сходження ітерацій, порівнюючи між собою на двох сусідніх ітераціях наприклад, або всі, або окремі значення іонних потоків або концентрацій. Якщо сходження досягнуто і функція співпадає з визначеною кроком раніше, процес припиняють.
Кінцевим результатом рішення є функції розподілу концентрацій по товщині сепаратора С(х) для всіх компонентів реакції а також їх потоки через сепаратор з однієї камери в протилежну.
На
рисунку 6.7 наведено приклад розрахованих
концентраційних профілів в електроліті![]() ,
який містить чотири види іонів різних
знаків (
нумерація
кривих 1-H+,
2-Cu2+
, 3-Zn2+,
4-SO42-).
В правій електродній камері (катод
Cu0/Cu2+
елемента Даніеля-Якобі) міститься розчин
,
який містить чотири види іонів різних
знаків (
нумерація
кривих 1-H+,
2-Cu2+
, 3-Zn2+,
4-SO42-).
В правій електродній камері (катод
Cu0/Cu2+
елемента Даніеля-Якобі) міститься розчин
![]() ,
в лівій (анод Zn0/Zn2+)
-
,
в лівій (анод Zn0/Zn2+)
-![]() .
Напрямок руху катіонів в сепараторі –
зліва направо, він визначений напрямком
струму при розряді елемента.
.
Напрямок руху катіонів в сепараторі –
зліва направо, він визначений напрямком
струму при розряді елемента.
Рис.6.7.
Концентраційні профілі чотирьох видів
іонів

З форми профілю кривої 2 (Cu2+) видно, що справа існує досить сильний дифузійний потік іонів Cu2+ в сепаратор через великий градієнт концентрації. Але він повністю компенсується зустрічним міграційним потоком, тому в даному випадку іони міді в ліву (анодну) камеру не проникають – це видно з того, що в лівій частині концентрація іонів Cu2+ практично нульова.
