5. Електричні поля в електрохімічних системах

В технічній електрохімії існує багато об’єктів, в яких окремі параметри мають різні значення в різних точках внутрішнього геометричного простору, тобто є деякими функціями координат. Наприклад, густина струму і поляризація зменшуються по глибині пористого електроду, змінюються концентрації речовин уздовж апарата витискування, тощо. Такі технічні системи називають системами з розподіленими параметрами.

Якщо є формальна залежність деякої величини U від геометричних координат, U=f(x,y,z) , таку залежність називають полем величини U. Коли величина U є функцією всіх трьох координат (x,y,z), поле називають тривимірним. В тривимірному полі параметр U змінюється в об’ємі, тобто по всіх координатах. Поля U=f(x,y) та U=f(x) будуть відповідно двовимірним та одновимірним.

В окремих випадках реальні тривимірні поля можна відносно спрощено розглядати з меншою кількістю вимірів. Таких випадків можна розглянути три.

1. Існують такі об’єкти, у яких уздовж однієї з координат (z) параметр U (потенціал) має постійне значення. Це поле має назву «плоскопаралельне поле». Хоч таке поле насправді є тривимірним, його можна розглядати як плоске (двовимірне). В електрохімічній практиці такі властивості характерні для електричного поля в електроліті електролізеру, якщо електроди розташовані вертикально на всю глибину, а висота шару електроліту набагато менша за довжину і ширину (рис.5.1а).

Рис.5.1. Варіанти полів зі зменшеною розмірністю. а-плоскопаралельне, б- з циліндричною симетрією, в-з сферичною симетрією.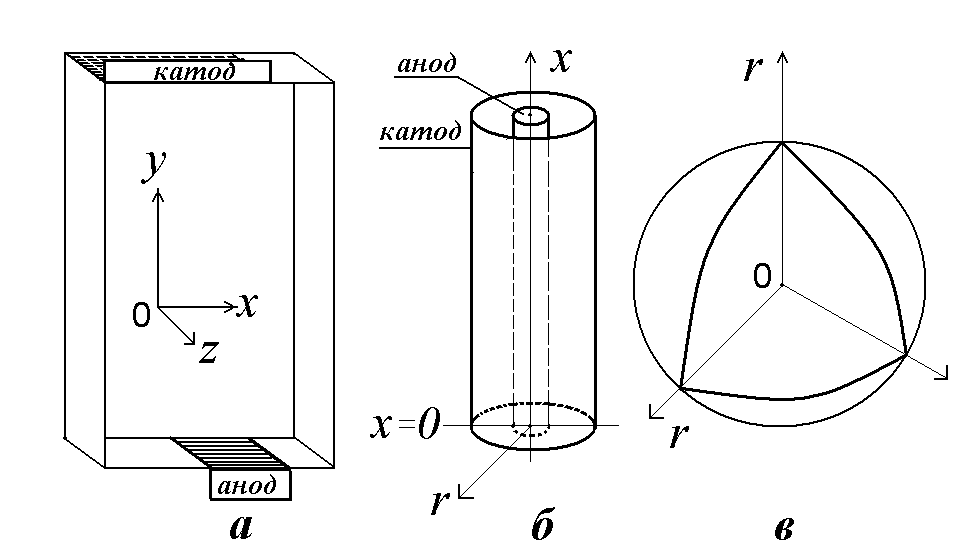

2. Циліндричне поле (рис.5.1б) виникає в системах з циліндричною симетрією (наприклад, при анодуванні дроту в електролізері з катодом трубчастої форми). Тут параметр поля змінюється по двох координатах –по довжині „х” та по радіусу „r”.

3. Сферичне поле (рис.5.в). Виникає в системах з сферичною симетрією, змінюється лише по одній координаті – радіусу „r”. В електрохімії таку форму має електричне поле одиничного іона та іонної атмосфери.

Поле, в якому його характеристика постійна (U=const), називають однорідним.

В залежності від того, про який параметр іде мова, поля можуть бути скалярні або векторні.

Векторні величини, на відміну від скалярних, визначаються (в двовимірному полі) двома числами: це або дві проекції на осі х та y, або ж модуль (абсолютне значення) та напрямок вектора (кут , який утворений вектором з віссю Ох, рис. 5.2б).

5.1. Двовимірне електричне поле.

В цьому розділі ми розглянемо найпростішу задачу про електричне поле, яке виникає в тонкій прямокутній пластині HGh, h<<G,H з питомим опором =1/ Ом·см (- питома електропровідність, См/см). Пластинку можна розглядати як звичайний провідник, до якого за допомогою двох контактів, довільно розташованих на контурі, накладають напругу U₂-U₁ і. пропускають струм I (рис.5.2).

Рис.5.2. Графічне зображення плоскопаралельного поля потенціалу і поля струму (штрихові лінії).

Густина струму нерівномірно розподіляється в пластині, тому неможливо використати просту формулу закону Ома I=U/R та R=·L/S, бо в цих умовах, як видно з рисунка 5.2, не існує якогось конкретного значення L ( довжина шляху струму), та S (площа перетину потоку зарядів). Для того, щоб підрахувати величину струму в цій задачі, необхідно спочатку вирішити задачу визначення електричного поля.

Електричне поле – це поле потенціалу U=f(x,y,z). Потенціал є скалярною величиною, він характеризує роботу, яку виконує електричний заряд при переміщенні в дану точку поля (x,y,z).

Неоднорідне електричне поле, в якому потенціал змінюється в просторі, виникає в середовищі, яке чинить опір рухові зарядів. Щоб пояснити механізм виникнення такого поля, розглянемо в електропровідному середовищі елементарний кубик з ребром x. Припустимо, що через нього перпендикулярно одній з граней в напрямку осі «х» проходить струм густиною «і». Для цього кубика можна записати рівняння закону Ома в диференційній формі:

. (5.1)

Енергія електричного поля витрачається на подолання опору середовища. Внаслідок цих втрат потенціал U зменшується на величину U= U_x+х – U_x , на що вказує знак «–» градієнта потенціалу. Інакше кажучи, потенціал зменшується в напрямку руху зарядів, тим сильніше, чим більший питомий опір середовища, і чим довший шлях х, який проходить струм:

(5.2)

Електричне поле вважається визначеним, якщо відома функція U=f(x,y,z). Дійсно, тоді для будь-якої точки (x,y,z) можна за правилами векторної алгебри підрахувати величину і напрям струму. На рис.5.3а наведений фрагмент дискретного електричного двовимірного поля потенціалу U. Термін „дискретне поле” означає, що воно представлене не неперервною функцією U(x,y), а лише окремими її значеннями в точках з інтервалами х=y по координатах. Саме таке дискретне поле підраховують алгоритмами числового моделювання на ЕОМ.

Рис. 5.3. Визначення напряму струму і градієнта потенціалу двовимірного електричного поля.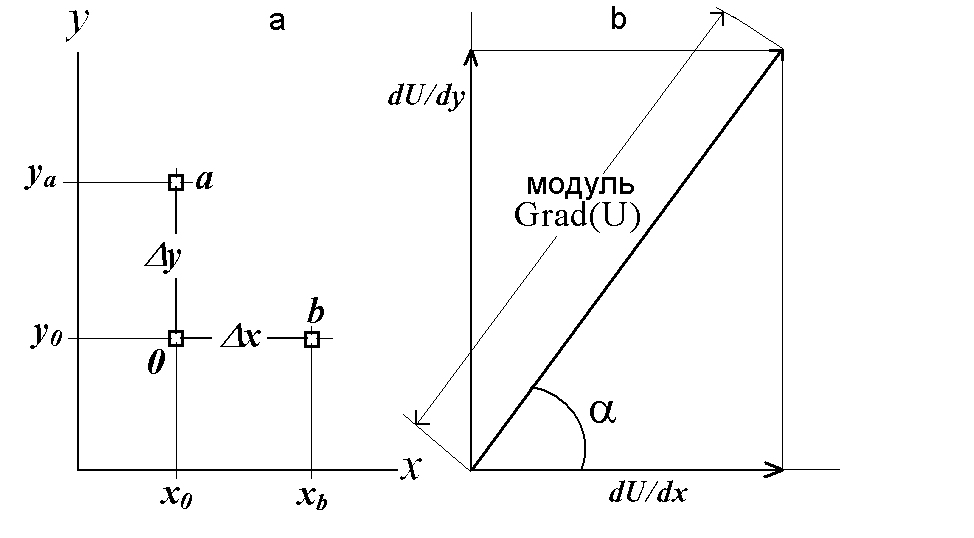

Оберемо три сусідні точки поля, позначені на рисунку 5.3.а буквами О, а, b. В цих точках відомі значення потенціалів U₀, U_a, U_b. З них можна визначити часткові похідні потенціалу по обох координатах

, . (5.2)

Вони є проекціями на осі x та y векторної величини – градієнта потенціалу grad(U). Його модуль згідно правил векторного складання визначається за теоремою Піфагора як довжина діагоналі прямокутника (рис.5.3 b).

. (5.3)

Градієнт потенціалу вказує напрямок найшвидшої зміни потенціалу, а його модуль – числове значення зміни потенціалу в цьому напрямку. Назва-синонім градієнта потенціалу – напруженість поля. Напруженість поля – це сила, яка діє на одиничний заряд в даній точці поля і викликає його рух. Оскільки рух зарядів – це струм, то напрямок градієнта потенціалу одночасно є напрямком руху електричних зарядів, тобто напрямком струму в даній точці. Струм, таким чином, теж є векторною величиною, і закон Ома (5.1) для векторного поля можна записати аналогічно:

(5.4)

Рівняння (5.1) є частковим випадком (5.4) для умови, коли напрямок струму співпадає з напрямком осі „х”, тоді . Аналогічно і струм з довільним напрямком можна представити як векторну суму його проекцій на обидві осі:

, , (5.5)

Таким чином в усіх практичних задачах головною метою є визначення електричного поля в формі функції U=f(x,y,z), з якої можна розрахувати всі інші електричні параметри системи, а також окремі поля – поле градієнта потенціалу та поле струму.

Графічне зображення електричного поля. Електричне (двовимірне) поле потенціалу U(x,y) можна представити в графічній формі як деяку поверхню функції U в декартових прямокутних координатах x, y, z=U. Простіше цю поверхню зобразити як систему ізоліній U=const на площині (x,y) , тобто як проекції перетинів поверхні U(x,y) площинами, паралельними площині (x,y). Саме так зображують поле висот або глибин земної поверхні на географічних картах. На рис.5.2 показано приклад такого зображення поля потенціалів в прямокутній електропровідній пластині з двома контактами, показаними на контурі, через які підводять напругу U₂-U₁.

Кількість еквіпотенціальних ліній К (на рисунку 30) довільна і залежить від того, з яким кроком U=const їх будувати: К=(U₂-U₁)/ U.

Оскільки значення мають не самі потенціали, а їх різниці між двома точками, зручно за нуль U=0 прийняти значення в якій-небудь точці, і називати терміном „потенціал” різницю U(x,y)-U. Приймемо в даному випадку потенціал лівого струмопідводу U₁=0, тоді U₂ – потенціал правого струмопідводу, а різниця (U₂–U₁)= U₂ є напругою, прикладеною до пластинки.

Поле струму зображується на площині лініями струму. Це лінії, які показують напрямок руху зарядів. Згідно з рівнянням (5.4) напрямок струму співпадає з напрямком градієнта потенціалу. Лінію струму можна провести через будь-яку точку поля (x,y) як лінію, що починається на одному струмопідводі і закінчується на другому, і перпендикулярну до еквіпотенціальних ліній. На рис.5.2 наведено пунктиром дві лінії струму. Область між ними називають трубкою струму . Через трубку струму рухається потік зарядів, не перетинаючи обмежуючих ліній струму, тобто струм однаковий в будь-якому перетині трубки. Тому зображення поля наочно показує , як розподіляється густина струму – вона більша там, де площа перетину трубки менша, тобто там, де спостерігається згущення всіх ліній – потенціалу і струму. З рисунка видно, що згущення ліній поля спостерігається поблизу струмопідводів.

Еквіпотенціальні лінії не перетинаються між собою, вони входять в контур пластинки перпендикулярно. Це означає, що перпендикулярний до них контур є лінією струму, тобто струм протікає в пластинці, не перетинаючи межу електропровідного середовища- в даному випадку контур пластинки.

Математична модель електричного поля. Електричне поле описується диференційним рівнянням другого порядку в часткових похідних – рівнянням Лапласа, яке для тривимірного та двовимірного електричного поля має форму :

, . (5.6)

Зрозуміло, чому в (5.6) для плоскопаралельного поля відсутній третій доданок – бо для постійної величини () обидві похідні, та , дорівнюють нулю.

Для того, щоб зрозуміти фізичний зміст рівняння Лапласа, розглянемо дискретну двовимірну модель електропровідної пластинки (рис. 5.4) .

Рис.5.4. Фрагмент дискретної сіткової моделі тонкої прямокутної пластинки.

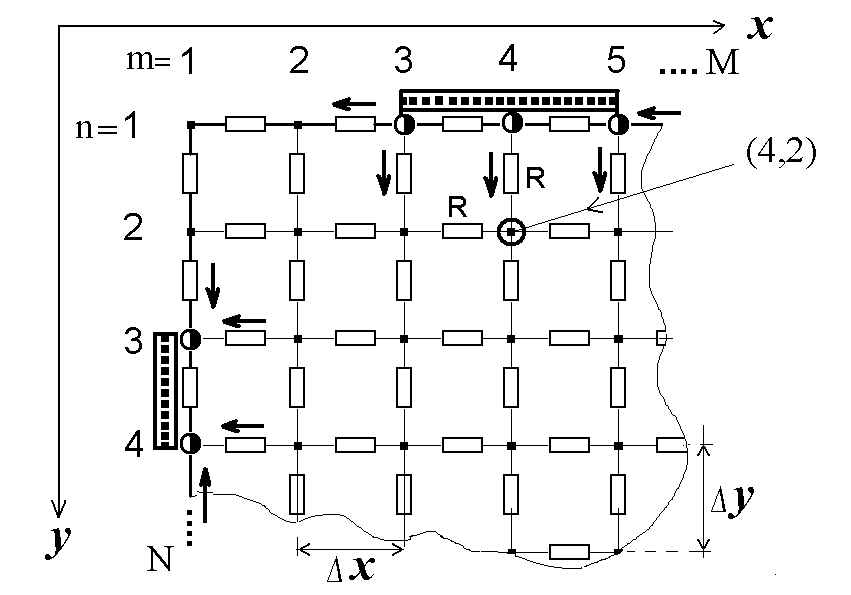
Модель представляє собою двовимірну систему точок-вузлів, розташованих у кутах елементарних клітинок. Такі вузли утворюються на перетинах М вертикальних і N горизонтальних ліній, якими умовно можна розділити пластинку на (N-1)(М-1) елементарних квадратних клітинок розміром xy (x=y) . Всі вузли між собою з’єднані резисторами R. Величина опору R, Ом, визначається як опір елементарної клітинки пластинки товщиною h:

. (5.7)

З формули можна бачити цікаву особливість цього опору (він має спеціальну назву розмірності „Ом на квадрат”) - він не залежить від розміру квадрата x=y. Для наступного моделювання поля це означає, що розраховане електричне поле (значення потенціалів у всіх вузлах поля) не залежить від розміру елементарного квадрата x=y , тобто кількості вузлів. Розмір x=y впливає лише на точність результату – чим ближче розташовані вузли між собою, тим точніший результат, бо значення потенціалу поля підраховуються лише у вузлах.

Візьмемо для прикладу будь-який вузол з чотирма сусідніми найближчими вузлами (рис.5.5) і запишемо для нього рівняння балансу струмів згідно з законом Кірхгофа:

. (5.7)

Рис.5.5. Струми у окремому вузлі „0” сіткової моделі.

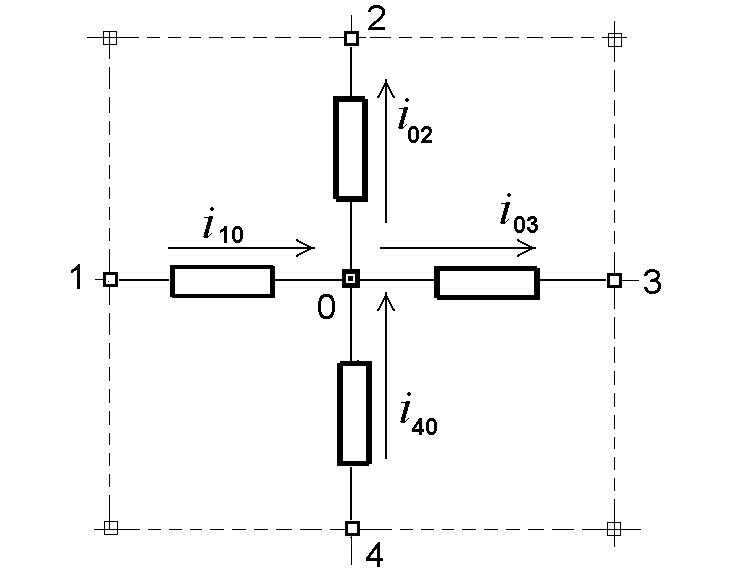
Закон Кірхгофа є законом збереження кількості заряду– у вузлі „0” заряд не накопичується і не генерується, тому сума всіх струмів, які протікають через вузол „0”, дорівнює нулю.

Згідно з законом Ома струми в рівнянні Кірхгофа можна переписати через потенціали U вузлів, наприклад для лінії 1-0:

(5.8)

При умові х0 можна здійснити заміну , , , тоді рівняння (5.8) матиме диференційну форму

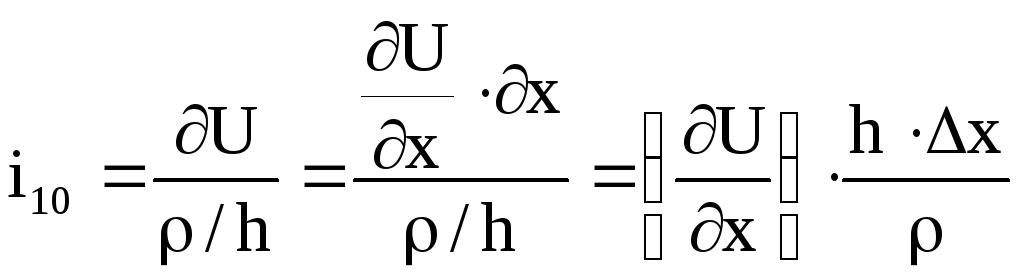. (5.9)

Якщо таким же чином переписати вирази типу (5.9) для всіх струмів, урахувати умову (сторона елементарного квадрата) та підставити в рівняння Кірхгофа, одержимо

. (5.10)

Далі можна розділити обидві частини рівняння (5.10) на , і замінити різниці перших похідних другими , , тоді матимемо рівняння Лапласа:

. (5.11)

Перехід від рівняння (5.7) до (5.11) означає, що це є одне і те ж рівняння закону збереження заряду. Перша форма Кірхгофа (5.7) алгебраїчна і відповідає параметрам (струми і потенціали) сіткової дискретної моделі двовимірного електричного поля. Друга диференційна форма рівняння Лапласа (5.6, 5.11) записана для неперервного електричного двовимірного поля.

Граничні умови. Всі задачі розрахунку електричних полів вирішуються для точно оговореного простору з визначеною геометричною формою та розмірами. В нашому прикладі це прямокутна пластинка з розмірами , , де =x=y.

Граничними умовами для розглянутої задачі є нульові значення перших похідних потенціалу на всіх чотирьох лініях периметра прямокутника (за виключенням вузлів-струмопідводів, де потенціали відомі, U₁= 0 та U₂):

;; ; . (5.12)

Нульові значення проекцій градієнту потенціалу на осі x,y означають згідно з виразом (5.4), що і відповідні проекції вектора струму ( і_х та i_y) також дорівнюють нулю на периметрі. Це очевидний факт – струм не виходить за межі пластинки.

Алгоритм визначення потенціалів поля. Для вирішення задачі спочатку перепишемо рівняння Кірхгофа через потенціали вузлів (нумерація вузлів по рис. 5.5):

. (5.13)

Вирішуючи його відносно потенціалу центрального вузла, одержимо іншу форму запису рівняння Кірхгофа:

, (5.14)

тобто потенціал кожного вузла сітки є середнім арифметичним від потенціалів чотирьох найближчих сусідніх вузлів.

Останню форму використаємо у ітераційному алгоритмі для числових розрахунків потенціалів у вузлах. Алгоритм виконує дії в такій послідовності.

1- Задають початкові дані:

а-значення потенціалів у вузлах, які належать струмопідводу на контурі, одного – нулі (точки n=3,4 на вертикалі m=1), другого – значення U₂ (точки m =3,4,5 на горизоналі n =1).

б- значення потенціалів у всіх інших вузлах,– будь-які числа, менші за U₂ (нульове наближення).

2- Далі в ітераційному циклі повторюють такі операції:

а) Перераховують за рівнянням (5.14) по черзі потенціали всіх внутрішніх вузлів сітки (це вузли, які не належать контурним лініям, у кожного є по 4 сусідніх вузли, як на рис. 5.5);

б) Перераховують потенціали усіх вузлів на 4-х лініях контуру ячейки, за виключенням „струмопідвідних” вузлів, бо там задані постійні значення потенціалів. Тут рівняння (5.14) непридатне, бо у контурного вузла сусідніх вузлів лише 3. Тому у відповідності з граничними умовами (5.12) підрахунок виконують так: потенціалу контурного вузла присвоюють значення потенціалу найближчого внутрішнього вузла. Наприклад за рис. 5.4 потенціал контурного вузла U(m=1,n=2) повинен бути рівним потенціалу внутрішнього вузла U (m=2,n=2);

в) Підраховують за законом Ома повний струм , який переходить з найближчих вузлів до обох „струмопідвідних”. Наприклад, для лівого струмопідводу (товсті стрілки на рис.5.4):

(5.15)

де за початковою умовою U₁₃ та U₁₄ – нулі. Це число і є кінцевим результатом розрахунку.

г) Перевіряють сходження ітераційного процесу за яким-небудь критерієм. Наприклад, порівнюючи струми обох струмопідводів – при одержанні точного рішення вони повинні бути однаковими. Ітераційний процес закінчується, коли різниця між ними на двох чергових кроках зменшується до заданого допустимого рівня помилки.