2.4.6. Асимптоты графика функции

Построение графика функции облегчается, если знать его асимптоты.

Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от переменной точки на графике до прямой стремится к нулю при неограниченном удалении точки по графику от начала координат (т.е. при стремлении аргумента к бесконечности).

Различают вертикальные и наклонные асимптоты. Частным случаем наклонной асимптоты является горизонтальная асимптота.

Прямая называется вертикальной асимптотой графика функции , если .

Вертикальные асимптоты проходят через точки бесконечного разрыва функции. Поэтому вертикальные асимптоты график функции может иметь только в точках разрыва второго рода или на границах области определения.

Наклонные асимптоты получают при исследовании поведения функции на бесконечности.

Уравнение наклонной асимптоты имеет вид , где

, .

Указанные пределы нужно находить отдельно при и.Если эти пределы будут различными, то график функции имеет две различные наклонные асимптоты: левостороннюю при и правостороннюю при . Если эти пределы равны при и, то функция имеет одну наклонную асимптоту.Если хотя бы один из указанных пределов, при отыскании и равен или не существует, то наклонных асимптот нет.

В частном случае, если , а, график функции имеет горизонтальную асимптоту, уравнение которой . Это прямая, параллельная оси .

Пример 21.

Найти асимптоты графика функции .

Решение.

Функция определена на всей числовой оси, кроме . Область определения функции имеет вид: .

Следовательно, точка – точка разрыва функции. Исследуем точку разрыва и вычислим односторонние пределы функции в указанной точке.

; .

Так как односторонние пределы равны , то в точке функция имеет разрыв второго рода. Соответственно график функции имеет вертикальную асимптоту (ось).

Возможное уравнение наклонной асимптоты будем искать в виде . Вычислим значения параметров и (для дробно-рациональной функции пределы будут одинаковы при ).

;

.

Подставляя найденные значения и, получим уравнение наклонной асимптоты .

График функции показан на рис.8

2.4.7. Полное исследование функции и построения ее графика.

Для построения графика функции необходимо выяснить его характерные особенности, т.е. исследовать функцию. Полное исследование функции проводят по следующей схеме:

1. Найти область определения функции.

2. Исследовать функцию на непрерывность. Найти вертикальные асимптоты.

3. Исследовать функцию на чётность и нечётность.

4. Исследовать функцию на периодичность.

5. Найти точки пересечения графика функции с осями координат.

6. Определить промежутки монотонности и экстремумы функции.

7. Определить промежутки выпуклости, вогнутости и точки перегиба.

8. Найти наклонные асимптоты графика функции. Если график не имеет наклонных асимптот исследовать поведение функции при .

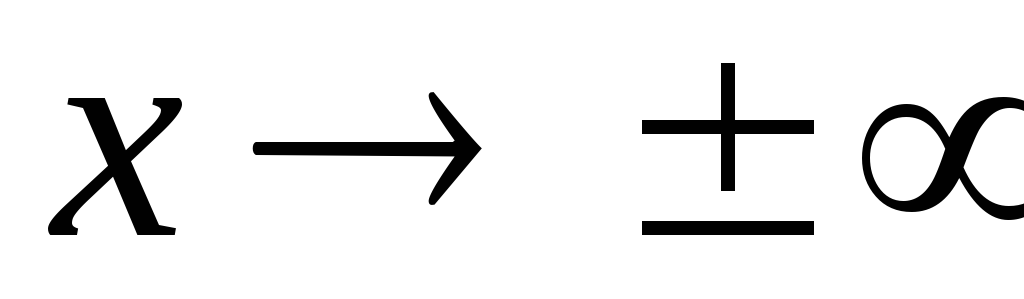9. Построить график функции (при необходимости найти дополнительные точки графика функции).

Пример 22.

Провести полное исследование функций и построить их графики:

а) ; б).

Решение.

а) .

1. Область определения функции.

Функция определена при всех значениях , кроме тех, в которых знаменатель обращается в ноль, т.е.

, .

Область определения функции .

2. Непрерывность функции.

Функция определена при всех значениях , кроме . Следовательно, точки и – точки разрыва функции. Исследуем точки разрыва, найдем односторонние пределы функции в указанных точках.

;

;

;

.

Так как односторонние пределы равны , то в точках и функция терпит разрыв второго рода. Следовательно, график функции имеет две вертикальные асимптоты и .

3. Четность, нечетность.

Так как , то функция нечетная и ее график симметричен относительно начала координат.

4. Периодичность.

Так как не существует значения , при котором выполняется равенство , то функция непериодическая.

5. Точки пересечения с осями координат.

Точки пересечения графика функции с координатными осями ищем, приравнивая аргумент и функцию нулю.

С осью : ;;.

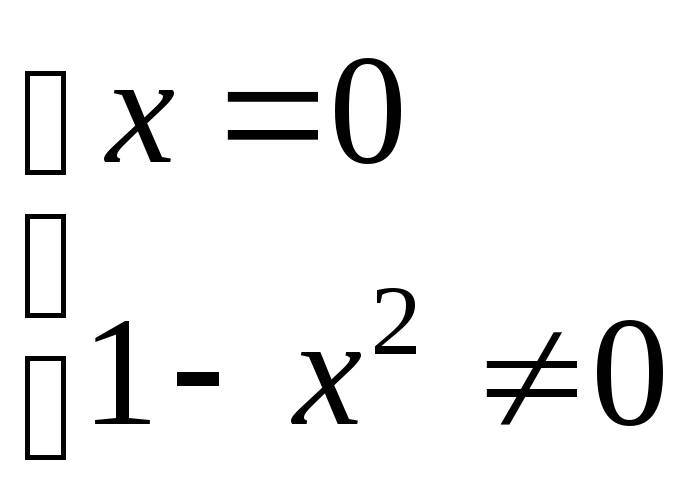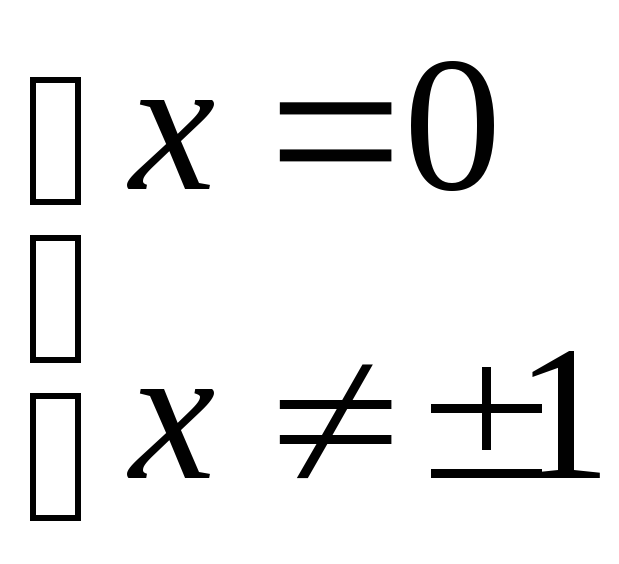Точка пересечения графика функции с осью имеет координаты: .

С осью : .

Точка пересечения графика функции с осью имеет координаты: .

Следовательно, график функции проходит через начало координат, других точек пересечения графика функции с координатными осями нет.

6. Промежутки возрастания, убывания функции, экстремумы.

Найдем первую производную:

.

Найдем критические точки первого рода:

; .

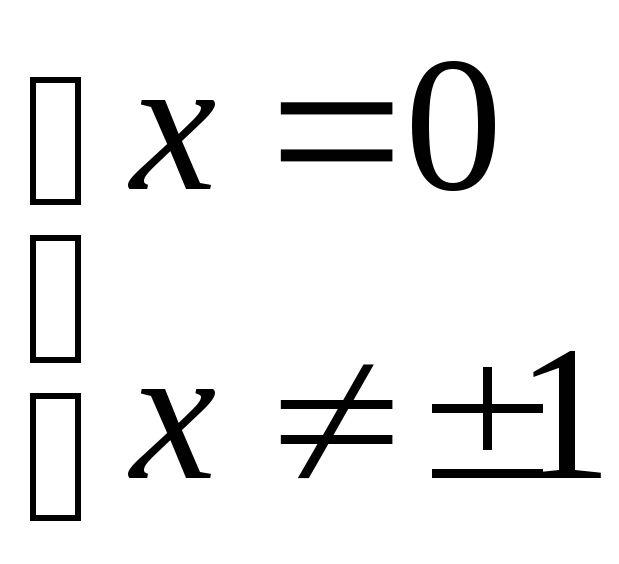Разобьем область определения критическими точками первого рода на интервалы и определим в каждом из них знак производной .

		– 1		0		1
	+	не сущ.	+	0	+	не сущ.	+
	↗	не сущ.	↗	0	↗	не сущ.	↗

Так как при переходе через критическую точку производная не меняет знак, то экстремума нет.

7. Промежутки выпуклости, вогнутости, точки перегиба.

Найдем вторую производную:

.

Найдем критические точки второго рода: ;

; ;.

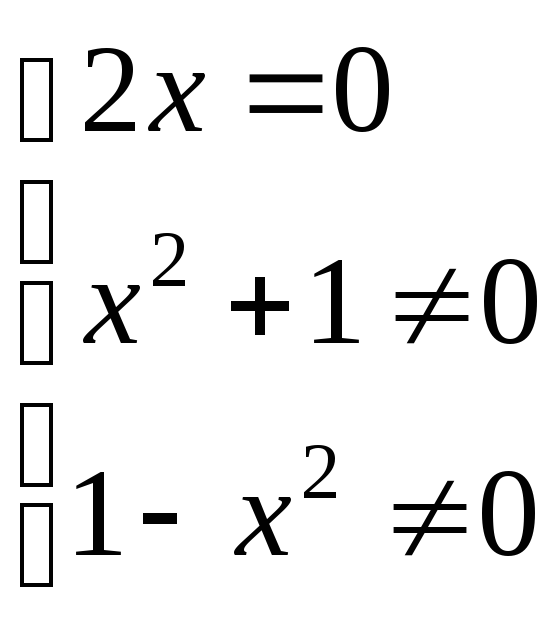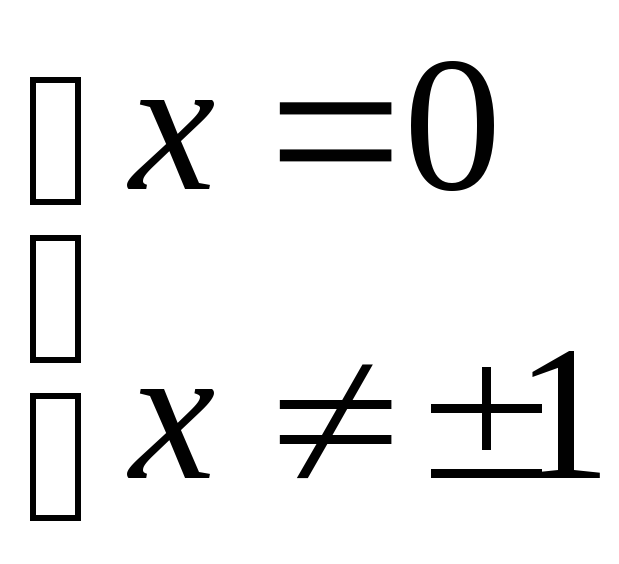Разобьем область определения критическими точками второго рода на интервалы и определим в каждом из них знак второй производной .

		– 1		0		1
	+	не сущ.	–	0	+	не сущ.	–
		не сущ.		0		не сущ.	

точка

перегиба

Так как при переходе через критическую точку вторая производная меняет знак, то – абсцисса точки перегиба. Точка перегиба: .

8. Наклонные асимптоты.

Уравнение наклонной асимптоты будем искать в виде . Вычислим значения параметров и (для дробно-рациональной функции пределы будут одинаковы при ).

;

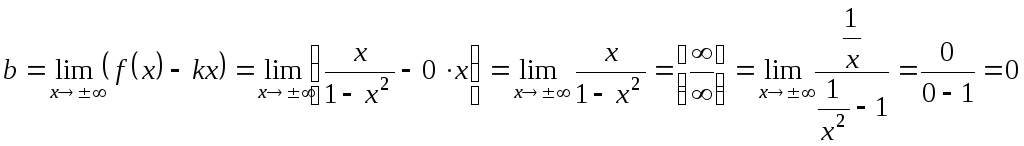
Так как и, то график функции имеет горизонтальную асимптоту (ось).

9. Построение графика.

Построим график функции, учитывая пункты 1–8 (рис. 9).

Дополнительно найдем несколько точек графика функции:

	–3	–2	–1,5	–0,5	0,5	1,5	2	3
	0,38	0,67	1,2	–0,67	0,67	–1,2	–0,67	–0,38

б) .

1. Область определения функции.

Логарифмическая функция определена при, кроме этого знаменатель не может равняться нулю, т.е..

Тогда область определения функции имеет вид: .

2. Непрерывность функции.

Так как функция не определена в точке , то это точка разрыва. Исследуем характер точки разрыва, найдем односторонние пределы функции.

;

.

Так как односторонние пределы равны , то в точке функция терпит разрыв второго рода. Следовательно, функция в этой точке имеет вертикальную асимптоту .

Исследуем также поведение функции на границе области определения:

.

Значит при справа график функции стремится в точку .

3. Четность, нечетность.

Так как и, то функция ни четная ни нечетная, т.е. общего вида.

4. Периодичность.

Так как не существует значения , при котором выполняется равенство , то функция непериодическая.

5. Точки пересечения с осями координат.

С осью :;;.

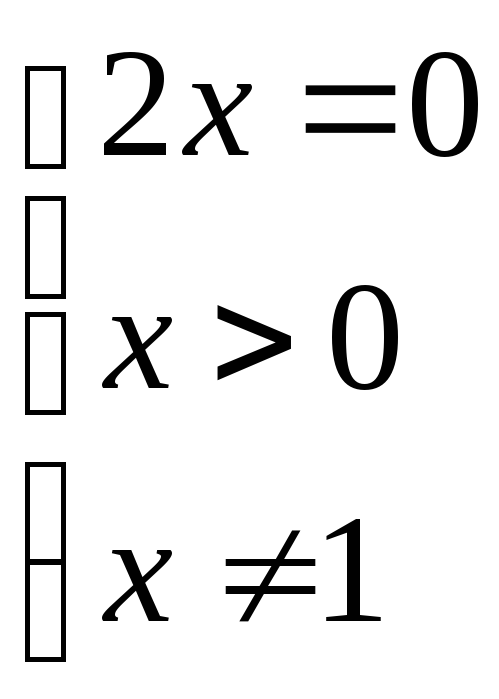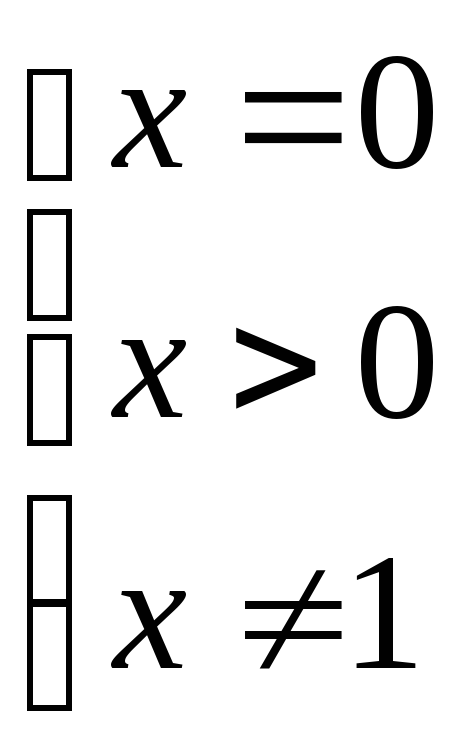Так как полученная система не имеет решений, значит точек пересечения графика с осью нет.

С осью : так какне входит в область определения, то точек пересечения с осьюнет.

График функции не пересекает координатные оси.

6. Промежутки возрастания, убывания функции, экстремумы.

Найдем первую производную:

.

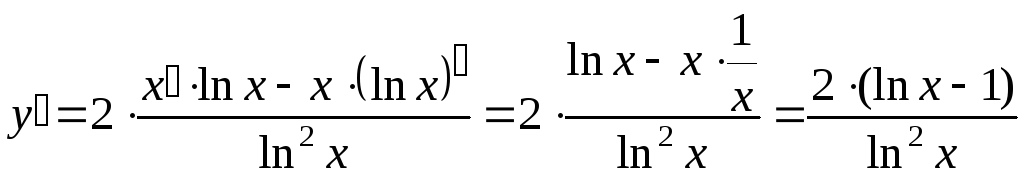Найдем критические точки первого рода:

; ;;.

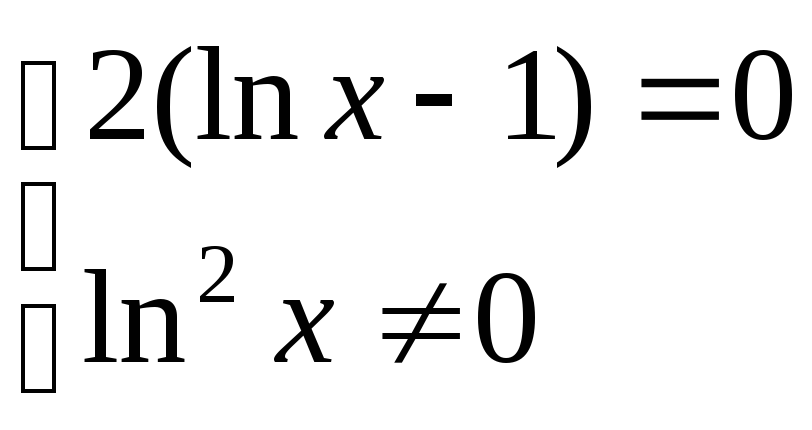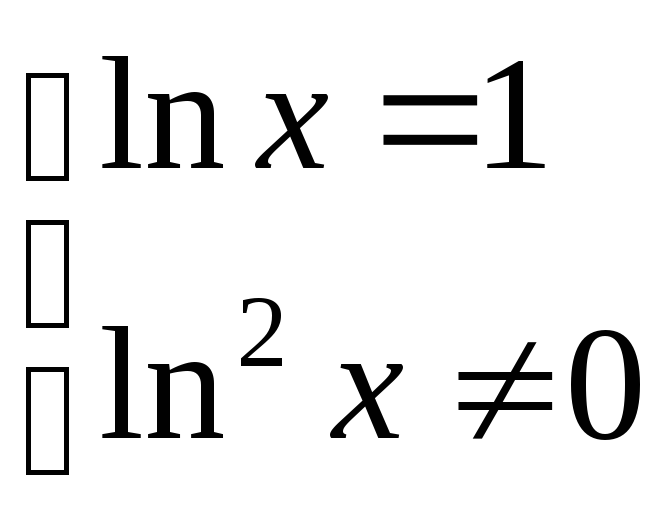Разобьем область определения критическими точками первого рода на интервалы и определим в каждом из них знак производной .

		1		е
	–	не сущ.	–	0	+
	↘	не сущ.	↘	2е	↗

min

Так как при переходе через критическую точку производная меняет знак с «–» на «+», то в этой точке – минимум функции.

Найдем значение функции в точке :.

7. Промежутки выпуклости, вогнутости, точки перегиба.

Найдем вторую производную:

.

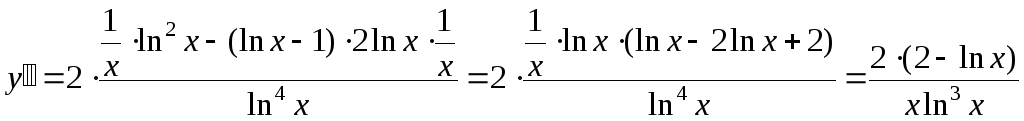Найдем критические точки второго рода: .

; ;.

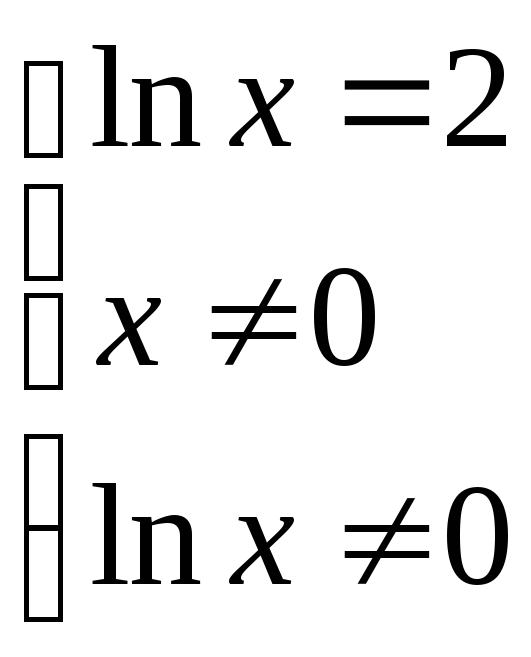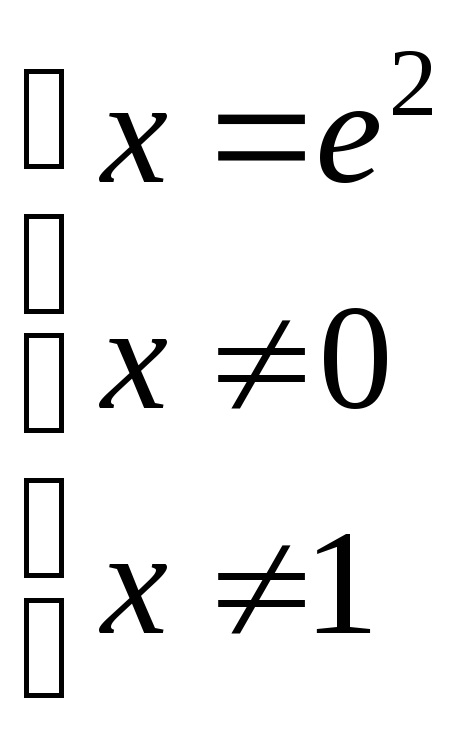Разобьем область определения критическими точками второго рода на интервалы и определим в каждом из них знак второй производной .

		1
	–	не сущ.	+	0	–
		не сущ.		е2	

точка

перегиба

Так как при переходе через критическую точку вторая производная меняет знак, то – абсцисса точки перегиба.

Найдем значение функции в точке :

.

8. Наклонные асимптоты.

Вычислим значения параметров и (учитывая область определения функции можно рассматривать лишь случай при).

;

.

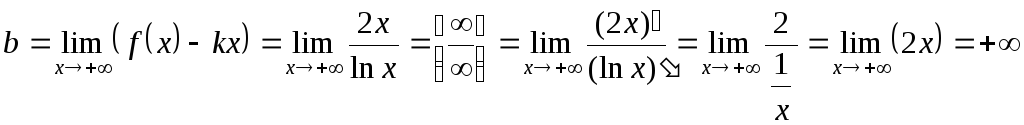Так как , то график функции наклонных асимптот не имеет.

Исследуем поведение функции при :

(см. выше нахождение параметра ).

9. Построение графика.

Построим график функции, учитывая пункты 1–8 (рис. 10).

Дополнительно найдем несколько точек графика функции:

	0,5	1,5	2	5	8	11
	–1,44	7,4	5,77	6,21	7,69	9,11