2.2. Общие правила дифференцирования функции.
Таблица производных.
Нахождение производной называется дифференцированием функции. При определении производных пользуются правилами дифференцирования, а также таблицей производных.
Таблица производных основных элементарных функций
1.
,
(
); 5.
;
2.
; 6.
;
2.
,
(
); 7.
;
2.
; 8.
;
3.
; 9.
,
(
);
3.
; 10.
,
(
);
4.
; 11.
;
4.
; 12.
.
Основные правила дифференцирования
Пусть
и
–
дифференцируемые функции,
– постоянная. Тогда:
,
(производная постоянной величины равна
нулю);
2) 
,
(постоянный множитель можно выносить
за знак производной);
,
(производная алгебраической суммы
функций равна алгебраической сумме
производных);
,
(производная произведения двух функций
равна произведению производной первой
функции на вторую плюс произведение
производной второй функции на первую);
5) 
,
(производная частного двух функций
равна дроби в числителе которой –
произведение производной числителя на
знаменатель минус произведение
производной знаменателя на числитель,
а в знаменателе – квадрат знаменателя).
Производная сложной функции
Пусть
и
.
Тогда
есть сложная
функция с
промежуточным аргументом
и основным аргументом
.
Производная сложной функции определяется по формуле:
.
Функция
дифференцируется по
,
а
дифференцируется по
.
Эта формула распространяется на любую цепочку из любого конечного числа дифференцируемых функций.
Замечание:
На практике при дифференцировании
сложной функции полезно выделять
«внешнюю» функцию
и «внутреннюю» функцию
.
Дифференцирование начинается всегда
с внешней функции, а внутренняя функция,
как бы громоздко она ни выглядела,
считается простым аргументом. Производная
внутренней функции находится по обычным
правилам.
Таким образом, учитывая правило нахождения производной сложной функции, таблицу основных элементарных функций можно записать в расширенном виде.
Сводная таблица формул дифференцирования
1.
,
(
); 5.
;
2.
; 6.
;
2.
; 7.
2.
; 8.
3.
; 9.
;
3.
; 10.
;
4.
; 11.
;
4.
; 12.
.
Пример 10.
Найти производные сложных функций:
а)
; б)
;в)
;
г)
;д)
;е)
;
ж)
;з)
; и)
.
Решение.
а)
.
б)
.
в)
.
г)
.
д)
.
е)
ж)
.
з)
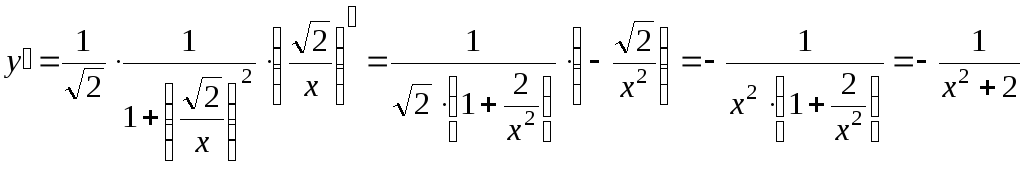
и)
Для упрощения дифференцирования, немного преобразуем функцию:
.
Получаем:
.
Производная обратной функции
Пусть
функции
и
– взаимно-обратные. Тогда
если
,
,
то:
,
.
Пример 11.
Найти
производную
функции 
.
Решение.
,
тогда
.
Дифференцирование функций, заданных параметрически
Если
функция
от независимой переменной
задана посредством вспомогательной
переменной (параметра)
:
,
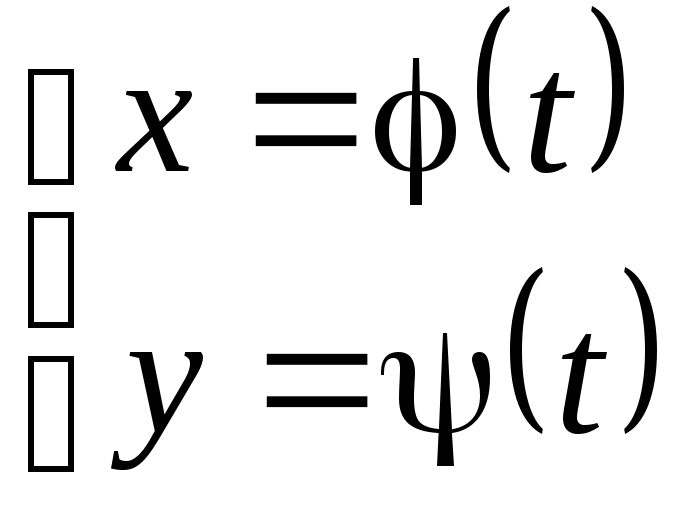то говорят, что функция задана
параметрически и производная
определяется по формуле:
.
Пример 12.
Найти
производную
,
функции
.
Решение.
Находим
производные
и
от переменной
:
;
;
Тогда:
.
Дифференцирование неявной функции
Если
зависимость между
и
задана в неявном виде уравнением
,
то производная
определяется
следующим образом:
дифференцируются обе части уравнения, рассматривая при этом
,
как функцию аргумента
;полученное уравнение решается относительно
.
В результате получается выражение производной от неявной функции в виде:
.
Пример 13.
Найти
производную функции
.
Решение.
Дифференцируем
обе части уравнения и выражаем
:
; 
;
; 
;
; 
;
; 
.
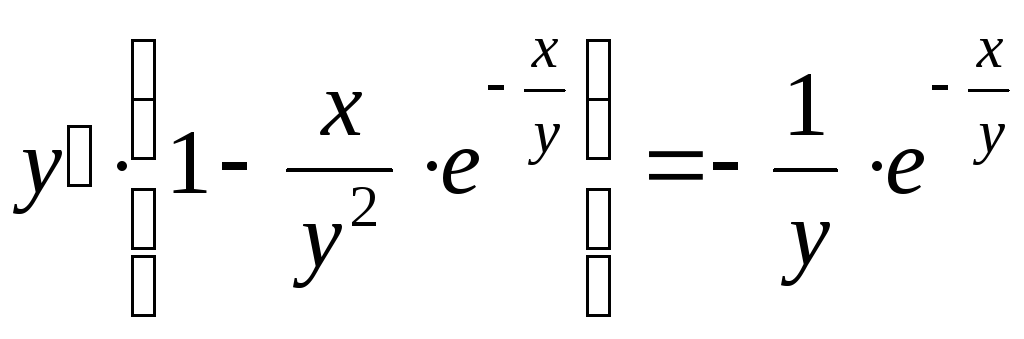Чтобы
избавиться от многоэтажной дроби в
ответе, домножим числитель и знаменатель
получившейся дроби на выражение
.
.