Логарифмическое дифференцирование

При вычислении производной от логарифма произведения, частного, степени или корня, для упрощения нахождения производной проводят предварительное преобразование (см. Пример 10(и)).

В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать (по умолчанию имеется в виду натуральный логарифм). Затем найти производную от этого логарифма и по ней отыскать производную от заданной функции. Такой прием называется логарифмическим дифференцированием.

Метод логарифмического дифференцирования позволяет легко найти производную показательно-степенной функции вида

,

где и – дифференцируемые функции аргумента .

Пример 14.

Найти производную функции .

Решение.

Прологарифмируем обе части функции и преобразуем выражение:

.

Теперь дифференцируем уравнение, как неявно заданную функцию:

;

;

;

;

Так как , то окончательно получаем:

.

Производные высших порядков

Производной 2-го порядка от функции называется производная от её первой производной, т.е.

.

Аналогично, производной 3-го порядка от функции называется производная от её второй производной, т.е.

.

Таким образом, производной -го порядка от функции называется производная от производной -го порядка, т.е.

.

Следовательно, для нахождения производной -го порядка необходимо последовательно найти производную первого, затем второго, затем третьего и т.д. до-го порядка.

Пример 15.

Найти третью производную функции .

Решение.

;

;

.

2.3. Дифференциал функции

Из определения производной и свойств пределов следует, что если

то ,

где – бесконечно малая величина ().

Выражаем и получаем, что:. Так как, то в дальнейшем ее можно не учитывать и мы получим:

Главная часть приращения функции, линейная относительно приращения независимой переменной , называется дифференциалом функции и обозначаетсяили:

.

Т. к. дифференциал , то дифференциал функции равен произведению производной функции на дифференциал аргумента:

.

Таким образом, для нахождения дифференциала функции, необходимо найти производную и умножить её на дифференциал независимой переменной .

Пример 16.

Найти дифференциал функции .

Решение.

.

2.4. Применение дифференциального исчисления функции одной переменной

2.4.1. Применение производной при вычислении пределов.

Правило Лопиталя

При вычислении предела функции подстановка предельного значения аргумента часто приводит к неопределенностям вида ,, от которых невозможно избавиться при помощи ранее изученных приемов. Теорема, известная под названиемправило Лопиталя, является одним из основных инструментов для раскрытия таких неопределенностей.

Правило Лопиталя: Пусть в некоторой окрестности точки функцииидифференцируемы и. Еслииодновременно являются бесконечно малыми или бесконечно большими функциями при , то

,

при условии, что предел отношения производных существует.

Эта теорема справедлива также и для односторонних пределов, и в случае, когда .

В некоторых случаях раскрытие неопределенностей вида может потребовать неоднократного применения правила Лопиталя.

Неопределенности ,,,,, сводятся к неопределенностям вида путем алгебраических преобразований.

Пример 17.

Вычислить с помощью правила Лопиталя пределы:

а); б); в).

Решение.

а)

.

б)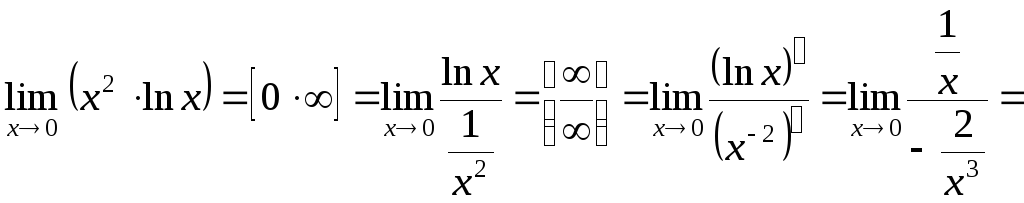

.

в) .

Обозначим искомый предел через и прологарифмируем выражение:

;

или .

Тогда:

.

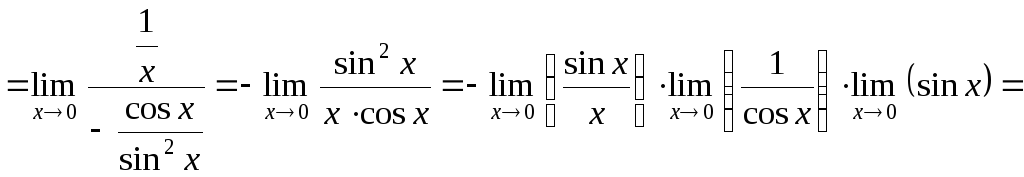
Так как , то искомый предел.