3.1.5. Интегрирование тригонометрических функций.
Рассмотрим основные виды интегралов, подынтегральная функция в которых содержит тригонометрические функции.
I.
Интегралы вида
,
где
и
– целые числа.
Выделим здесь три случая, имеющие важное значение.
1)
Если оба показателя степени
и
– четные неотрицательные числа, то
необходимо преобразовать подынтегральную
функцию с помощью формул понижения
степени:
2)
Если хотя бы один из показателей степени
или
(или и
и
)
нечетное число, то интеграл функции
находят путем отделения от нее одного
множителя и применения формулы:
,
и последующей подстановки:
– если
– нечетное положительное число, то
;
– если
– нечетное положительное число, то
.
3)
Если оба показателя степени
и
– четные и хотя бы одно из них отрицательное,
то применяют замену переменной
или
.
Могут применяться формулы:
.
Пример 29.
Найти интегралы:
а)
;
б)
;
в)
;
г)
.
Решение.
а)
В
данном случае показатели:
– четные положительные числа. Применим
формулу понижения степени:
б)
В
данном случае показатели:
,
– нечетное число. Отделим от нечетной
степени один множитель первой степени,
воспользуемся тождеством
и сделаем подстановку
в)
В
данном случае показатели:
– нечетное число, а
.
Отделим от нечетной степени один
множитель первой степени, воспользуемся
тождеством
и сделаем подстановку
.
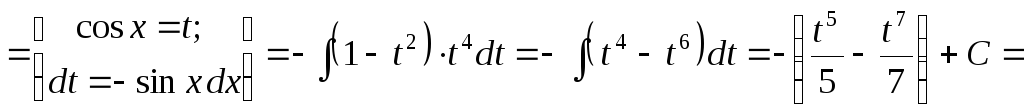
г)
.
В
данном случае показатели:
– четные, но
– отрицательное число. Преобразуем
подынтегральную функцию, воспользуемся
тождеством
и применим
подстановку
.
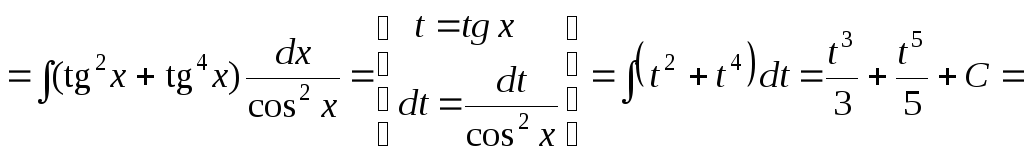
II.
Интегралы вида
гдеR
– рациональная функция от тригонометрических
функций, решаются при помощи универсальной
тригонометрической подстановки:
.
Тогда:
Пример 30.
Найти
интеграл
Решение.
Применяем
универсальную тригонометрическую
подстановку
.
Тогда исходный интеграл принимает вид:
.
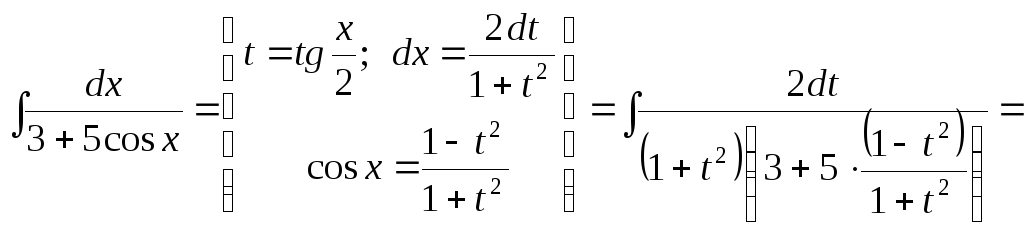
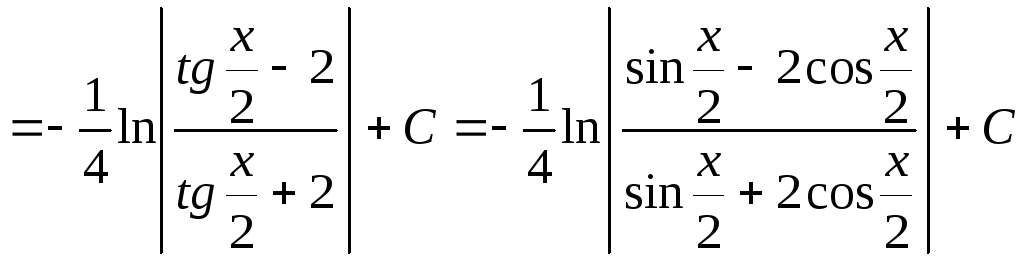В
некоторых случаях нахождение интегралов
вида
может быть упрощено:
– Если
– нечетная функция относительно
,
т.е. если
то применяется подстановка
– Если
– нечетная функция относительно
,
т.е. если
то применяется подстановка
– Если
– четная функция относительно
и
,
т.е. если
,
то применяется подстановка
.
Пример 31.
Найти
интегралы а)
;
б)
.
Решение.
а)
Подынтегральная функция нечетная
относительно
Применяем подстановку
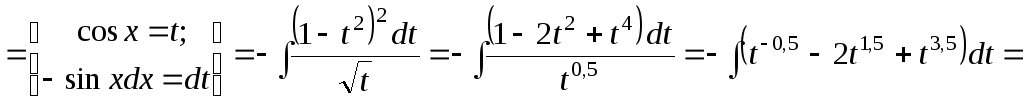
б)
Подынтегральная
функция четная относительно
и
.
Применяем подстановку
и формулу
.
.
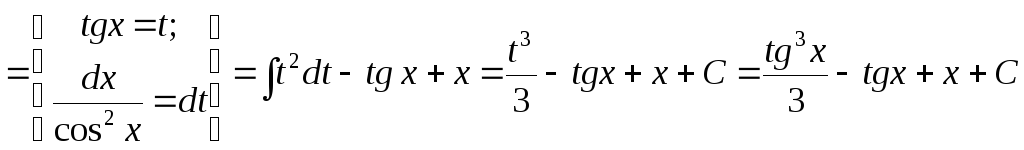III.
Интегралы
вида
,
,
,
где
и
– некоторые числа (коэффициенты).
Подобные интегралы преобразуются в табличные с помощью преобразования произведения тригонометрических функций в сумму по формулам:
, , .
Пример 32.
Найти
интеграл
.
Решение.
.
3.1.6. Интегрирование некоторых видов иррациональных функций
В некоторых случаях интегралы от иррациональных функций с помощью соответствующей подстановки сводят к интегралам от рациональных функций.
І.
Интегралы вида:
,
где
– рациональная функция.
Такие
интегралы вычисляют с помощью подстановки
,
где
– общий знаменатель дробей
(
– наименьшее общее кратное чисел
и
).
Пример 33.
Найти
интеграл
.
Решение.
.
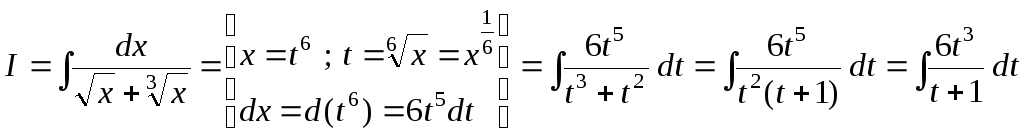Мы получили интеграл от неправильной рациональной дроби. Разделим числитель на знаменатель.
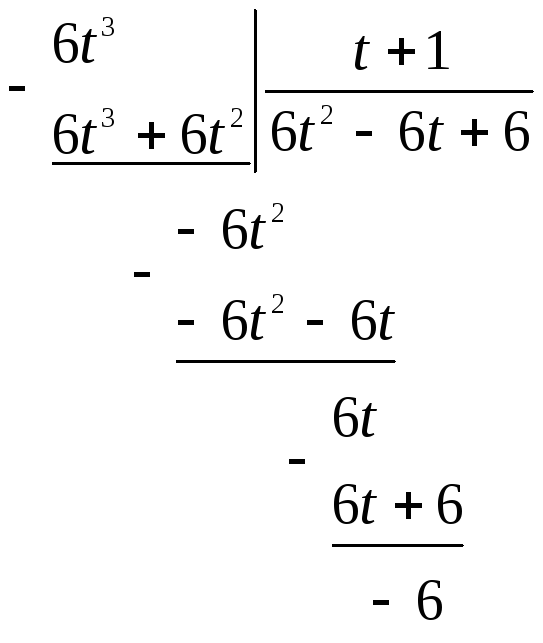
Тогда интеграл примет вид:
ІІ.
Интегралы вида
вычисляют с помощью подстановки
,
где
– наименьшее общее кратное чисел
.
Пример 34.
Найти
интеграл
.
Решение.
.
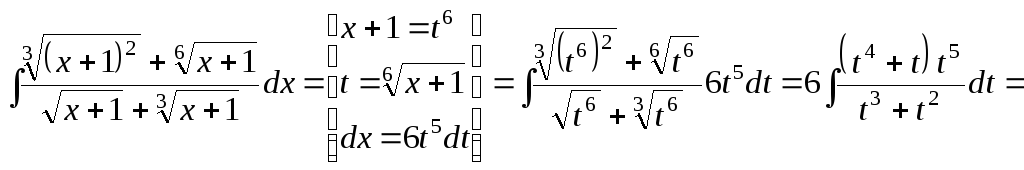
ІІІ.
Интегралы вида
,
,
вычисляют выделением полного квадрата
под знаком радикала и заменой переменной.
В качестве новой переменной принимается
выражение, которое находится в скобке
в квадрате, получившейся после выделения
полного квадрата.
Пример 35.
Найти
интеграл
.
Решение.
Выделим полный квадрат в выражении под знаком радикала:
.
После
выделение полного квадрата видно, что
в качестве новой переменной интегрирования
следует выбрать выражение 
.
Получаем:
.
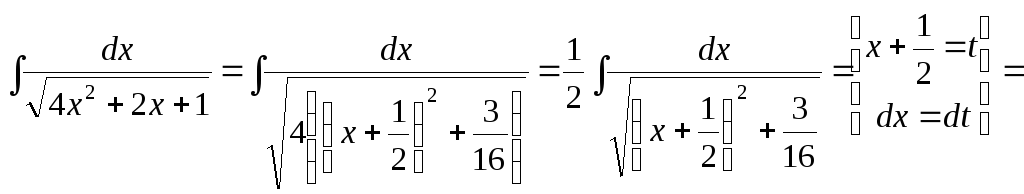
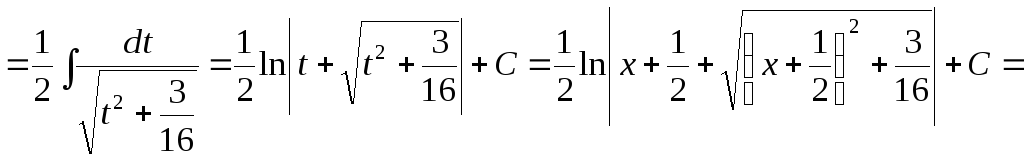
ІV.
Интегралы вида
,
,
приводятся к интегралам от функций,
рационально зависящих от тригонометрических
функций, с помощью следующих
тригонометрических подстановок:
для
интеграла
:
,
тогда
;
для
интеграла
:
,
тогда
для
интеграла
:
,
тогда
Пример 36.
Найти
интегралы: а)
;
б)
.
Решение.
а)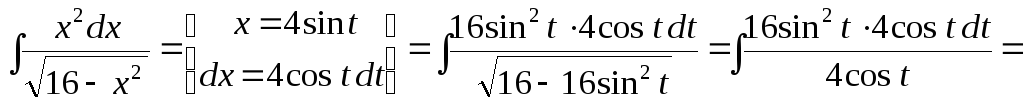
.
Вернемся
к старой переменной и получим ответ в
наиболее простом виде. Так как
,
то
; 
;
.
Следовательно, окончательный ответ имеет вид:
.
б)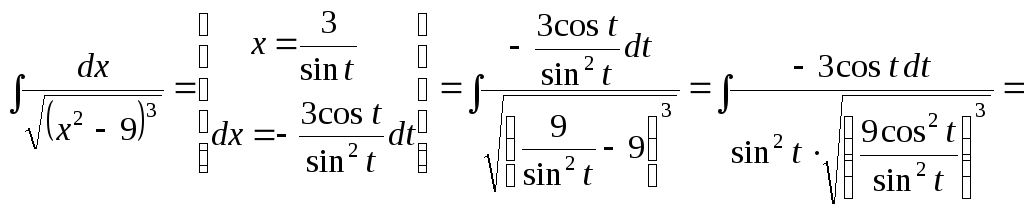
.
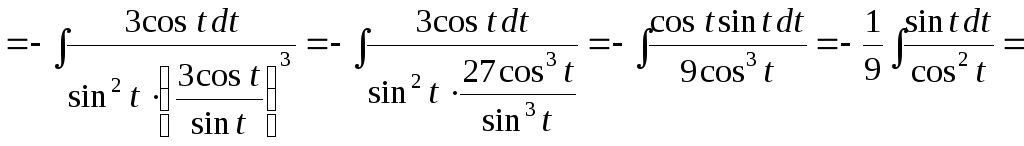
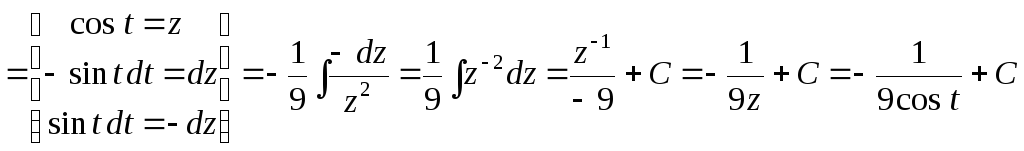Вернемся
к старой переменной и получим ответ в
наиболее простом виде. Так как
,
то
.
Следовательно, окончательный ответ имеет вид:
.
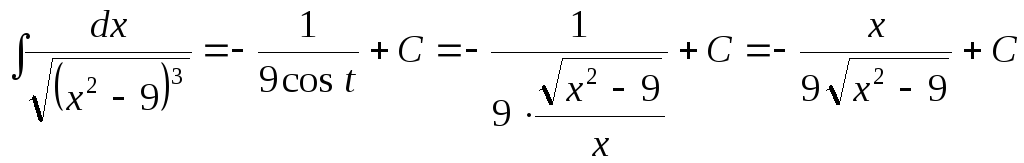