2.4.2. Возрастание и убывание функции на интервале

Функция называется возрастающей на интервале , если большему значению аргумента из этого интервала соответствует большее значение функции, т.е. при, где и – любые две точки из интервала верно неравенство .

Если большему значению аргумента из этого интервала соответствует меньшее значение функции, т.е. при верно неравенство ,то функция называется убывающей на интервале .

Возрастание и убывание функции на интервале тесно связано со знаком производной функции в точках этого интервала.

Необходимые условия возрастания и убывания функции:

Если дифференцируемая функция на интервале возрастает (убывает), то её производная на этом интервале неотрицательная (неположительная), т.е.().

Достаточные условия возрастания и убывания функции:

Если непрерывная на отрезке функция в каждой точке отрезка имеет положительную (отрицательную) производную, то она возрастает (убывает) на этом отрезке.

Интервалы, в которых функция является только возрастающей или только убывающей, называются интервалами монотонности.

Эти интервалы ограничены критическими точками І рода – значениями аргумента, в которых производная функции равна нулю или не существует.

Для нахождения интервалов монотонности, необходимо нанести на числовую ось граничные точки области определения и все критические точки функции. Числовая ось при этом разбивается на некоторое число интервалов, на каждом из которых производная не меняет знак. Для того чтобы узнать возрастает или убывает функция на данном интервале, достаточно выяснить какой знак имеет производная в произвольной точке этого интервала. Если в этой точке , то функция возрастает на данном интервале, если – то функция убывает на данном интервале.

2.4.3. Экстремумы функции

Точка называется точкой максимума функции , если существует такая окрестность точки , что для всех точек этой окрестности выполняется неравенство.

Значение функции в точке максимума называетсямаксимумом функции.

Точка называется точкой минимума функции ,если существует такая окрестность точки , что для всех точек этой окрестности выполняется неравенство.

Значение функции в точке минимума называетсяминимумом функции.

Максимум и минимум объединяются под общим названием экстремум функции, а точки максимума и минимума называются точками экстремума.

Функция на всей области определенияможет иметь несколько точек экстремума. Это означает, что понятие максимума и минимума функции носят локальный характер. Это наибольшее и наименьшее значение функции только в окрестности рассматриваемой точки, а не во всей области её определения.

Необходимое условие существования экстремума функции:

Если непрерывная функция в точке имеет экстремум, то её производная в этой точке равна нулю или не существует, т.е. точка экстремума является критической точкой І рода.

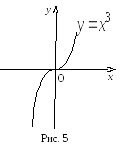
Замечание: Не во всякой критической точке функция имеет экстремум.

Так, например, для функции (график функции показан на рис. 5) производная. Производная существует при любом значении аргумента и равна нулю при , т.е. функция имеет одну критическую точку І рода: .Однако в данной критической точке экстремума нет.

SHAPE \* MERGEFORMAT

Чтобы проверить, имеет ли функция в критической точке экстремум, необходимо дополнительное исследование. Для этого используют достаточные условия существования экстремума.

Первое достаточное условие существования экстремума.

Если непрерывная функция имеет производную во всех точках интервала, содержащего критическую точку , (за исключением, может быть, самой этой точки) и производная при переходе через точку слева направо меняет знак с плюса на минус, то функция в этой точке имеет максимум, а если меняет знак с минуса на плюс – минимум.

Второе достаточное условие существования экстремума.

Если в точке первая производная равна нулю , а вторая производная существует и не равна нулю , то при функция в этой точке имеет максимум, а при функция имеет минимум.

Замечание: В тех случаях, когда в критической точке вторая производная равна нулю или не существует, то второй достаточный признак существования экстремума неприменим.

Схема исследования функции на монотонность и экстремум

1. Найти область определения функции .

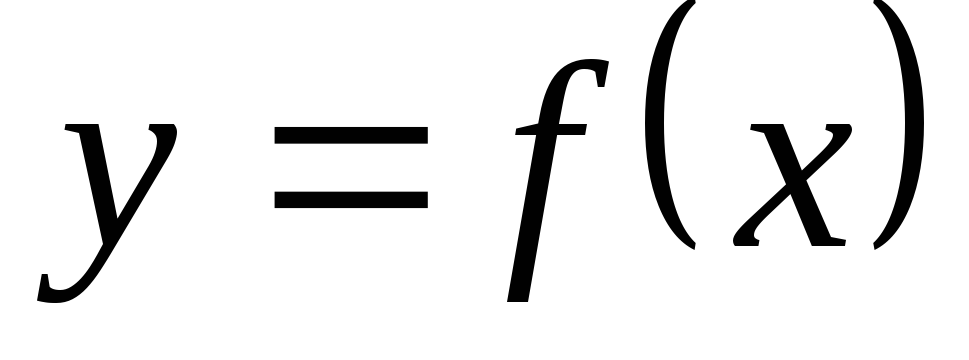2. Найти первую производную .

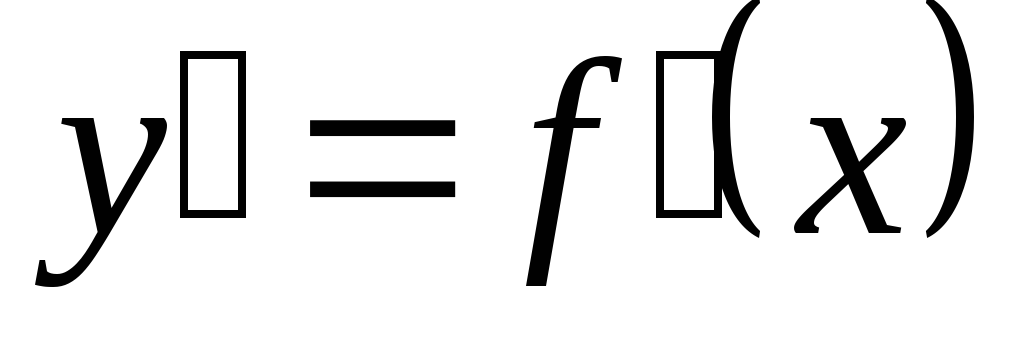3. Найти критические точки І рода.

4. Разбить область определения функции 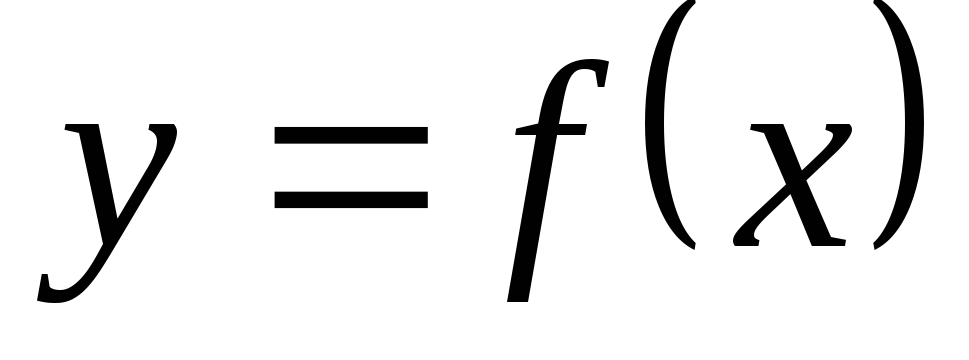критическими точками на интервалы.

5. Определить знак производной на полученных интервалах (методом подстановки значений аргумента или методом интервалов).

6. Сделать вывод об интервалах монотонности.

7. Определить, используя первый достаточный признак экстремума, какие из критических точек являются точками экстремума.

8. Вычислить значение функции в полученных точках экстремума.

9. Результаты оформить в виде таблицы.

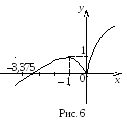
Пример 18.

Найти интервалы монотонности и точки экстремума функции .

Решение.

Функция определена на всей числовой оси. Область определения функции имеет вид: .

Найдем первую производную функции:

.

Найдем критические точки первого рода:

.

Дробь равна нулю, если числитель равен нулю и знаменатель не равен нулю:

; ;.

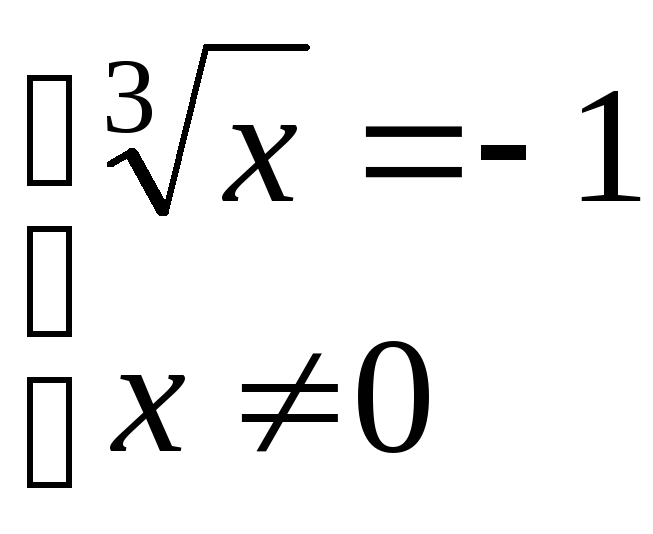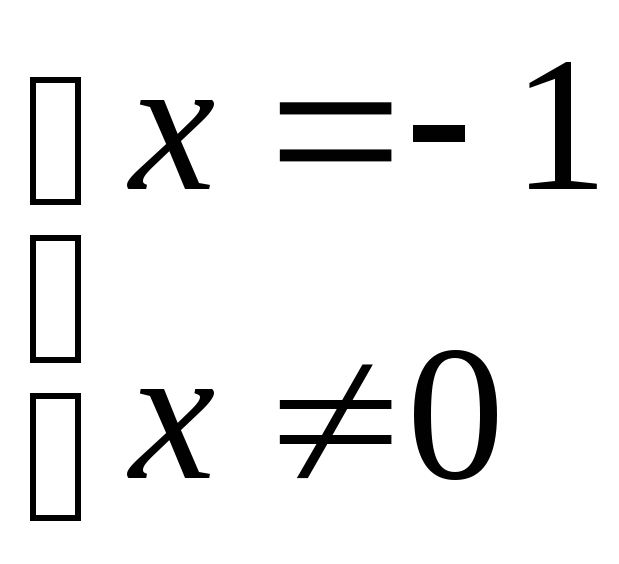Следовательно, точки и – критические точки І рода.

Разбиваем всю числовую ось на интервалы и определяем знак производной на каждом интервале.

		– 1		0
	+	0	–	не сущ.	+
	↗	1	↘	0	↗

max min

Так как на интервалах производная положительная значит, на этих интервалах функция возрастает.

Так как на интервале производная отрицательная значит, на этом интервале функция убывает.

Так как при переходе через критическую точку производная меняет знак с «+» на «–», то в этой точке функция имеет максимум.

Так как при переходе через критическую точку производная меняет знак с «–» на «+», то в этой точке – минимум функции.

Определим значения функции в критических точках.

;

.

Приближенный вид графика функции показан на рис 6.