Метод интегрирования по частям

Метод интегрирования по частям применяется, в основном, когда подынтегральная функция состоит из произведения двух сомножителей определенного вида. Формула интегрирования по частям имеет вид:

.

Она дает возможность свести вычисление заданного интеграла к вычислению интеграла, который оказывается более простым, чем данный.

Большую часть интегралов, вычисляемых методом интегрирования по частям, можно разбить на три группы:

1. Интегралы вида ,,, где– многочлен,– число, не равное нулю

В этом случае через обозначают многочлен, а всю остальную часть подынтегрального выражения через.

2. Интегралы вида ,,,,, где– многочлен.

В этом случае через обозначают, а всю остальную часть подынтегрального выражения через:

3. Интегралы вида ,, где– числа.

В этом случае через обозначаюти применяют формулу интегрирования по частям дважды, возвращаясь в результате к исходному интегралу, после чего исходный интеграл выражается из равенства.

Замечание: В некоторых случаях для нахождения заданного интеграла формулу интегрирования по частям необходимо применять несколько раз. Также метод интегрирования по частям комбинируют с другими методами.

Пример 26.

Найти интегралы методом по частям: а) ; б).

Решение.

а)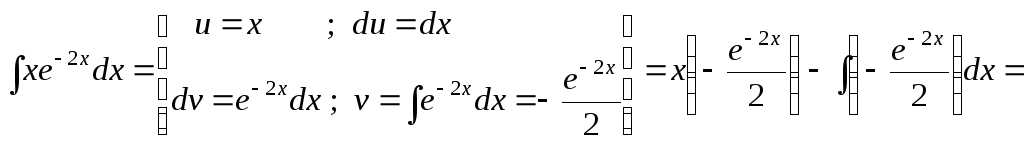

.

б)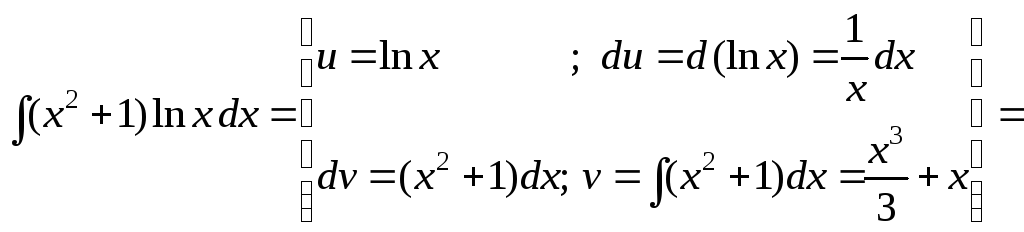

.

3.1.4. Интегрирование дробно-рациональных функций

Дробно-рациональной функцией (рациональной дробью) называется функция, равная отношению двух многочленов: , где– многочлен степени,– многочлен степени .

Рациональная дробь называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе, т.е. , в противном случае (если ) рациональная дробь называется неправильной.

Любую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби, разделив числитель на знаменатель по правилу деления многочленов:

,

где – целая часть от деления,– правильная рациональная дробь,– остаток от деления.

Правильные рациональные дроби вида:

I. ;

II. ;

III. ;

IV. ,

где ,,,,,, – действительные числа и (т.е. квадратный трехчлен в знаменателеIII и IV дробей не имеет корней – дискриминант отрицательный) называются простейшими рациональными дробями I, II, III и IV типов.

Интегрирование простейших дробей

Интегралы от простейших дробей четырех типов вычисляются следующим образом.

I) .

II) ,.

III) Для интегрирования простейшей дроби III типа в знаменателе выделяют полный квадрат, производят замену . Интеграл после подстановки разбивают на два интеграла. Первый интеграл вычисляют выделением в числителе производной знаменателя, что дает табличный интеграл, а второй интеграл преобразовывают к виду, так как, что также дает табличный интеграл.

;

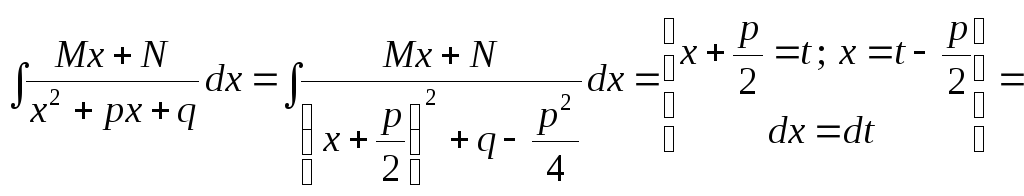
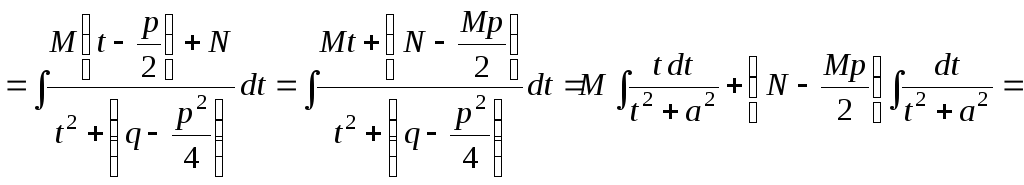
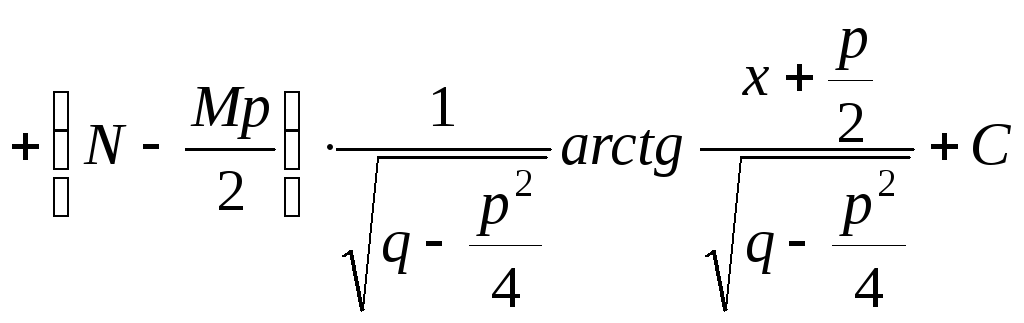IV) Для интегрирования простейшей дроби IV типа в знаменателе выделяют полный квадрат, производят замену . Интеграл после подстановки разбивают на два интеграла. Первый интеграл вычисляют подстановкой, а второй с помощью рекуррентных соотношений.

Пример 27.

Найти интегралы от простейших дробей:

а); б); в).

Решение.

а) .

б) .

в)

.

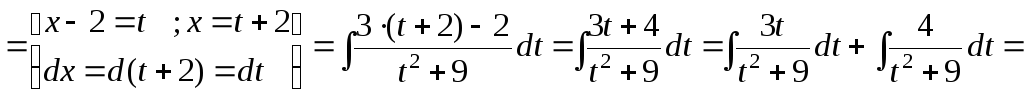
Всякую правильную рациональную дробь, знаменатель которой может быть разложен на множители, можно представить в виде суммы простейших дробей. Разложение на сумму простейших дробей осуществляют методом неопределенных коэффициентов. Он заключается в следующем:

– каждому множителю знаменателя соответствует одна дробь вида;

– каждому множителю знаменателя соответствует сумма дробей вида

;

– каждому квадратному множителю знаменателя соответствует дробь вида;

– каждому квадратному множителю знаменателя соответствует суммадробей вида

,

где – неопределенные коэффициенты.

Для нахождения неопределенных коэффициентов правую часть в виде суммы простейших дробей приводят к общему знаменателю и преобразовывают. В результате получается дробь с тем же знаменателем, что и в левой части равенства. Затем отбрасывают знаменатели и приравнивают числители. В результате получается тождественное равенство, в котором левая часть – многочлен с известными коэффициентами, а правая часть – многочлен с неопределенными коэффициентами.

Существует два способа определения неизвестных коэффициентов: метод неопределенных коэффициентов и метод частных значений.

Метод неопределенных коэффициентов.

Т.к. многочлены тождественно равны, то равны коэффициенты при одинаковых степенях . Приравнивая коэффициенты при одинаковых степеняхв многочленах левой и правой частей, получим систему линейных уравнений. Решая систему, определяем неопределенные коэффициенты.

Метод частных значений.

Т.к. многочлены тождественно равны, то, подставляя вместо в левую и правую части любое число, получим верное равенство, линейное относительно неизвестных коэффициентов. Подставляя столько значений, сколько неизвестных коэффициентов, получим систему линейных уравнений. Вместов левую и правую части можно подставлять любые числа, однако более удобно подставлять корни знаменателей дробей.

После нахождения значений неизвестных коэффициентов, исходная дробь записывается в виде суммы простейших дробей в подынтегральное выражение и осуществляется ранее рассмотренное интегрирование по каждой простейшей дроби.

Схема интегрирования рациональных дробей:

1. Если подынтегральная дробь неправильная, то необходимо представить ее в виде суммы многочлена и правильной рациональной дроби (т.е. разделить многочлен числителя на многочлен знаменателя с остатком). Если подынтегральная дробь правильная сразу переходим ко второму пункту схемы.

2. Разложить знаменатель правильной рациональной дроби на множители, если это возможно.

3. Разложить правильную рациональную дробь на сумму простейших рациональных дробей, используя метод неопределенных коэффициентов.

4. Проинтегрировать полученную сумму многочлена и простейших дробей.

Пример 28.

Найти интегралы от рациональных дробей:

а) ; б); в).

Решение.

а) .

Т.к. подынтегральная функция неправильная рациональная дробь, то выделим целую часть, т.е. представим ее в виде суммы многочлена и правильной рациональной дроби. Разделим многочлен в числителе на многочлен в знаменателе уголком.

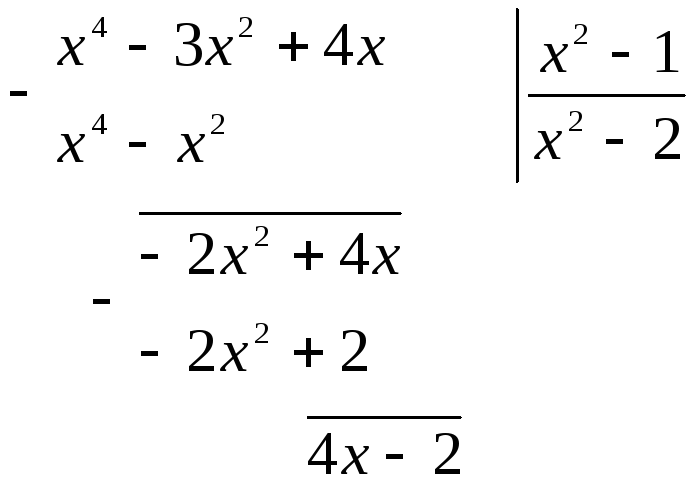
Исходный интеграл примет вид: .

Разложим правильную рациональную дробь на сумму простейших дробей c помощью метода неопределенных коэффициентов:

.

Отбросим знаменатели и приравняем левую и правую части:

.

Приравнивая коэффициенты при одинаковых степенях , получаем:

Решая систему линейных уравнений, получим значения неопределенных коэффициентов: А = 1; В = 3.

Тогда искомое разложение имеет вид: .

Найдем исходный интеграл, учитывая полученное разложение:

=.

б) .

Разложим подынтегральную функцию (правильную рациональную дробь) на сумму простейших дробей с помощью метода неопределенных коэффициентов. Разложение ищем в виде:

.

Приведя к общему знаменателю, получим:

Отбросим знаменатели и приравняем левую и правую части:

.

Приравнивая коэффициенты при одинаковых степенях , получаем систему:

Решая систему из пяти линейных уравнений, находим неопределенные коэффициенты:

.

Тогда искомое разложение имеет вид:

.

Найдем исходный интеграл, учитывая полученное разложение:

.

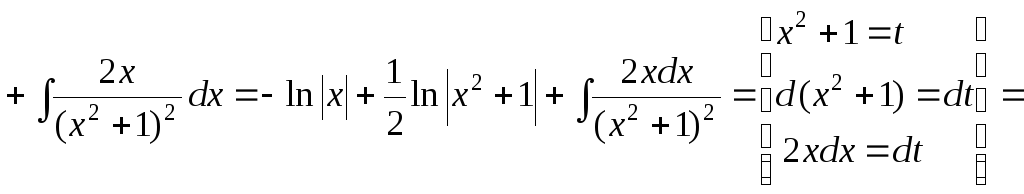
в) .

Разложим подынтегральную функцию (правильную рациональную дробь) на сумму простейших дробей с помощью метода неопределенных коэффициентов. Разложение ищем в виде:

.

Приведя к общему знаменателю, получим:

.

Отбросим знаменатели и приравняем левую и правую части:

.

Для нахождения неопределенных коэффициентов применим метод частных значений. Придадим частные значения , при которых множители обращаются в нуль, т. е. подставим эти значения в последнее выражение и получим три уравнения:

; ;

; ;

; .

Тогда искомое разложение имеет вид:

.

Найдем исходный интеграл, учитывая полученное разложение: