3.2.2. Свойства определенного интеграла

1. Постоянный множитель можно выносить за знак интеграла:

, где .

2. Интеграл от алгебраической суммы интегрируемых функций равен алгебраической сумме интегралов от этих функций:

.

3. При перестановке пределов интегрирования определенный интеграл меняет свой знак на противоположный:

.

Замечание. Если пределы интегрирования равны между собой , то

.

4. Интеграл по всему отрезку равен сумме интегралов по частям этого отрезка:

,

5. Значение определенного интеграла не зависит от обозначения переменной интегрирования, т.е:

.

6. «Теорема о среднем»: Если функция непрерывна на отрезке , то существует точка такая, что

.

7. Неравенство между непрерывными на отрезке функциями можно интегрировать. Так, если при, то

.

8. Интеграл можно оценить наименьшим значением функции и наибольшим значением функциина отрезке :

.

3.2.3. Вычисление определенного интеграла

При вычислении определенных интегралов применяют те же методы, что и для неопределенных интегралов, а именно: непосредственное интегрирование, метод замены переменной (метод подстановки) и метод интегрирования по частям.

Метод замены переменной в определенном интеграле

Если для непрерывной подынтегральной функции невозможно найти первообразнуюнепосредственным интегрированием, то для вычисления определенного интегралаприменяют замену переменной. В результате интеграл приводится к табличному и вычисляется по формуле Ньютона-Лейбница. Пределы интегрирования изменяются в соответствие с выбранной подстановкой.

Если функция и ее производная непрерывны на отрезке и при этом ,, то справедливо равенство:

.

Данная формула описывает метод подстановки в определенном интеграле.

Замечание: При вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется, т.к. пределы интегрирования в определенном интеграле изменяются с учетом новой переменной.

Пример 39.

Вычислить определенные интегралы методом подстановки:

а) ;б) ; в).

Решение.

а)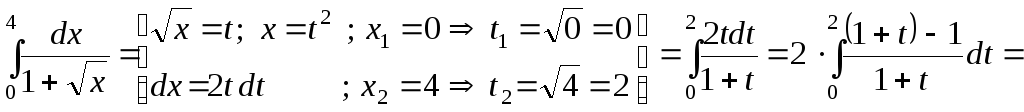

.

б)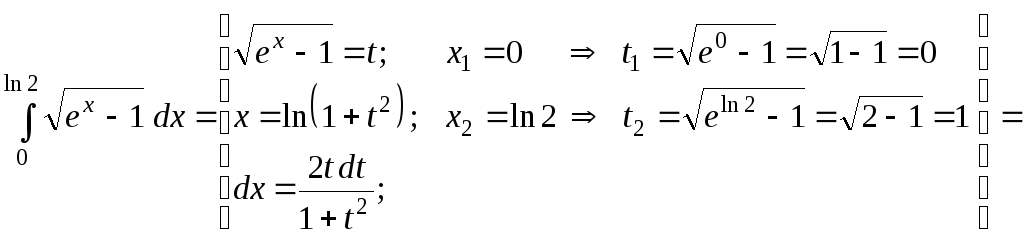

.

в)

.

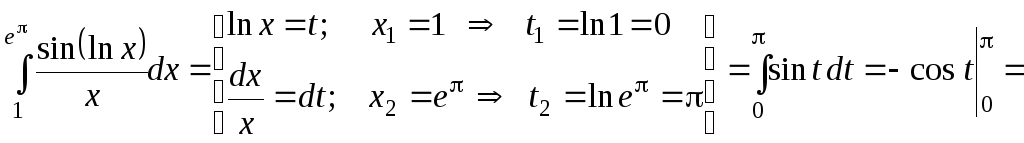
Метод интегрирования по частям в определенном интеграле

Если функции иимеют непрерывные производные на отрезке , то формула интегрирования по частям имеет вид:

.

Пример 40.

Вычислить определенные интегралы методом интегрирования по частям:

а) ; б).

Решение.

а)

.

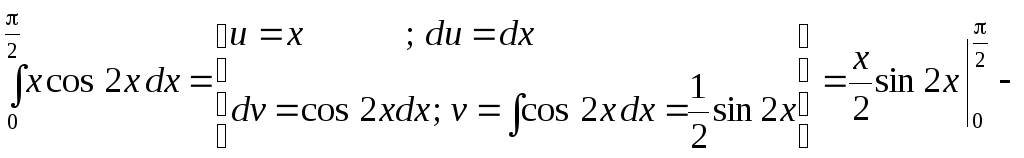
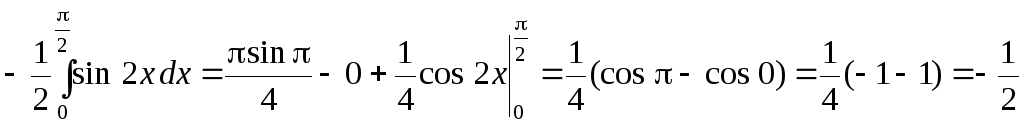б)

.

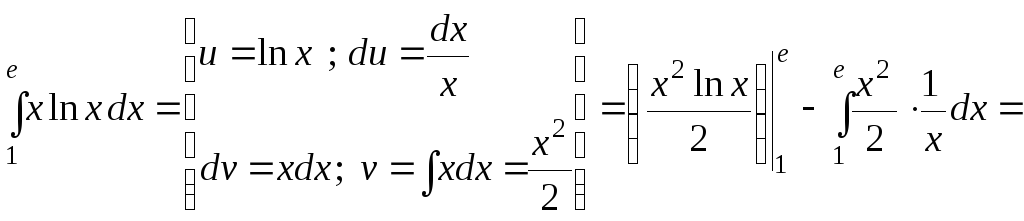
3.2.4. Несобственные интегралы

Определенный интеграл , в котором промежуток интегрирования– конечный, а подынтегральная функция– непрерывна на отрезке , называетсясобственным интегралом.

Несобственным интегралом называется определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв. Соответственно, различают несобственные интегралы I рода (с бесконечными пределами) и II рода (интеграл от разрывной функции).

Несобственным интегралом первого рода непрерывной на интервалефункцииназывается конечный предел.

Таким образом, по определению:

.

Если предел, стоящий в правой части равенства существует и конечен, то несобственный интеграл сходится, в противном случае – расходится.

Аналогично определяется несобственный интеграл на интервале :

.

Несобственный интеграл с двумя бесконечными пределами (на интервале ) разбивается на два по формуле:

, где – произвольное число.

Такой интеграл сходится лишь тогда, когда сходятся оба интеграла на которые он разбивается.

Пример 41.

Вычислить несобственные интегралы І рода: а) ; б).

Решение.

а) .

Так как предел – конечный, то несобственный интеграл сходится.

б) .

Так как предел – бесконечный, то несобственный интеграл расходится.

Несобственным интегралом второго рода непрерывной на интервалефункции, имеющей бесконечный разрыв при, называется конечный предел. Таким образом, по определению:

.

Если предел, стоящий в правой части равенства существует и конечен, то несобственный интеграл сходится, в противном случае – расходится.

Аналогично, если функция , непрерывная на интервале, имеет бесконечный разрыв при, то несобственный интеграл второго рода определяется по формуле:

.

Если функция имеет бесконечный разрыв во внутренней точкеотрезка, то несобственный интеграл второго рода определяется по формуле:

.

Такой интеграл сходится лишь тогда, когда сходятся оба интеграла на которые он разбивается.

Пример 42.

Вычислить несобственный интеграл ІІ рода .

Решение.

Подынтегральная функция имеет бесконечный разрыв на левой границе промежутка интегрирования , так как данная функция не определена прии. Следовательно:

.

Так как предел – бесконечный, то несобственный интеграл расходится.