
- •Высшая математика математический анализ функций одной переменной
- •0501 „Экономика и предпринимательство”,
- •0502 „Менеджмент”
- •Издание рассмотрено и рекомендовано к печати на заседании кафедры физико-математических дисциплин (протокол № 5 от 13 января 2009 г.);
- •Содержание
- •Краткие теоретические сведения
- •1. Пределы и непрерывность функции
- •1.1. Предел числовой последовательности и функции в точке и на бесконечности. Односторонние пределы функции в точке.
- •1.2. Основные теоремы о пределах
- •1.3. Бесконечно малые и бесконечно большие функции
- •1.4. Примеры вычисление пределов
- •1.5. Непрерывность функции
- •Вопросы для самоконтроля
- •2. Дифференциальное исчисление функции одной переменной
- •2.1. Производная функции. Геометрический смысл производной функции
- •2.2. Общие правила дифференцирования функции.
- •Основные правила дифференцирования
- •Производная сложной функции
- •Сводная таблица формул дифференцирования
- •Производная обратной функции
- •Дифференцирование функций, заданных параметрически
- •Дифференцирование неявной функции
- •Логарифмическое дифференцирование
- •Производные высших порядков
- •2.3. Дифференциал функции
- •2.4. Применение дифференциального исчисления функции одной переменной
- •2.4.1. Применение производной при вычислении пределов.
- •Правило Лопиталя
- •2.4.2. Возрастание и убывание функции на интервале
- •2.4.3. Экстремумы функции
- •2.4.4. Наибольшее и наименьшее значения функции на отрезке.
- •Значений функции на отрезке:
- •2.4.5. Выпуклость графика функции. Точки перегиба
- •Интервалы выпуклости, вогнутости и точки перегиба:
- •2.4.6. Асимптоты графика функции
- •2.4.7. Полное исследование функции и построения ее графика.
- •2.5. Вопросы для самоконтроля
- •3. Интегральное исчисление функции одной переменной
- •3.1. Неопределенный интеграл
- •3.1.1 Свойства неопределённого интеграла.
- •3.1.2. Таблица неопределенных интегралов
- •3.1.3. Основные методы интегрирования
- •Метод непосредственного интегрирования
- •Метод замены переменной
- •Метод интегрирования по частям
- •3.1.4. Интегрирование дробно-рациональных функций
- •Интегрирование простейших дробей
- •3.1.5. Интегрирование тригонометрических функций.
- •, , .
- •3.1.6. Интегрирование некоторых видов иррациональных функций
- •3.1.7. Интегрирование дифференциального бинома
- •3.1.8. Интегралы, не выражающиеся через элементарные функции
- •3.1.9. Вопросы для самоконтроля
- •3.2. Определенный интеграл
- •3.2.1. Интегральная сумма и определенный интеграл
- •3.2.2. Свойства определенного интеграла
- •3.2.3. Вычисление определенного интеграла
- •Метод замены переменной в определенном интеграле
- •Метод интегрирования по частям в определенном интеграле
- •3.2.4. Несобственные интегралы
- •3.2.5. Геометрические приложения определенного интеграла
- •Вычисление площадей плоских фигур в декартовых координатах
- •Вычисление объема тела вращения
- •Вычисление длины дуги кривой
- •3.2.6. Вопросы для самоконтроля
- •Литература
- •Индивидуальные задания для расчетно-графической работы
- •4) ; 5).
- •Таблицы выбора вариантов заданий для ргр № 2
- •211 Группа
- •212 Группа
- •213 Группа
- •214 Группа
- •215 Группа
- •311 Группа
- •312 Группа
- •313 Группа
- •314 Группа
- •315 Группа
- •316 Группа
- •1111 Группа
- •1112 Группа
- •1211 Группа
- •1212 Группа
- •1311 Группа
- •1312 Группа
- •1313 Группа
- •1511 Группа
- •1512 Группа
1.3. Бесконечно малые и бесконечно большие функции
Функция
![]() называетсябесконечно
малой при
называетсябесконечно
малой при
![]() ,
если
,
если
![]() .
.
По
определению предела функции равенство
![]() означает, что для заданного сколь угодно
малого числа
означает, что для заданного сколь угодно
малого числа
![]() найдётся такое число
найдётся такое число![]() ,
что для всех
,
что для всех![]() удовлетворяющих неравенству
удовлетворяющих неравенству![]() будет выполнятся неравенство
будет выполнятся неравенство![]() .
.
Функция
![]() называетсябесконечно
большой при
называетсябесконечно
большой при
![]() ,
если
,
если
![]() .
.
По
определению предела функции равенство
![]() означает, что для заданного сколь угодно
большого числа
означает, что для заданного сколь угодно
большого числа
![]() найдётся такое число
найдётся такое число
![]() ,
что для всех
,
что для всех![]() удовлетворяющих неравенству
удовлетворяющих неравенству![]() будет выполняться неравенство
будет выполняться неравенство![]() .
.
Замечание:
Аналогично, можно говорить о бесконечно
больших и бесконечно малых функциях
при
![]() .
.
Бесконечно большие и бесконечно малые функции обладают следующими свойствами.
Свойство 1. Сумма конечного числа бесконечно малых функций является функцией бесконечно малой.
Свойство 2. Произведение ограниченной функции на бесконечно малую функцию является функцией бесконечно малой.
Свойство 3. Произведение постоянной на бесконечно малую функцию является функцией бесконечно малой.
Свойство 4. Произведение конечного числа бесконечно малых функций является функцией бесконечно малой.
Свойство 5. Сумма конечного числа бесконечно больших функций является функцией бесконечно большой.
Свойство 6. Произведение ограниченной функции на бесконечно большую функцию является функцией бесконечно большой.
Свойство 7. Произведение постоянной на бесконечно большую функцию является функцией бесконечно большой.
Свойство 8. Функция, обратная по величине бесконечно большой, является функцией бесконечно малой.
Свойство 9. Функция, обратная по величине бесконечно малой, является функцией бесконечно большой.
Замечание: свойства 8 и 9 отражают связь между бесконечно большой и бесконечно малой функциями.
Если
принять следующие обозначения: бесконечно
малая функция – символ 0, бесконечно
большая функция
– символ ,
постоянная величина – символ
![]() ,
ограниченная функция – символ
,
ограниченная функция – символ![]() ,
то все изложенные свойства можно записать
следующим образом:
,
то все изложенные свойства можно записать
следующим образом:
1.
![]() ;
4.
;
4.![]() ; 7.
; 7.![]() ;
;
2.
![]() ; 5.
; 5.![]() ; 8.
; 8.![]() ;
;
3.
![]() ; 6.
; 6.![]() ; 9.
; 9.![]()
Для
сравнения двух бесконечно малых функций
![]() и
и![]() при
при
![]() находят
предел их отношения:
находят
предел их отношения:
![]()
Если
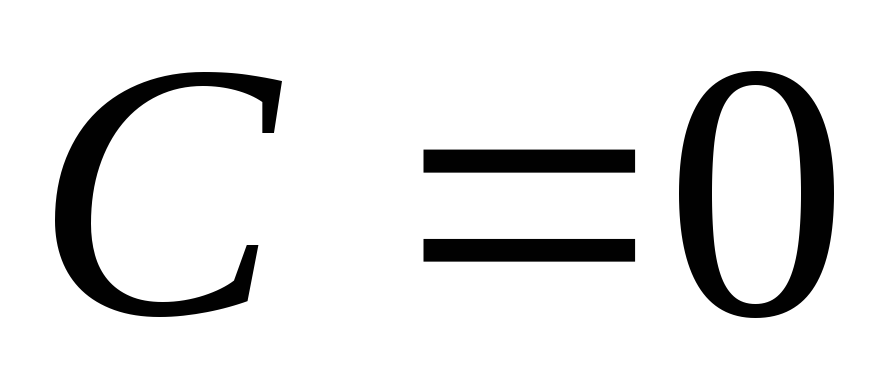 ,
то
,
то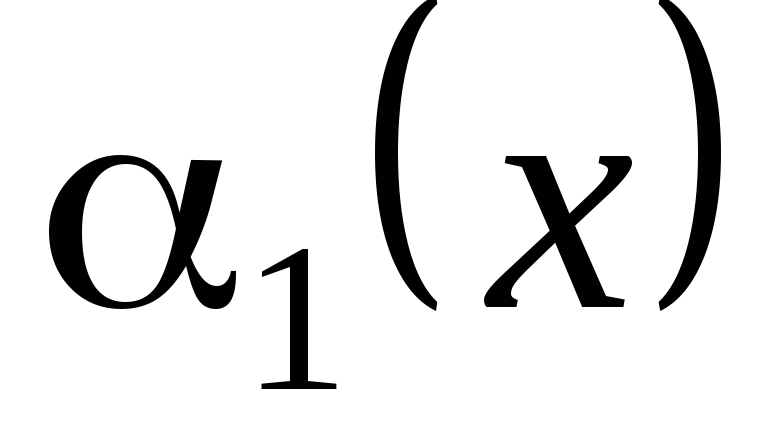 называется бесконечно малой функцией
более высокого порядка по сравнению с
называется бесконечно малой функцией
более высокого порядка по сравнению с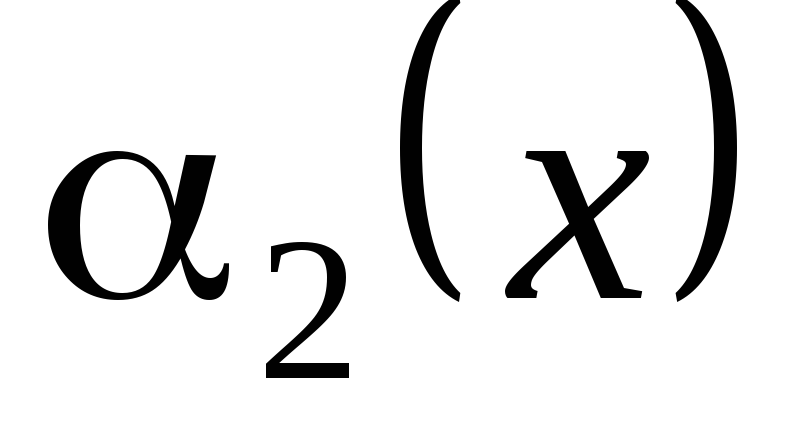 .
.Если
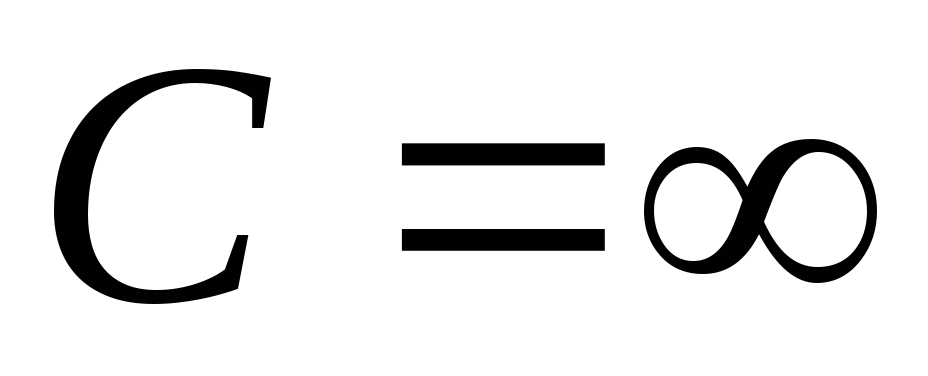 то
то называется бесконечно малой функцией
более высокого порядка по сравнению с
называется бесконечно малой функцией
более высокого порядка по сравнению с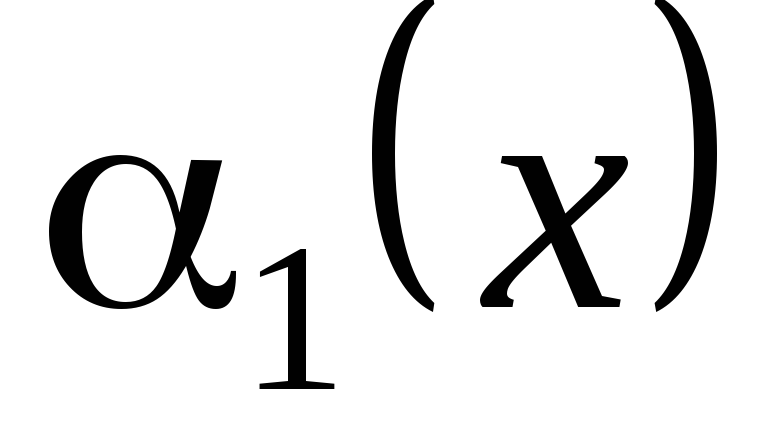 .
.Если
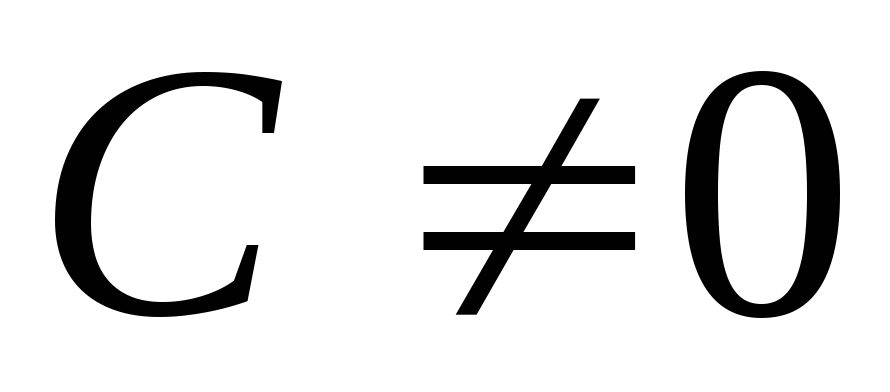 ,
то
,
то и
и называются бесконечно малыми функциями
одного и того же порядка.
называются бесконечно малыми функциями
одного и того же порядка.Если
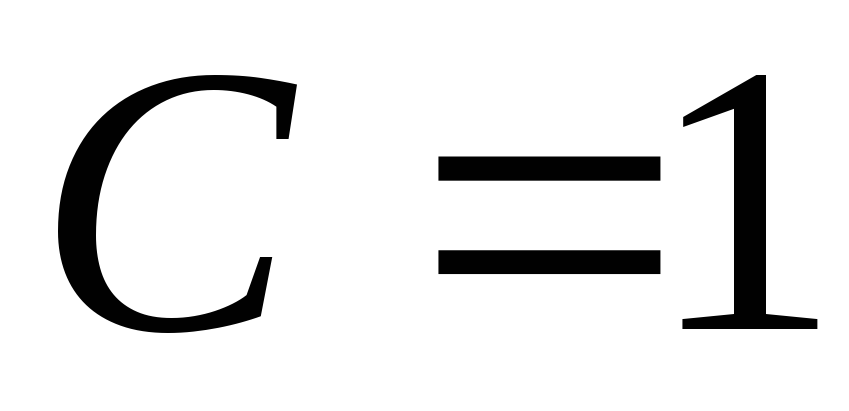 ,
то
,
то
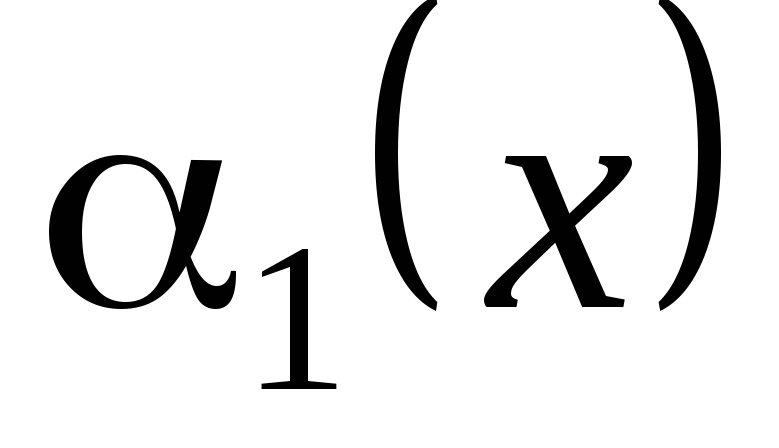 и
и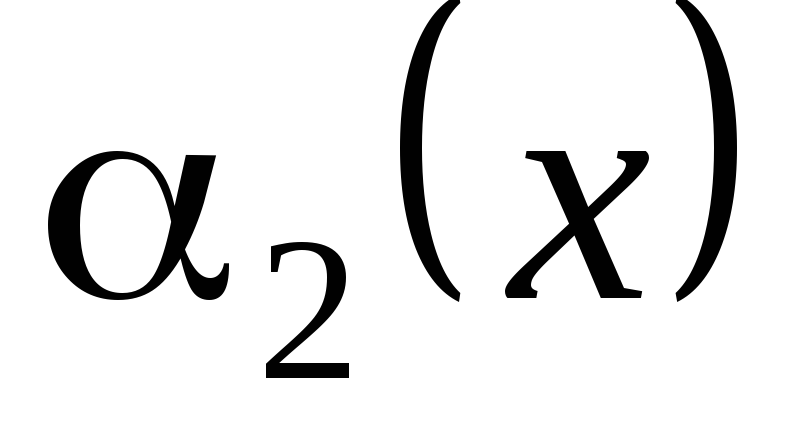 называются эквивалентными (равносильными)
бесконечно малыми:
называются эквивалентными (равносильными)
бесконечно малыми:
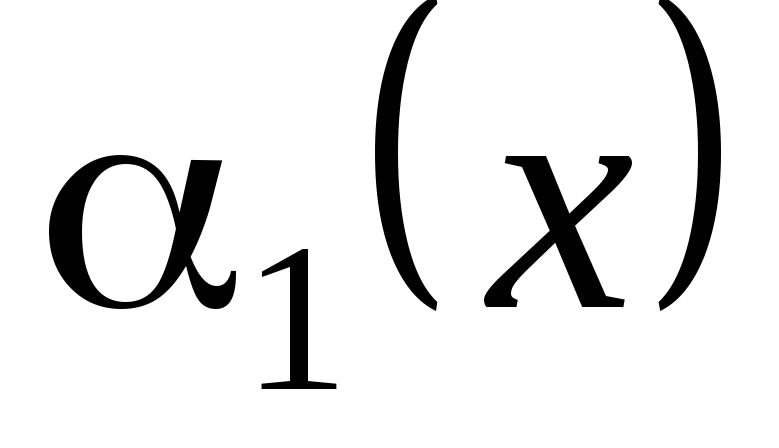
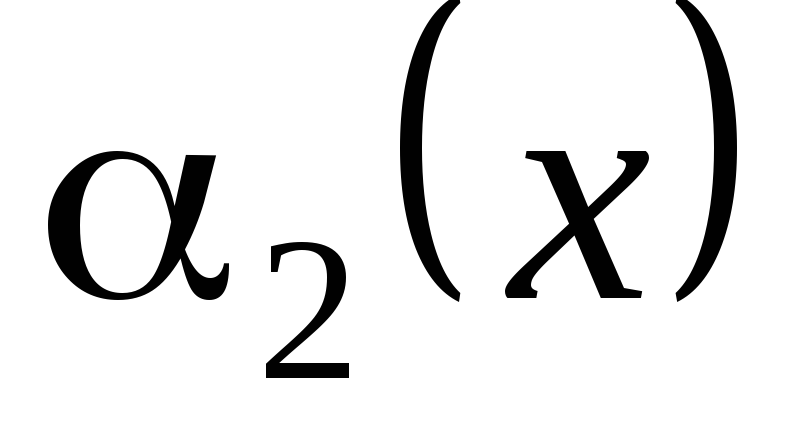 .
.
При
вычислении пределов используют следующие
замены эквивалентных бесконечно малых
функций при
![]() или
или![]() :
:
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,![]() .
.
Следует заметить, что предел отношения бесконечно малых функций равен пределу отношения эквивалентных им бесконечно малых функций.
Замечание:замену бесконечно малых функций на эквивалентные им бесконечно малые функции нельзя производить в случае разности бесконечно малых функций.
1.4. Примеры вычисление пределов
Применяя
теоремы о пределах, а также свойства
бесконечно малых и бесконечно больших
функций, практическое вычисление предела
функции при
![]() сводится к подстановке вместо
сводится к подстановке вместо
![]() его предельного
значения
его предельного
значения
![]() и вычислению значения выражения. При
этом символ
и вычислению значения выражения. При
этом символ ![]() не
пишется.
не
пишется.
Пример 1.
Вычислить
пределы: а)![]() ;
б)
;
б)![]() .
.
Решение.
а)
 .
.
На практике теоремы о пределах, свойства бесконечно малых и бесконечно больших функций учитываются мысленно, решение оформляется следующим образом:
![]() .
.
б)
![]() .
.
Если
в результате подстановки вместо
![]() его предельного
значения
его предельного
значения
![]() невозможно судить о результате, говорят,
что имеет место неопределенность и для
вычисления предела необходимо
преобразование функции – говорят, что
нужно “избавиться от неопределенности”
или “раскрыть неопределенность”.
невозможно судить о результате, говорят,
что имеет место неопределенность и для
вычисления предела необходимо
преобразование функции – говорят, что
нужно “избавиться от неопределенности”
или “раскрыть неопределенность”.
К основным неопределенностям относят следующие случаи, получаемые в результате подстановки:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
В зависимости от вида неопределенности и вида функции, предел которой находят, применяют различные подходы для ее раскрытия.
Например,
если неопределенность
![]() получена при вычислении предела
дробно-рациональной функции (отношения
двух многочленов) при
получена при вычислении предела
дробно-рациональной функции (отношения
двух многочленов) при
![]() ,
то для
раскрытия неопределенности необходимо
разложить на множители числитель и
знаменатель дроби и сократить дробь на
общий множитель
,
то для
раскрытия неопределенности необходимо
разложить на множители числитель и
знаменатель дроби и сократить дробь на
общий множитель
![]() .
На этапе сокращения происходит раскрытие
неопределенности.
.
На этапе сокращения происходит раскрытие
неопределенности.
Пример 2.
Вычислить
предел
![]() .
.
Решение.
Так
как при непосредственной подстановке
вместо
![]() предельного значения
предельного значения![]() получается неопределенность
получается неопределенность![]() и функция дробно-рациональная, разложим
на множители числитель и знаменатель.
и функция дробно-рациональная, разложим
на множители числитель и знаменатель.
![]()
![]()
D= (–1)2– 4·1·(–6) = 1 + 24 = 25D= 12– 4·2·(–21) = 1 + 168 = 169
![]() ;
;![]() .
.![]() ;
;![]() .
.
Тогда
![]() . Тогда
. Тогда![]() .
.
Подставим вместо многочленов их разложения на множители и получим:
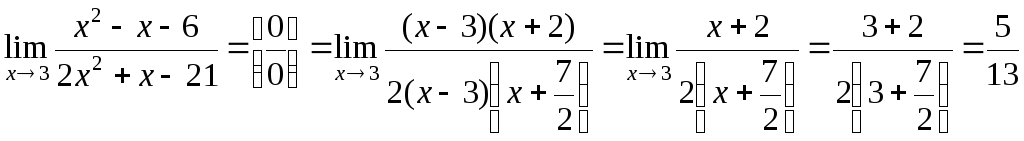 .
.
Если
неопределенность
![]() получена при вычислении предела
дробно-иррациональной функции при
получена при вычислении предела
дробно-иррациональной функции при
![]() ,
то чтобы выделить общий множитель
числителя и знаменателя
,
то чтобы выделить общий множитель
числителя и знаменателя
![]() ,
а затем сократить дробь, необходимо
умножить числитель и знаменатель на
сопряженное выражение для случая
квадратного корня и на неполный квадрат
суммы или разности для случая кубического
корня.
,
а затем сократить дробь, необходимо
умножить числитель и знаменатель на
сопряженное выражение для случая
квадратного корня и на неполный квадрат
суммы или разности для случая кубического
корня.
Пример 3.
Вычислить
пределы: а)
![]() ;
б)
;
б)![]() .
.
Решение.
а)
Так как при непосредственной подстановке
![]() в функцию получается неопределенность
вида
в функцию получается неопределенность
вида ![]() ,
функция
дробно-иррациональная и содержит корень
квадратный, то для раскрытия неопределенности
домножим числитель и знаменатель на
выражение, сопряженное числителю, и
воспользуемся формулой
,
функция
дробно-иррациональная и содержит корень
квадратный, то для раскрытия неопределенности
домножим числитель и знаменатель на
выражение, сопряженное числителю, и
воспользуемся формулой
![]() .
.
![]()
=![]()
=![]()
=![]() .
.
б)
Так как при непосредственной подстановке
![]() в функцию получается неопределенность
вида
в функцию получается неопределенность
вида ![]() ,
функция
дробно-иррациональная и содержит корень
кубический, то для раскрытия неопределенности
домножим числитель и знаменатель на
неполный квадрат суммы для выражения
в знаменателе и воспользуемся формулой
,
функция
дробно-иррациональная и содержит корень
кубический, то для раскрытия неопределенности
домножим числитель и знаменатель на
неполный квадрат суммы для выражения
в знаменателе и воспользуемся формулой
![]() .
.

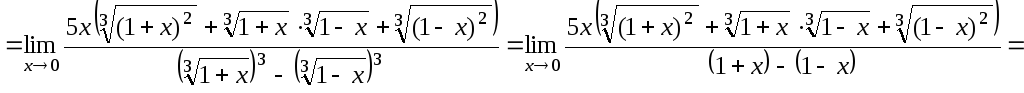
![]()
![]() .
.
Для
раскрытия неопределенности
![]() получаемой при вычислении предела
дробно-рациональной функции при
получаемой при вычислении предела
дробно-рациональной функции при![]() ,
применяют прием вынесения аргумента
,
применяют прием вынесения аргумента![]() самой старшей степени (числителя или
знаменателя) за скобки в числителе и
знаменателе и его последующее сокращение.
самой старшей степени (числителя или
знаменателя) за скобки в числителе и
знаменателе и его последующее сокращение.
Пример 4.
Вычислить
пределы: а) ![]() ;
б)
;
б)
![]() .
.
Решение.
а)
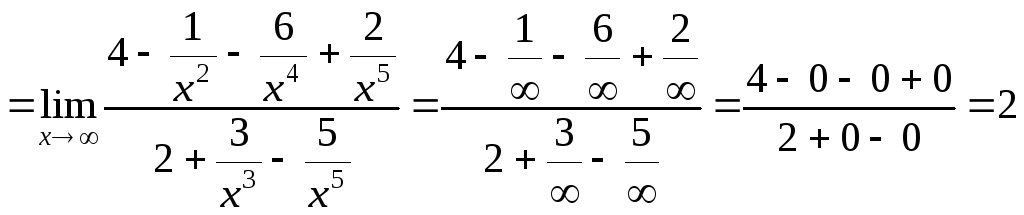 .
.
б)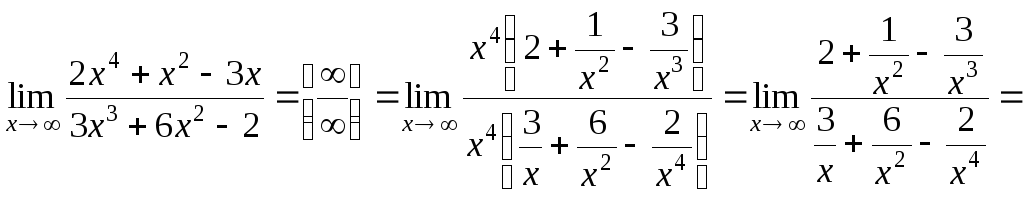
=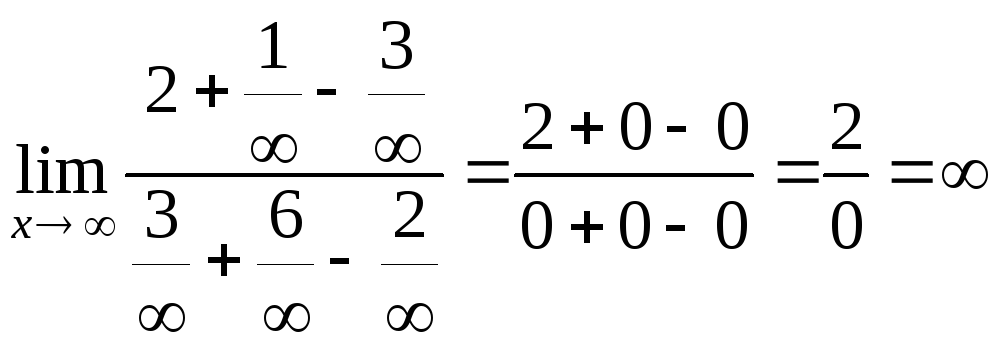 .
.
Если
под знаком предела содержатся
тригонометрические функции, то
неопределенность
![]() раскрывается при помощи преобразований,
приводящих к сокращению дроби и сведению
получившегося выражения к первому
замечательному пределу или его следствиям.
раскрывается при помощи преобразований,
приводящих к сокращению дроби и сведению
получившегося выражения к первому
замечательному пределу или его следствиям.
Пример 5.
Вычислить
предел ![]() .
.
Решение.
Первый способ.
Домножим
числитель и знаменатель дроби на
![]() и
и![]() и воспользуемся первым замечательным
пределом и его следствиями.
и воспользуемся первым замечательным
пределом и его следствиями.
![]()
=![]() .
.
Второй способ.
Этот же предел можно вычислить, используя эквивалентности бесконечно малых тригонометрических функций.
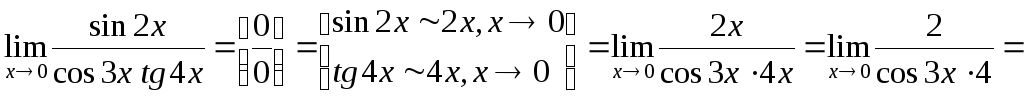
![]()
Неопределенность
вида
![]() раскрывается сведением ко второму
замечательному пределу.
раскрывается сведением ко второму
замечательному пределу.
Пример 6.
Вычислить
предел ![]() .
.
Решение.
Так
как при непосредственной подстановке
![]() получается неопределенность вида
получается неопределенность вида
![]() ,
воспользуемся следствием из второго
замечательного предела, предварительно
преобразовав функцию.
,
воспользуемся следствием из второго
замечательного предела, предварительно
преобразовав функцию.

 .
.
Неопределенность
вида
![]() может сводится к неопределенности вида
может сводится к неопределенности вида
![]() с помощью преобразований. Далее
применяется прием раскрытия неопределенности
вида
с помощью преобразований. Далее
применяется прием раскрытия неопределенности
вида![]() .
.
Пример 7.
Вычислить
предел ![]() .
.
Решение.
Подставим
вместо
![]() предельное
значение:
предельное
значение:
 .
.
Для раскрытия данной неопределенности преобразуем выражение в скобках – выделим целую часть.
![]()
![]()
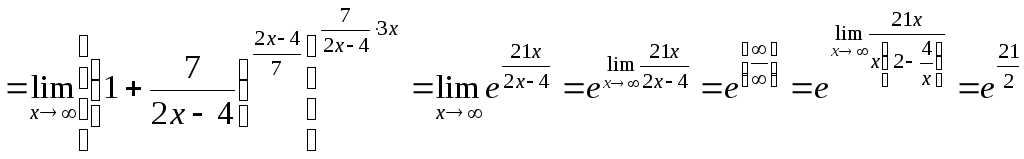 .
.
Неопределенности
![]() ,
,![]() и
и![]() сводят к виду
сводят к виду![]() или
или![]() с помощью преобразования функции к
дроби.
с помощью преобразования функции к
дроби.
Пример 8.
Вычислить
пределы: а) ![]() ;
б)
;
б)
![]() .
.
Решение.
а)
![]() .
.
б)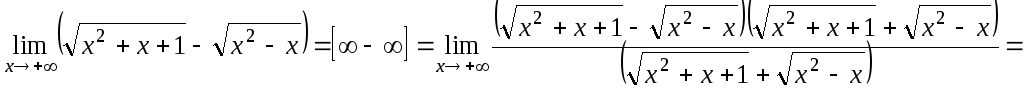


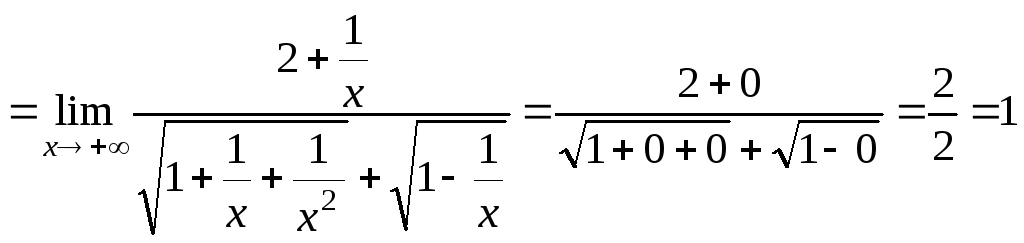 .
.
