Краткие теоретические сведения

1. Пределы и непрерывность функции

1.1. Предел числовой последовательности и функции в точке и на бесконечности. Односторонние пределы функции в точке.

Пусть задано множество всех натуральных чисел, расположенных в порядке их возрастания: .

Если каждому числу из множества натуральных чисел по определённому закону ставится в соответствие одно действительное число , то множество вещественных чисел называетсячисловой последовательностью.

Кратко числовая последовательность обозначается . Чаще всего последовательность задается формулой его общего члена.

Например, общий член определяет последовательность:

.

Число называется пределом числовой последовательности , если для любого сколь угодно малого наперед заданного числаможно найти такой номер последовательности, что для всех членов последовательности с номеромвыполняется неравенство. Графически это означает, что все члены последовательности с номеромнаходятся в промежутке отдо( рис 1).

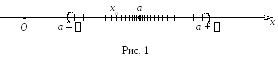
Если такой предел существует, то последовательность называется сходящейся, в противоположном случае – расходящейся.

Предел последовательности обозначается:

Пусть функция определена в некоторой окрестности точки. В самой точке функция может быть и не определена.

Число называется пределом функции в точке (при), если для любой числовой последовательностизначений аргумента(), соответствующая последовательность значений функциистремится к числуа.

Данное определение предела функции графически показано на рис.2. При этом предполагается, что последовательность принадлежит области определения функции.

Таким образом, число называется пределом функции в точке (при), если для любого сколь угодного малого числанайдётся такое число, что для всех значений аргументаудовлетворяющих неравенству, будет выполняться неравенство.

Предел функции в точке обозначается:

.

Иногда бывает так, что предел функции в точке имеет разную величину, когдаслева, т.е.меньше, и когдасправа, т.е.больше. В таком случае говорят ободносторонних пределах функции в точке: левостороннем и правостороннем соответственно.

Левосторонний предел функции в точке обозначается:

.

Правосторонний предел функции в точке обозначается:

.

Число называетсяпределом функции на бесконечности (при ), если для любого сколь угодно малого числа можно указать такое число , что для всех значений аргумента удовлетворяющих неравенству, будет выполняться неравенство.

Предел функции на бесконечности обозначается:

.

Замечание: Обозначение является обобщением дляи. Если выбор знака является принципиальным, то это должно отражаться в условии задания.

1.2. Основные теоремы о пределах

Практическое вычисление пределов основывается на следующих теоремах.

Если существует и , то

1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:

.

2. Предел произведения двух функций равен произведению их пределов:

.

3. Предел частного равен пределу числителя, деленного на предел знаменателя, при условии, что предел знаменателя не равен нулю:

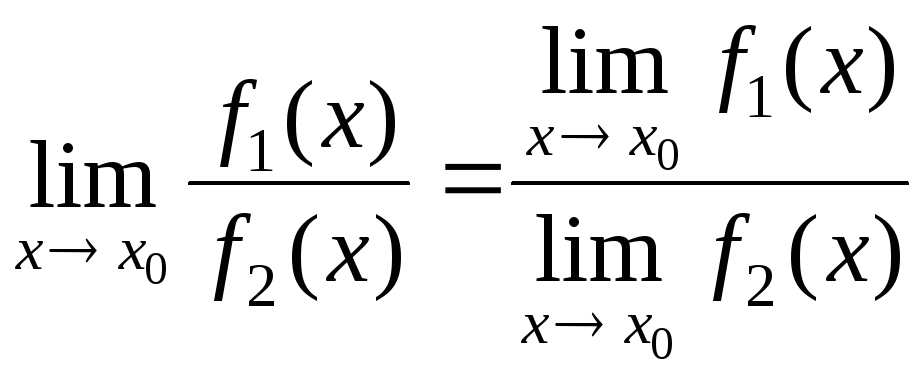, если .

4. Постоянный множитель можно выносить за знак предела:

, если .

5. Предел степени с натуральным показателем равен той же степени предела:

.

Используются также следующие замечательные пределы:

І) (первый замечательный предел).

Следствия из первого замечательного предела:

; ; ; ;

а также:

;;;,

где – некоторая функция.

ІІ) (второй замечательный предел) или .

Следствия из второго замечательного предела:

; ,

где – некоторые функции.