
- •Высшая математика математический анализ функций одной переменной
- •0501 „Экономика и предпринимательство”,
- •0502 „Менеджмент”
- •Издание рассмотрено и рекомендовано к печати на заседании кафедры физико-математических дисциплин (протокол № 5 от 13 января 2009 г.);
- •Содержание
- •Краткие теоретические сведения
- •1. Пределы и непрерывность функции
- •1.1. Предел числовой последовательности и функции в точке и на бесконечности. Односторонние пределы функции в точке.
- •1.2. Основные теоремы о пределах
- •1.3. Бесконечно малые и бесконечно большие функции
- •1.4. Примеры вычисление пределов
- •1.5. Непрерывность функции
- •Вопросы для самоконтроля
- •2. Дифференциальное исчисление функции одной переменной
- •2.1. Производная функции. Геометрический смысл производной функции
- •2.2. Общие правила дифференцирования функции.
- •Основные правила дифференцирования
- •Производная сложной функции
- •Сводная таблица формул дифференцирования
- •Производная обратной функции
- •Дифференцирование функций, заданных параметрически
- •Дифференцирование неявной функции
- •Логарифмическое дифференцирование
- •Производные высших порядков
- •2.3. Дифференциал функции
- •2.4. Применение дифференциального исчисления функции одной переменной
- •2.4.1. Применение производной при вычислении пределов.
- •Правило Лопиталя
- •2.4.2. Возрастание и убывание функции на интервале
- •2.4.3. Экстремумы функции
- •2.4.4. Наибольшее и наименьшее значения функции на отрезке.
- •Значений функции на отрезке:
- •2.4.5. Выпуклость графика функции. Точки перегиба
- •Интервалы выпуклости, вогнутости и точки перегиба:
- •2.4.6. Асимптоты графика функции
- •2.4.7. Полное исследование функции и построения ее графика.
- •2.5. Вопросы для самоконтроля
- •3. Интегральное исчисление функции одной переменной
- •3.1. Неопределенный интеграл
- •3.1.1 Свойства неопределённого интеграла.
- •3.1.2. Таблица неопределенных интегралов
- •3.1.3. Основные методы интегрирования
- •Метод непосредственного интегрирования
- •Метод замены переменной
- •Метод интегрирования по частям
- •3.1.4. Интегрирование дробно-рациональных функций
- •Интегрирование простейших дробей
- •3.1.5. Интегрирование тригонометрических функций.
- •, , .
- •3.1.6. Интегрирование некоторых видов иррациональных функций
- •3.1.7. Интегрирование дифференциального бинома
- •3.1.8. Интегралы, не выражающиеся через элементарные функции
- •3.1.9. Вопросы для самоконтроля
- •3.2. Определенный интеграл
- •3.2.1. Интегральная сумма и определенный интеграл
- •3.2.2. Свойства определенного интеграла
- •3.2.3. Вычисление определенного интеграла
- •Метод замены переменной в определенном интеграле
- •Метод интегрирования по частям в определенном интеграле
- •3.2.4. Несобственные интегралы
- •3.2.5. Геометрические приложения определенного интеграла
- •Вычисление площадей плоских фигур в декартовых координатах
- •Вычисление объема тела вращения
- •Вычисление длины дуги кривой
- •3.2.6. Вопросы для самоконтроля
- •Литература
- •Индивидуальные задания для расчетно-графической работы
- •4) ; 5).
- •Таблицы выбора вариантов заданий для ргр № 2
- •211 Группа
- •212 Группа
- •213 Группа
- •214 Группа
- •215 Группа
- •311 Группа
- •312 Группа
- •313 Группа
- •314 Группа
- •315 Группа
- •316 Группа
- •1111 Группа
- •1112 Группа
- •1211 Группа
- •1212 Группа
- •1311 Группа
- •1312 Группа
- •1313 Группа
- •1511 Группа
- •1512 Группа
3.1.7. Интегрирование дифференциального бинома
Интегралы вида
![]() ,
,
где
![]() – действительные числа,
– действительные числа,![]() – рациональные числа (дроби) называютсяинтегралами
от дифференциального бинома
или интегралами
Чебышева.
– рациональные числа (дроби) называютсяинтегралами
от дифференциального бинома
или интегралами
Чебышева.
Интеграл от дифференциального бинома вычисляют приведением к интегралу от рациональной функции следующими подстановками:
Если
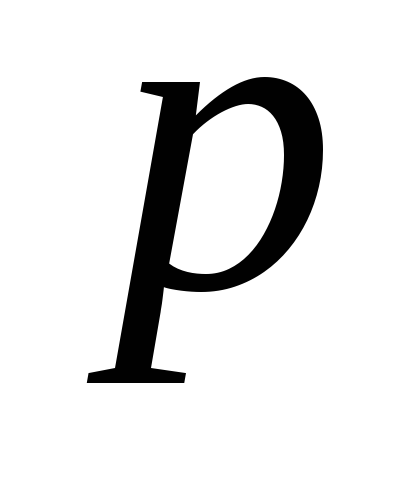 – целое число, то применяют подстановку
– целое число, то применяют подстановку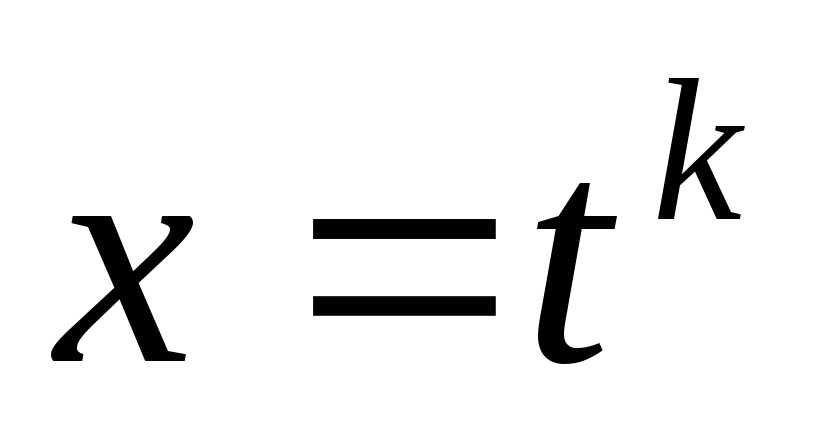 ,
где
,
где – наименьшее общее кратное знаменателей
дробей
– наименьшее общее кратное знаменателей
дробей и
и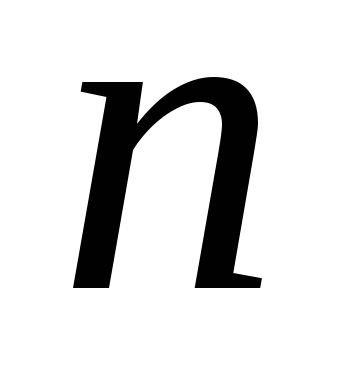 ;
;Если
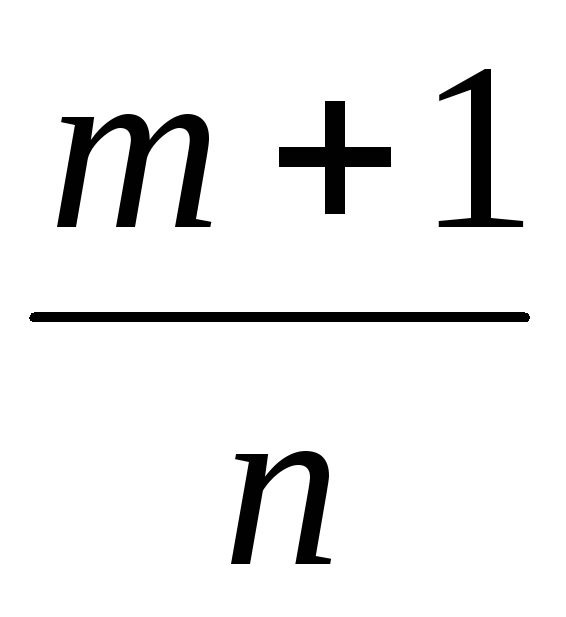 – целое число, то применяют подстановку
– целое число, то применяют подстановку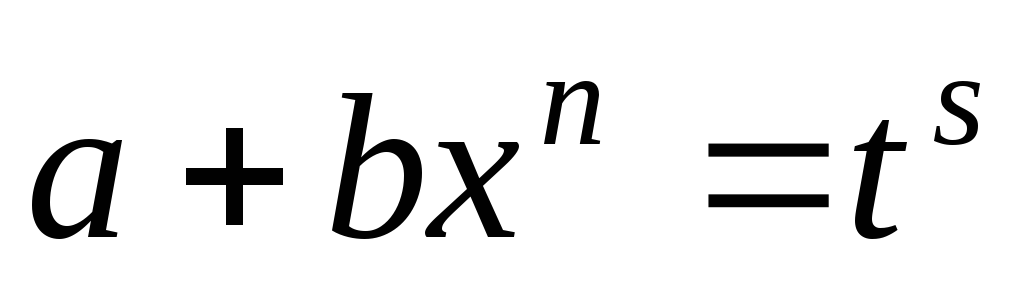 ,
где
,
где – знаменатель дроби
– знаменатель дроби ;
;Если
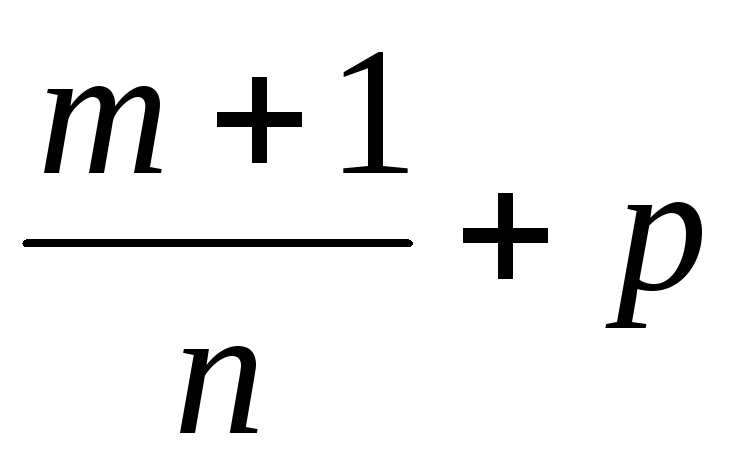 – целое число, то применяют подстановку
– целое число, то применяют подстановку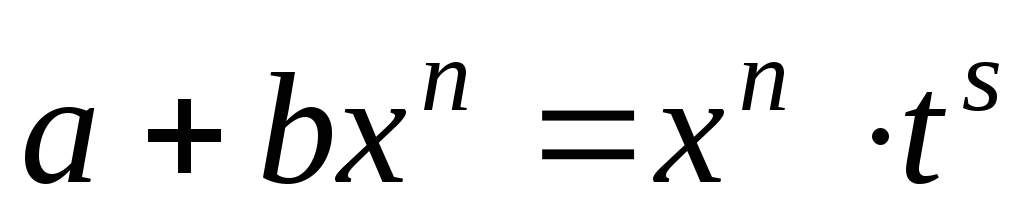 ,
где
,
где – знаменатель дроби
– знаменатель дроби ;
;
Во
всех остальных случаях интегралы вида
![]() не выражаются через элементарные
функции, т.е. «не берутся».
не выражаются через элементарные
функции, т.е. «не берутся».
Пример 37.
Найти
интеграл
![]() .
.
Решение.
Перепишем
интеграл
 .
.
В
данном случае показатели
![]() .
.
Так
как
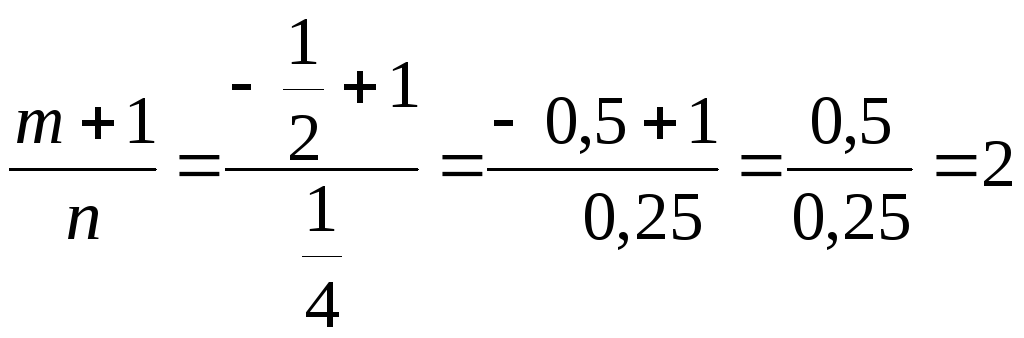 – целое число, то мы имеем дело со вторым
случаем и применим подстановку
– целое число, то мы имеем дело со вторым
случаем и применим подстановку![]() ,
где
,
где![]() – знаменатель дроби
– знаменатель дроби![]() ,
т.е.
,
т.е.![]() .
Получаем:
.
Получаем:
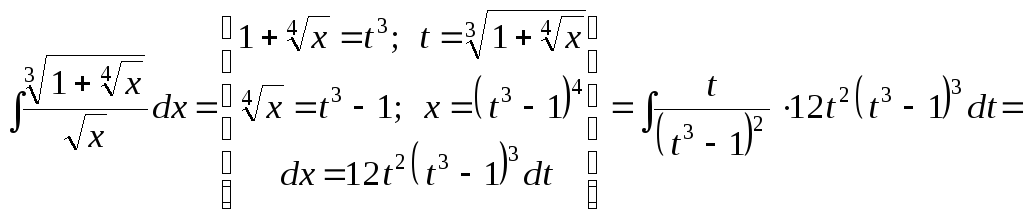
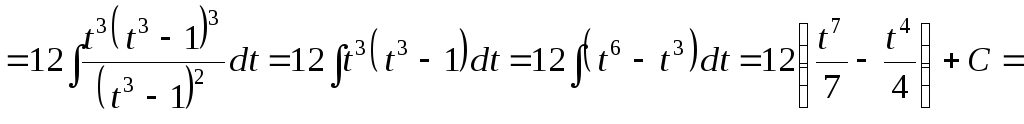
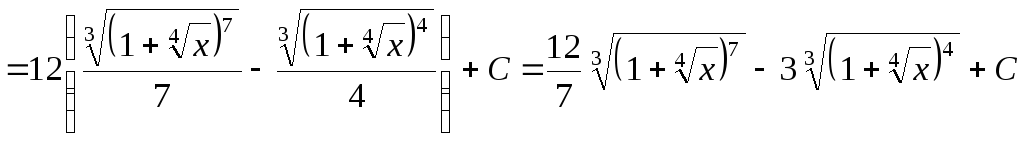 .
.
3.1.8. Интегралы, не выражающиеся через элементарные функции
Изученные методы интегрирования позволяют во многих случаях вычислить неопределенный интеграл от основных классов элементарных функций, т.е. для подынтегральной элементарной функции найти первообразную функцию, которая является также элементарной функцией. Однако имеется ряд интегралов от элементарных функций, которые не выражаются через элементарные функции, т.е. не вычисляются. К таким интегралам относят интегралы вида:
![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() и др.
и др.
Указанные интегралы не могут быть найдены с помощью рассмотренных выше методов интегрирования. Для их решения используют методы, изучаемые в других разделах высшей математики.
3.1.9. Вопросы для самоконтроля
Что называется первообразной функцией?
Что называется неопределенным интегралом?
Как выполняется проверка правильности нахождения неопределенного интеграла?
Перечислите основные свойства неопределенного интеграла.
Перечислите интегралы, входящие в таблицу неопределенных интегралов.
В чем заключается метод непосредственного интегрирования?
В чем заключается интегрирование методом подстановки?
В чем заключается метод интегрирования по частям?
Сформулируйте формулу интегрирования по частям.
Как интегрируются простейшие дроби четырех типов?
Какие приемы используют при интегрировании рациональных дробей?
Какие подстановки используют при интегрировании тригонометрических функций?
Какие подстановки используют при интегрировании иррациональных функций?
Какие подстановки используются при интегрировании дифференциального бинома
Какие интегралы не выражаются через элементарные функции?
3.2. Определенный интеграл
3.2.1. Интегральная сумма и определенный интеграл
Пусть
функция
![]() определена и ограничена на отрезке
определена и ограничена на отрезке
![]() оси
оси
![]() .
.
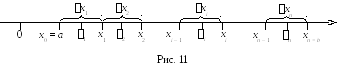
Разобьем
этот отрезок на
![]() частей, не обязательно равных, точками
частей, не обязательно равных, точками![]() .
Получим элементарные отрезки
.
Получим элементарные отрезки![]() ,
где
,
где![]() .
На каждом отрезке
.
На каждом отрезке![]() возьмем произвольную точку
возьмем произвольную точку![]() и вычислим значение функции
и вычислим значение функции![]() в каждой выбранной точке.
в каждой выбранной точке.
Составим сумму
![]() ,
,
которая
называется интегральной
суммой
функции
![]() на отрезке
на отрезке
![]() .
.
Для
данной функции
![]() на отрезке
на отрезке
![]() можно составить бесчисленное множество
интегральных сумм, так как построение
интегральной суммы заключается в
произвольном делении заданного отрезка
на элементарные отрезки и произвольном
выборе точек
можно составить бесчисленное множество
интегральных сумм, так как построение
интегральной суммы заключается в
произвольном делении заданного отрезка
на элементарные отрезки и произвольном
выборе точек
![]() на каждом
элементарном отрезке. Обозначим через
на каждом
элементарном отрезке. Обозначим через
![]() – длину наибольшего из элементарных
отрезков.
– длину наибольшего из элементарных
отрезков.
Предел
интегральной суммы при условии, что
![]() стремится к нулю, если этот предел
существует и не зависит от способа
разбиения отрезка
стремится к нулю, если этот предел
существует и не зависит от способа
разбиения отрезка
![]() на части и от выбора в каждой части точки
на части и от выбора в каждой части точки
![]() ,
называетсяопределенным
интегралом
от функции
,
называетсяопределенным
интегралом
от функции
![]() в пределах от
в пределах от![]() до
до![]() и обозначается
и обозначается![]() .
.
![]() ,
,
где ![]() – нижний
предел интегрирования;
– нижний
предел интегрирования;
![]() – верхний предел интегрирования;
– верхний предел интегрирования;
![]() –переменная
интегрирования;
–переменная
интегрирования;
![]() – подынтегральная функция;
– подынтегральная функция;
![]() –подынтегральное
выражение.
–подынтегральное
выражение.
Функция,
для которой на отрезке
![]() существует определенный интеграл,
называется интегрируемой
на этом отрезке.
Для интегрируемости достаточно, чтобы
на отрезке
существует определенный интеграл,
называется интегрируемой
на этом отрезке.
Для интегрируемости достаточно, чтобы
на отрезке
![]() функция была непрерывна или имела
конечное число разрывов первого рода.
функция была непрерывна или имела
конечное число разрывов первого рода.
Если
для непрерывной на отрезке
![]() подынтегральной функции
подынтегральной функции
![]() может быть найдена первообразная функция
может быть найдена первообразная функция![]() ,
то определенный интеграл от этой функции
вычисляется поформуле
Ньютона-Лейбница
как приращение первообразной на
этом отрезке:
,
то определенный интеграл от этой функции
вычисляется поформуле
Ньютона-Лейбница
как приращение первообразной на
этом отрезке:
![]()
Пример 38.
Вычислить
определенные интегралы: а)![]() ;
б)
;
б)![]() .
.
Решение.
а)
![]() ;
;
б)
![]() .
.
