3.1.2. Таблица неопределенных интегралов

Т.к. интегрирование есть действие обратное дифференцированию, то можно получить таблицу основных интегралов, применяя таблицу производных и свойства неопределенного интеграла.

1. . 11..

2. . 12..

3. . 13..

4. . 14..

5. . 15.,.

6. . 16.,.

7. . 17.,.

8. . 18.,.

9. . 19..

10. . 20..

Если и– произвольная функция, которая имеет непрерывную производную, то

.

Это свойство (его называют инвариантностью формул интегрирования) означает, что та или иная формула для неопределенного интеграла остается справедливой независимо от того, переменная интегрирования – есть независимая переменная или произвольная функция от нее.

3.1.3. Основные методы интегрирования

Не существует универсального метода нахождения неопределенных интегралов. К основным методам интегрирования относят следующие методы: непосредственное интегрирование, метод замены переменной (метод подстановки) и метод интегрирования по частям.

Метод непосредственного интегрирования

Метод непосредственного интегрирования применяется, когда неопределенный интеграл можно найти непосредственно с помощью таблицы интегралов и свойств неопределенных интегралов. В некоторых случаях подынтегральную функцию необходимо преобразовать, чтобы свести заданный интеграл к табличному интегралу.

Замечание: При нахождении алгебраической суммы интегралов обычно пишут одну произвольную постоянную в конце.

Пример 23.

Найти интегралы: а); б);

в); г).

Решение.

а)

.

б)

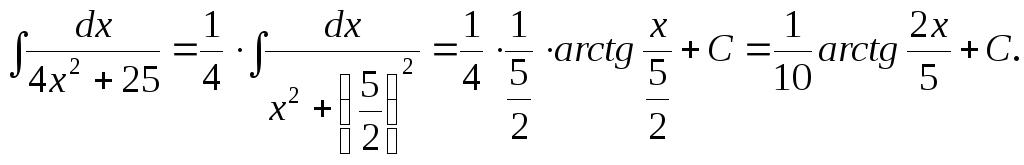
в)

=.

г)

.

Метод замены переменной

Метод замены переменной (метод подстановки) заключается в введении новой переменной интегрирования (т.е. подстановки) . При этом заданный интеграл приводится к новому интегралу, который должен является табличным или к нему сводящимся.

Метод замены переменной описывается следующей формулой:

.

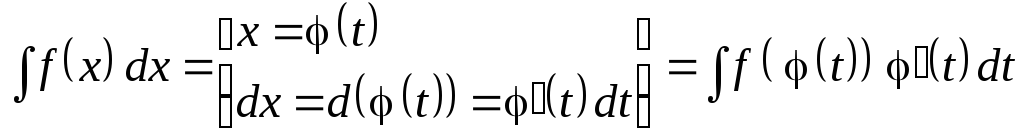Замечание: не существует общего правила выбора подстановок. Умение правильно подобрать подстановку определяется опытом или видом подынтегральной функции.

Часто формулу замены переменной применяют также и в обратном порядке: применяют подстановку , т.е. часть подынтегральной функции обозначается через новую переменную. Затем из замены выражают переменную, находят дифференциали подставляют все в исходное подынтегральное выражение. После нахождения интеграла от новой переменнойвозвращаются к старой переменной. Для этого подхода справедлива формула:

.

Замечание: если подынтегральное выражение содержит некоторую функцию и ее дифференциал с точностью до коэффициента, то выражать переменную из подстановкинеобязательно.

Пример 24.

Найти интегралы: а) ; б); в).

Решение.

а)

.

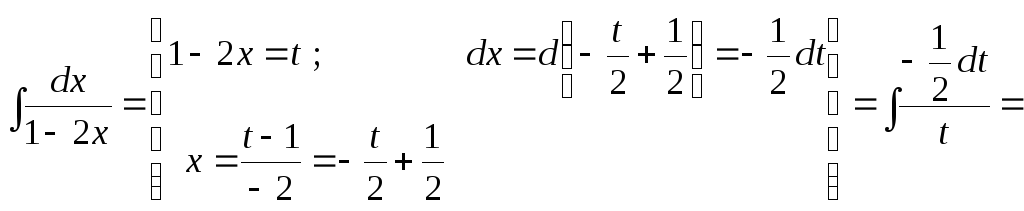
б)

.

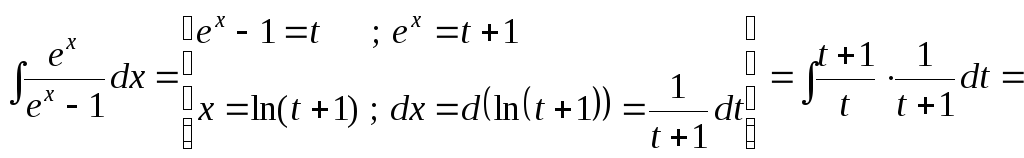
в) .

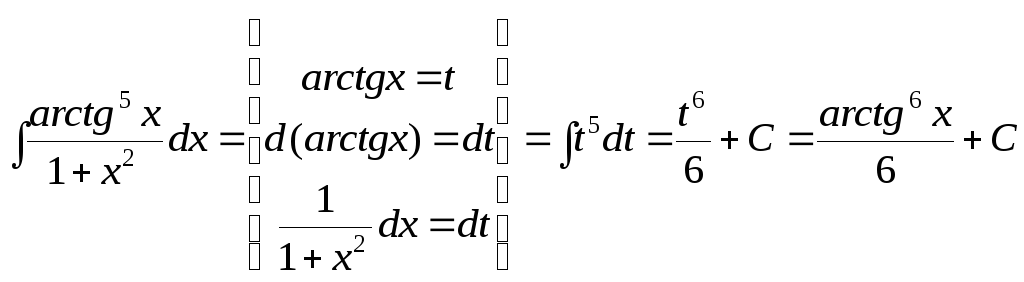Замечание: рассмотрим случай, когда существует возможность замены линейного выражения , приводящей к табличному интегралу (см. Пример 24а); так называемую линейную подстановку.

Если известна первообразная для некоторой функции:

,

то ,

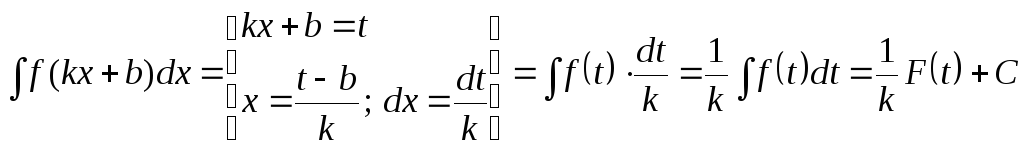т.е. .

Используя данную замечание, можно расширить возможность применения табличных интегралов, например:

;

;

;

.

Пример 25.

Найти интегралы, используя замечание о линейной подстановке:

а) ; б); в); г).

Решение.

а) ;

б) ;

в) ;

г)