
14_08_18_ТАУ_1,2_Лекционный курс
.pdfПри S = 0 передаточная функция равняется:
Wв(0) |
= |
Коб |
|
. |
|
(7.9) |
||
|
|
|
|
|
||||
|
1+ К рКоб |
|
|
|||||
Статическая ошибка по возмущению (рис. 7.4): |
|
|||||||
ств |
= F (0) |
|
|
Коб |
. |
(7.10) |
||
|
+ К рКоб |
|||||||
1 |
|
|||||||
|
|
|
||||||
Из формулы (7.10) видно, что чем больше коэффициент усиления регулятора, тем меньше влияет возмущение на отклонение управляемого параметра Y(S) .
Таким образом, при наличии пропорционального регулятора, замкнутая система регулирования (регулятор и объект регулирования не содержат интегратора) имеет статическую ошибку по управлению и по возмущению.
Рассмотрим в качестве регулятора интегрирующее звено:
W1( s) = |
|
К р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.11) |
||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При интегральном регуляторе передаточная функция замкнутого контура |
||||||||||||||||||||
по управлению примет вид: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
К р |
|
|
Коб |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
К рKоб |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
y(s) |
|
|
|
s 1 + Т s |
|
|
|||||||||||
Wу ( s) = |
|
|
|
|
|
|
|
|
|
|
|
|
об |
|
. |
(7.12) |
||||
|
|
|
= |
|
|
|
|
|
|
|
= |
|
||||||||
|
x(s) |
|
|
|
К р |
|
s(1 + Тоб s) + К рKоб |
|||||||||||||
|
|
|
|
1 + |
× |
Коб |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
s |
|
1 + Тоб s |
|
|
|
||||||
При S = 0 Wу (s) =1.
Ошибка по управлению в соответствии с уравнением (7.1) равна нулю (рис. 7.6):
ст |
у |
= x(0)Wу (0) − x(0) = x(0) ×1− x(0) = 0 . |
(7.13) |
|
|
|
Эквивалентная передаточная функция по возмущению при интегральном регуляторе имеет вид:
|
|
|
|
Коб |
|
|
|
|
||||
Wв ( s) = |
|
|
1 + Тоб s |
Кобs |
|
|||||||
|
|
|
|
|
= |
|
. |
(7.14) |
||||
|
|
|
|
|
|
|||||||
|
1 + |
К р |
× |
Коб |
s(1 + Тоб s) + К рКоб |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
s |
1 + Тоб s |
|
|
|
|||||
71
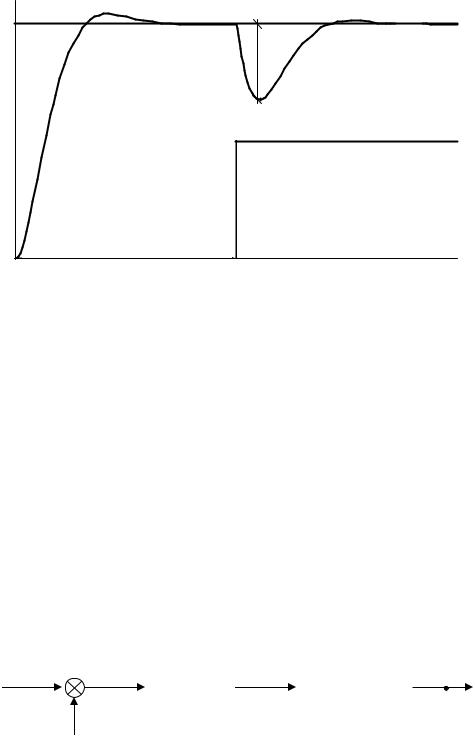
|
X |
сту = 0 |
дин |
ств = 0 |
|
||
|
|
Y |
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
T |
|
|
Рисунок 7.6 - График переходных процессов в системе при наличии |
|||||||
интегратора в регуляторе. |
|
|
|
|
|
||
При |
S = 0 |
Wв ( s) = 0. |
Таким |
образом, |
статическая |
ошибка |
по |
возмущению, при наличии интегратора в составе регулятора, равна нулю |
|||||||
(рис. 7.6): |
|
|
|
|
|
|
|
ст = F(0) ×0 = 0 . |
(7.15) |
в
Таким образом, применение регулятора в виде интегрирующего звена приводит к устранению статической ошибки по управлению и возмущению.
7.2. Выбор типа регулятора
Классическая схема управления с единичной отрицательной обратной связью показана на рис. 7.7.
X |
|
U P |
Объект |
Y |
|||
|
|
|
|
Регулятор |
|
||
|
|
|
|
|
управления |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 7.7 - Управление с отрицательной обратной связью Назначение регулятора системы заключается в коррекции динамических
свойств объекта управления с помощью управляющего сигнала U P так, чтобы
выходной |
сигнал Y |
как можно меньше отличался от желаемого входного |
сигнала X |
(сведение |
к минимуму (нулю) рассогласования ). Регулятор |
72
вырабатывает управляющий сигнал, используя ошибку регулирования
= X − Y .
Для оценки динамических свойств системы часто рассматривается реакция на единичное ступенчатое воздействие. Переходной процесс должен отвечать заданным показателям качества, к которым относятся время переходного процесса, перерегулирование и колебательность.
Основные типы линейных непрерывных регуляторов и законы регулирования.
П - регулятор - регулирование по отклонению действительного значения управляемого параметра от заданного значения. Передаточная функция регулятора:
Wп ( s) = K p . |
|
(7.16) |
|||
И - регулятор – регулирование по интегралу отклонения по времени. |
|||||
Передаточная функция регулятора: |
|
||||
1 |
|
|
|
||
Wи (s) = |
|
|
. |
(7.17) |
|
Тиs |
|||||
|
|
|
|||
где Ти – постоянная времени интегрирования регулятора.
При увеличении Ти переходный процесс затягивается, при уменьшении
– ускоряется, но при этом снижается запас устойчивости. Переходный процесс приобретает выраженный колебательный характер, и при дальнейшем
уменьшении Ти система регулирования теряет устойчивость.
ПД - регулятор – регулирование по отклонению и производным
отклонения по времени. Передаточная функция регулятора: |
|
Wпд (s) = K р (1+ Тдs) . |
(7.18) |
где Тд – постоянная времени дифференцирующего звена.
Дифференциальная составляющая в формуле (7.18) позволяет повысить быстродействие регулятора.
На практике реализовать идеальное дифференцирование невозможно, так как частотная характеристика звена бесконечно увеличивается на высоких частотах. Поэтому используют дифференцирующее звено с дополнительным фильтром:
|
|
Тдs |
|
|
||
Wпд ( s) = K р 1+ |
|
|
|
|
. |
(7.19) |
Т |
|
s +1 |
||||
|
ф |
|
|
|||
|
|
|
|
|
|
|
73

где Тф – постоянная времени фильтра (обычно в 3-10 раз меньше, чем Тд).
Чрезмерное увеличение Тд может привести к неустойчивости системы, уменьшение этой величины затягивает переходный процесс.
ПИ - регулятор - регулирование по отклонению и интегралу отклонения по времени. Передаточная функция регулятора:
|
|
1 |
|
|
Wпи ( s) = K р 1 |
+ |
|
. |
(7.20) |
|
||||
|
|
Тиs |
|
|
Наличие пропорциональной составляющей в выражении (7.20) увеличивает быстродействие по сравнению с И - регулятором. Интегральная составляющая в формуле (7.20) позволяет ликвидировать статическую ошибку управления. Из-за наличия интегральной составляющей, система становится астатической как по задающему, так и по возмущающему воздействиям.
ПИД - регулятор - регулирование по отклонению, интегралу и производной отклонения по времени. Передаточная функция регулятора:
|
|
Тдs |
|
|
1 |
|
|
|
||
Wпид (s) = K р 1+ |
|
|
|
|
+ |
|
|
|
. |
(7.21) |
Т |
|
s +1 |
Т |
|
|
|||||
|
ф |
|
и |
s |
|
|||||
|
|
|
|
|
|
|
|
|
||
С помощью правильно настроенного ПИД - регулятора в большинстве случаев удается обеспечить выполнение всех требований к системе. ПИД - регуляторы получили широкое распространение при управлении производственными и технологическими процессами. По статистике более 90%
всех |
промышленных |
регуляторов |
представляют |
собой |
именно |
||
ПИД - регуляторы. |
|
|
|
|
|
|
|
|
Существует инженерный подход к синтезу ПИД - регуляторов (методика |
||||||
Зиглера-Николса), который предусматривает следующие шаги. |
|
||||||
|
1. Коэффициенты |
kd и ki |
устанавливаются |
равными |
нулю, а |
||
коэффициент k p увеличивается до |
тех |
пор, |
пока система не |
потеряет |
|||
устойчивость. |
|
|
|
|
|
|
|
|
2. Предельное значение k p обозначается как kи , а период автоколебаний |
||||||
как |
ри . |
|
|
|
|
|
|
|
3. Значения коэффициентов ПИД - регулятора рассчитываются по |
||||||
следующим формулам: k p = 0.6kи ; ki =1.2kи |
ри ; kd = 3kи ри 40 . |
||||||
74

В промышленных ПИД - регуляторах коэффициенты настраиваются вручную.
Эти расчеты приближенные. Для более точных расчетов предназначен пакет Matlab. В составе Matlab Simulink есть пакет Nonlinear Control Design (NCD) Blockset, с помощью которого можно выполнить оптимизацию параметров ПИД - регулятора, если есть модель объекта управления.
8.Устойчивость линейных систем автоматического управления
8.1.Понятие устойчивости
Система называется устойчивой, если:
после снятия воздействия по окончании переходного процесса система возвращается в исходное равновесное состояние;
после изменения воздействия на постоянную величину по окончании переходного процесса система приходит в новое равновесное состояние.
Понятие устойчивости неразрывно связано с понятием равновесия. Равновесным состоянием тела (или некой системы) называется такое
состояние, в котором сумма всех внешних по отношению к телу (или системе) воздействий равна нулю. Равновесное состояние может быть устойчивым, неустойчивым и нейтральным.
Классической иллюстрацией этого положения (рис. 8.1) является поведение шарика, помещенного: на дно лунки (рис. 8.1, а), на вершину холма (рис. 8.1, б) и на горизонтальную плоскость (рис. 8.1, в).
а |
б |
в |
г |
Рисунок 8.1 - Механическая интерпретация понятия устойчивости В каждом из этих случаев сумма внешних сил, действующих на шарик,
равна нулю и, следовательно, шарик находится в состоянии равновесия. Однако, если в первом случае после небольшого отклонения шарик через некоторое время вновь возвращается в исходное положение равновесия, то во
75

втором он будет продолжать отклоняться от него, а в третьем - просто перейдет в новое положение равновесия, зависящее от величины отклонения. Некоторые системы могут быть неустойчивы при больших воздействиях (рис. 8.1, г).
На рис. 8.2. показаны типовые кривые переходных процессов в неустойчивой (рис. 8.2, а) и устойчивой (рис. 8.2, б) системах. Если система неустойчивая, то любого толчка достаточно, чтобы в ней начался расходящийся процесс выхода из начального установившегося состояния. Этот процесс может быть апериодическим (рис. 8.2, а, кривая 1) или колебательным (рис. 8.2, а, кривая 2).
Рисунок 8.2 - К понятию устойчивости системы Апериодический расходящийся процесс может, например, возникнуть в
САУ, если в ее управляющем устройстве по ошибке переключить полярность обратной связи, в результате чего управляющее устройство будет осуществлять не отрицательную, а положительную обратную связь по выходной величине. При этом управляющее воздействие будет не устранять отклонение, а действовать в обратном направлении, вызывая лавинообразное его изменение.
В случае устойчивой системы (рис. 8.2, б) переходной процесс, вызванный каким-то воздействием, со временем затухает, и система вновь возвращается в устойчивое состояние.
Таким образом, устойчивую систему можно определить также как систему, переходные процессы в которой являются затухающими.
Приведенное понятие устойчивости определяет устойчивость установившегося режима системы. Однако, система может работать в условиях непрерывно изменяющихся воздействий, когда установившийся режим работы отсутствует. С учетом таких условий работы можно дать следующее, более общее определение устойчивости: система устойчива, если ее исходное состояние остается ограниченным в условиях действия на систему ограниченных по величине возмущений.
76
Нетрудно показать, что если переходной процесс в системе затухающий, то система будет удовлетворять и последнему определению.
Как было показано ранее, если все корни характеристического уравнения находятся в левой комплексной полуплоскости, то система регулирования устойчива. К сожалению, вычисление корней просто лишь для уравнений первой и второй степени. Поэтому большое значение приобретают правила, позволяющие определять устойчивость системы без вычисления корней. Эти правила называют критериями устойчивости.
К основным критериям устойчивости относятся алгебраический критерий Гурвица и частотные критерии Михайлова и Найквиста. Рассмотрим частотный критерий устойчивости Найквиста.
8.2. Критерий Найквиста
Критерий предназначен для анализа устойчивости замкнутых систем. Этот критерий позволяет судить об устойчивости замкнутой САУ по виду амплитудно-фазовой характеристики разомкнутой САУ.
Исследование разомкнутой САУ проще, чем замкнутой. Устойчивость разомкнутой системы часто можно установить без всяких вычислений непосредственно по схеме системы. Так, например, разомкнутая система, которая состоит из устойчивых звеньев и не содержит обратных связей, априори устойчива.
Запишем передаточную функцию разомкнутой системы в виде:
WP ( S) = |
B( S) |
|
|
|
, |
(8.1) |
|
|
|||
|
A( S) |
|
|
и преобразуем это выражение в комплексный коэффициент усиления разомкнутой системы:
WP (Iω) = |
|
B(Iω) |
|
|||
|
|
. |
|
(8.2) |
||
|
||||||
|
|
|
A(Iω) |
|
||
Передаточная функция замкнутой системы регулирования, охваченной |
||||||
единичной обратной связью: |
|
|||||
Wз (s) = |
|
Wp (s) |
|
|||
|
|
. |
(8.3) |
|||
|
|
|||||
1 |
+Wp ( s) |
|
||||
Комплексный коэффициент усиления замкнутой системы:
77
|
|
|
|
|
B(iω) |
|
|
||
|
Wp (iω) |
|
|
|
|
|
|
|
|
Wз (iω) = |
= |
|
|
A(iω) |
|
= |
|||
1+Wp (iω) |
1+ |
B(iω) |
|
||||||
|
|
|
|
||||||
|
|
|
A(iω) |
|
|
||||
B(iω)
|
. |
(8.4) |
A(iω) + B(iω) |
Рассмотрим функцию, которая представляет собой знаменатель комплексного коэффициента усиления замкнутой системы регулирования:
|
A(Iω) + B(Iω) |
|
D(Iω) |
|
Iψ (ω) |
|
|
K (Iω) =1+WP (Iω) = |
= |
= |
D(ω)E |
. (8.5) |
|||
A(Iω) |
A(Iω) |
A(ω)EIϕ(ω) |
|||||
|
|
|
|
Знаменатель функции (8.5) представляет собой характеристическое уравнение разомкнутой системы, а числитель характеристическое уравнение замкнутой системы.
Если разомкнутая система устойчива, то изменение фазы Ap (iω) при
росте ω от нуля до ∞ будет равно:
lim |
ϕ (ω ) = N |
π |
, |
|
|
|
(8.6) |
||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
ω→∞ |
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
где N - степень характеристического уравнения разомкнутой системы. |
|
||||||||
Для того чтобы система была устойчива в замкнутом состоянии, |
|||||||||
изменение фазы ψ (ω) |
|
при изменении |
ω |
от нуля до бесконечности также |
|||||
|
|
|
π |
|
|
|
|
|
|
должно стремиться к N |
|
. |
|
|
|
|
|||
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
||
Отсюда вытекает, что изменение фазы K (Iω) должно равняться: |
|
||||||||
lim |
arg K (Iω ) = lim ψ (ω ) |
− lim |
ϕ (ω) = 0 . |
(8.7) |
|||||
ω→∞ |
|
|
|
|
ω→∞ |
ω→∞ |
|
||
|
|
|
|
|
|
||||
Это означает, что годограф K (Iω) |
не |
должен охватывать начало |
|||||||
координат.
Из уравнения (8.5) запишем функцию для амплитудно-фазовой частотной характеристики разомкнутой системы:
Wр (iω) = K (iω) −1. |
(8.8) |
На основании уравнения (8.8) формулируется частотный критерий |
|
Найквиста [2]. Если разомкнутая |
система устойчива, то для устойчивости |
78

замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы не охватывала точку ( −1, I0) .
Рисунок 8.3 - Пример устойчивой системы
Рисунок 8.4 - Пример неустойчивой системы
8.3.Понятие запаса устойчивости
Вусловиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания
ит.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать САУ так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости.
79

Согласно критерию Найквиста, чем дальше АФХ от критической точки
( −1, I0) , тем больше запас устойчивости. Различают запасы устойчивости по модулю и по фазе.
Запас устойчивости по модулю характеризует удаление годографа АФХ разомкнутой САУ от критической точки в направлении вещественной оси и определяется расстоянием H от критической точки до точки пересечения годографом оси абсцисс (рис.8.5, а).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IM |
|
Im |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
RE |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
б) |
|
Рисунок 8.5 - Запас устойчивости Запас устойчивости по фазе характеризует удаление годографа от
критической точки по дуге окружности единичного радиуса и определяется углом ϕ между отрицательным направлением вещественной полуоси и лучом, проведенным из начала координат в точку пересечения годографа с единичной окружностью.
С ростом коэффициента передачи разомкнутой САУ растет модуль каждой точки АФХ и при некотором значении К = Ккр АФХ пройдет через критическую точку (рис. 8.5, б) и попадет на границу устойчивости, а при
К > Ккр замкнутая САУ станет неустойчива.
Обычно при создании САУ задаются требуемыми запасами устойчивости
H и ϕ , за пределы которых она выходить не должна.
8.4. Анализ устойчивости по ЛЧХ
Оценку устойчивости по критерию Найквиста удобнее производить по логарифмическим частотным характеристикам разомкнутой САУ. Очевидно, что каждой точке АФХ будут соответствовать определенные точки ЛАЧХ и ЛФЧХ.
Пусть известны частотные характеристики двух разомкнутых САУ (рис. 8.6, 1 и 2), отличающихся друг от друга только коэффициентом передачи
80
