Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальная металлургическая академия Украины

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

14_08_18_ТАУ_1,2_Лекционный курс

.pdf

Скачиваний:

Добавлен:

12.02.2016

Размер:

5.42 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 156 7 8 9 10 11 12 13 14 15 > Следующая >>>

R2	.	(6.25)
K =

Предполагается, что передача сигнала от входа звена к выходу звена осуществляется мгновенно (безинерционно). Поэтому пропорциональные звенья называют безинерционными.

Если на вход пропорционального звена подать синусоидальный сигнал:

X (T ) = ASIN ωT ,	(6.26)
то на выходе появится сигнал, усиленный в K раз:
y (t ) = KASIN ωt .	(6.27)
Графики ЛАЧХ и ЛФЧХ для такого звена при изменении ω	от 0 до
10 C−1 и K = 2 приведены на рис. 6.8.

Рисунок 6.8 - ЛАЧХ и ЛФЧХ пропорционального звена
Частотные функции звена:
W (Iω) = K .	(6.28)
U (ω) = K .	(6.29)
V (ω ) = 0 .	(6.30)

A(ω) = U(ω)

(6.31)

+V (ω) = K .

(ω)

ϕ(ω) = arctg

= arctg (0) = 0 .

(6.32)

U (ω)

L(ω) = 20lg A(ω) = 20lg K .

(6.33)

Как и следовало ожидать, запаздывание по фазе выходного сигнала

отсутствует.

6.3. Интегрирующее звено

Уравнение интегрирующего звена:

y (t ) = K ∫ x(t ) dt .

(6.34)

Передаточная функция звена

W (S) =

(6.35)

Примером такого звена является усилитель постоянного тока с

конденсатором в цепи обратной связи (рис. 6.9).

Д1

Рисунок 6.9 - Интегратор на базе операционного усилителя Коэффициент передачи для такой электрической схемы определяется

выражением:

K =	1
		.	(6.36)

	R1C1

Если, на вход интегратора подать единичный ступенчатый сигнал, то выходной сигнал будет изменяться в соответствии с выражением:

y(t ) = Kt .	(6.37)
График переходной характеристики изображен на рис. 6.10.

H(T )

10 (T )

Рисунок 6.10 - График переходной характеристики интегрирующего звена

Графики ЛАЧХ и ЛФЧХ при изменении ω от 0 до 10 C−1 и значении K = 3, изображены на рис. 6.11.

Рисунок 6.11 - ЛАЧХ и ЛФЧХ интегрирующего звена
Частотные функции звена:
W (Iω) =	K	=	IK	= −I	K	.	(6.38)

	Iω IIω				ω
U (ω) = 0.							(6.39)

V (ω ) = −

(6.40)

A(ω) = U(ω)

+V (ω)

(6.41)

(ω)

ϕ(ω) = arctg

= −arctg (∞) = −

(6.42)

U (ω)

L(ω) = 20lg A(ω) = 20lg

= 20lg K − 20lgω

(6.43)

L(ω) представляет собой прямую, имеющую наклон минус 20 дБ/дек. Действительно, при увеличении ω на декаду, т.е. в десять раз,

L10(ω) = 20lg ( K ) − 20lg (10ω) = 20lg ( K ) − 20lg (ω) − 20lg (10). Таким образом, величина L10(ω) уменьшилась на 20lg(10) , т.е. на

20 дБ.

Запаздывание по фазе выходного сигнала ϕ(ω) = − .

6.4. Дифференцирующее звено

Уравнение дифференцирующего звена:

y(t ) = K	dx(t )	.	(6.44)

	dt

Передаточная функция звена
W (S) = KS .			(6.45)

Примером такого звена является усилитель постоянного тока с конденсатором в цепи задания (рис. 6.12).

X	C1	Y
		Y
		Д1

Рисунок 6.12 - Дифференцирующее звено на базе операционного усилителя

Коэффициент передачи для такой электрической схемы определяется

выражением:
K = R1C1.	(6.46)

Выходная величина звена пропорциональна скорости изменения входной величины.

Графики ЛАЧХ и ЛФЧХ при изменении ω от 0 до 10 C−1 и значении K = 3, изображены на рис. 6.13.

Рисунок 6.13 - ЛАЧХ и ЛФЧХ дифференцирующего звена
Частотные функции звена:
W (Iω) = IωK .	(6.48)

U(ω) = 0.

V (ω) = ωK .

A(ω ) = 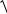U (ω)2 + V (ω)2 = ωK .

V (ω)

ϕ(ω) = arctg = arctg (∞)

U (ω)

			(6.49)
			(6.50)
			(6.51)
=	π	.	(6.52)
=		.	(6.52)

L(ω) = 20lg A(ω) = 20lgωK = 20lg K + 20lgω

(6.53)

L(ω) представляет собой прямую, имеющую наклон плюс 20 дБ/дек. Действительно, при увеличении ω на декаду, т.е. в десять раз,

L10(ω) = 20lg ( K ) + 20lg (10ω ) = 20lg ( K ) + 20lg(ω ) + 20lg(10) . Таким образом, величина L10(ω) увеличилась на 20lg(10) , т.е. на

20 дБ.

Запаздывание по фазе выходного сигнала ϕ(ω) = π .

Как передаточная функция, так соответственно и частотные характеристики дифференцирующего звена зеркально отражают передаточную функцию и соответствующие частотные характеристики интегрирующего звена.

Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена. На практике используют реальные дифференцирующие звенья, обладающие инерционностью, вследствие чего осуществляемое ими дифференцирование является приближенным. Передаточная функция такого звена:

W ( S) =	KS	(6.54)
	.

TS +1

При достаточно малых T звено можно рассматривать как идеальное дифференцирующее.

6.5. Звено чистого запаздывания

Это звено без искажения воспроизводит на выходе входную величину, как идеальное пропорциональное звено, но с той разницей, что выходная

величина запаздывает относительно входной на постоянное время. Уравнение звена чистого запаздывания имеет вид:

y (t ) = x (t −τ ) ,									(6.55)
где τ - время запаздывания.
Передаточная функция звена
W ( S) = E−τS .									(6.56)
Частотные функции звена:
W (Iω ) = E−Iωτ = COS (ωτ ) − I SIN (ωτ ).									(6.57)
U (ω ) = cos(ωτ ) .									(6.58)
V(ω ) = −SIN (ωτ ) .									(6.59)

		2			2				(6.60)
A(ω ) = U(ω) +V (ω) = 1.									(6.60)
A(ω ) = U(ω) +V (ω) = 1.
ϕ(ω) = arctg		V (ω)		= arctg − TAN		(	ωτ	= −ωτ .	(6.61)
ϕ(ω) = arctg				= arctg − TAN			ωτ	= −ωτ .	(6.61)
								)
	U		(ω)
L(ω) = 20lg A(ω) = 0 .									(6.62)

По существу это звено относится к нелинейным. Однако при расчетах САУ с такими звеньями можно применять методы теории линейных систем. Поэтому часто элементы, закон движения которых мало изучен или трудно представим в аналитической форме, после некоторой идеализации представляются в виде звеньев запаздывания.

6.6.Звено второго порядка

6.6.1.Характеристики звена второго порядка

Рассмотрим звено, описываемое дифференциальным уравнением второго порядка:

2 d 2 y (t )						dy (t )		+ y (t ) = Kx(t ) .	(6.63)
T2				+ T1
T2	dt	2		+ T1		dt
						dt

Передаточная функция звена:
W ( s) =					K		.
W ( s) =			T 2s				.		(6.64)
			T 2s		2 +T s+1				(6.64)
		2				1

Обозначим T = T2, ξ =	T1	=	T1	. Тогда передаточная функция звена
	2T2
			2T
запишется в виде:

W (S) =

(6.65)

T 2S2 +2ξTS+1

Характеристическое уравнение:

T2λ2 + 2ξTλ +1 = 0 .

(6.66)

Корни уравнения:

−2ξT± 4ξ 2T2 −4T2

ξ 2 −1

(6.67)

λ1,2 =

2T2

= − T ±

T .

Переходная составляющая имеет вид:

yпер (t ) = C1eλ1t + C2eλ2t .

(6.68)

При положительных действительных корнях характеристического

уравнения lim

yпер (t ) = ∞. Подобная система неработоспособна.

t→∞

При отрицательных действительных корнях переходной процесс затухает и не имеет колебаний. В этом случае передаточная функция (6.64) представляет собой апериодическое звено второго порядка:

W ( S)

(6.69)

(1+λ1S)(1+λ2S)

X(S)

Y(S)

1+λ1S

1+λ2S

Рисунок 6.14 - Апериодическое звено второго порядка

Если

0 < ξ <1, то

корни

характеристического уравнения будут

комплексными:

λ1,2

= −

± I

1−ξ 2

= α + Iβ .

(6.70)

Переходная составляющая yпер (t) в этом случае равна:

yпер (t ) = C1e(α +iβ )t + C2e(α −iβ )t .

(6.71)

Комплексные корни характеристического уравнения определяют колебания в переходной составляющей. Если вещественные части корней будут отрицательными, то колебания будут затухать, если положительными - будут расходиться.

Запишем, не приводя вывода, переходную функцию колебательного звена (корни характеристического уравнения комплексные) при подаче на вход единичного ступенчатого влияния:

	− e−αt					(6.72)
y(t) = K 1	− e−αt	COS βt + α SIN βt .				(6.72)
			β
На рис. 6.15 показан график переходной характеристики для значений
K = 2, T = 1.414 , ξ = 0.354 (α = 0.25 , β = 0.66).
2.5
y (t )
2
1.5
				K	10	(T )
1					10	(T )
1
0.5
0
						T
0		10	20	30		40

Рисунок 6.15 - Переходная характеристика колебательного звена

Графики ЛАЧХ и ЛФЧХ при изменении ω от 0 до 10 C−1 и значениях K = 2, T = 1.414 , ξ = 0.354, показаны на рис. 6.16.

Рисунок 6.16 - Графики ЛАЧХ и ЛФЧХ колебательного звена Из графиков рис. 6.16 следует, что система устойчива, наблюдаются

затухающие колебания, запас по фазе равен 35О. Частотные функции звена:

W (Iω ) =

T 2(Iω )2 +2ξTIω+1 −T 2ω2 +2ξTIω+1

= K

1− T 2ω2 − I2ξTω

(1− T 2ω2 + I2ξTω )(1− T 2ω2 − I2ξTω )

= K

1− T 2ω2

− IK

2ξTω

(1− T 2ω2 )2

+ (2ξTω )2

(1− T 2ω2 )2

+ (2ξTω )2

(6.73)

U (ω ) = K

1−T 2ω2

(1−T 2ω2 )2

+ (2ξTω )2

(6.74)

<<< < Предыдущая 1 2 3 4 56 / 156 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.05.2019390.14 Кб41128_сем 4_4.doc
#
12.02.201620.05 Mб271332231791.pdf
#
12.08.2019202.75 Кб31376_сем 5.doc
#
22.08.20193.96 Mб2137854.rtf
#
12.02.2016420.81 Кб1914_08_18_ТАУ_1,2_Лабораторный практикум.pdf
#
12.02.20165.42 Mб3814_08_18_ТАУ_1,2_Лекционный курс.pdf
#
12.02.20161.03 Mб2414_10_16_ТАУ_1,2_Лабораторный практикум.doc
#
12.02.20167.69 Mб105914_10_25_ТАУ_1,2_Лекционный курс.doc
#
26.08.2019194.05 Кб181_1 Функциональные схемы автоматизации.doc
#
17.11.201885.5 Кб51_8_10_2007 (4).doc
#
12.02.2016163.84 Кб141_chast.doc