
14_08_18_ТАУ_1,2_Лекционный курс
.pdf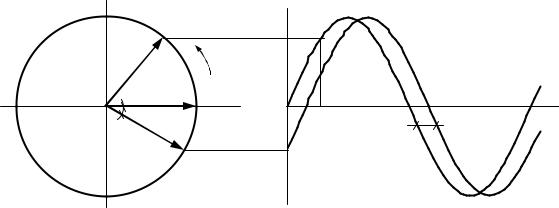
выходе звена к комплексной амплитуде сигнала на его входе, при подаче на вход синусоидального сигнала. Это отношение определяется после окончания переходного процесса, вызванного подачей входного воздействия [2].
Геометрическое место конца вектора комплексного коэффициента усиления звена, при изменении частоты от нуля до бесконечности, называется частотным годографом комплексного коэффициента усиления или комплексной частотной характеристикой звена (рис. 3.5). Иногда комплексную частотную характеристику называют амплитудно-фазовой характеристикой (АФХ).
Объясним переход от записи гармонического сигнала в тригонометрическом виде к комплексной форме. Изобразим на комплексной
плоскости векторы ɺвх и ɺвых , сдвинутые один относительно одного на угол
A A
ϕ (рис. 3.6). Будем поворачивать векторы с частотой ω против часовой стрелки вокруг центра.
IM |
|
|
|
|
x = Aвх SIN (ωt ) |
. |
ωT1 |
|
|
|
|
|
|
|
|
y = Авых SIN (ωt +ϕ) |
|
Авх |
ω |
|
|
||
|
. |
|
|
|
|
|
Авх |
T = 0 |
|
|
|
ϕ |
|
RE |
0 |
ωT1 |
ωT |
|
|
|
|
ϕ |
|
|
. |
|
|
|
|
|
Авых T = 0 |
|
|
|
|
|
|
|
|
ɺ |
ɺ |
Рисунок 3.6 - Проекции векторов Aвх и |
Aвых |
||||
Рядом построим график изменения проекций этих векторов на |
|||||
вертикальную ось во времени T . |
|
|
|
||
Эти графики представляют зависимости: |
|
||||
|
x = Aвх SIN(ωt) |
|
(3.3) |
|
{y = Авых SIN(ωt + ϕ) , |
|
|
|
|
|
|
|
ɺ |
|
ɺ |
где Aвх - модуль вектора Aвх , Aвых - модуль вектора Aвых . |
|||
|
Таким образом, существует однозначная связь гармонических колебаний |
||
X(T ) |
ɺ |
и |
ɺ |
и y(t) с векторами Aвх |
Aвых , расположенными на комплексной |
||
плоскости.
Вектор ɺвх при его вращении описывается уравнением:
A
21

ɺ |
|
|
|
|
|
|
|
|
|
|
|
|
iωt |
. |
|
|
|
|
(3.4) |
||
Aвх = |
Aвх (COSωt + i SIN ωt) = Aвхe |
|
|
|
|
|
|
||||||||||||||
Вектор |
ɺ |
|
|
|
|
|
|
|
|
|
|
|
|
по отношению к вектору |
ɺ |
||||||
Aвых , сдвинутый на угол |
ϕ |
Aвх , |
|||||||||||||||||||
определится как: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ɺ |
|
= A |
COS |
ωt + ϕ |
) |
+ i SIN |
( |
ωt |
+ ϕ |
= A e |
i(ωt+ϕ) |
. |
(3.5) |
||||||||
A |
|
||||||||||||||||||||
|
вых |
|
вых |
|
|
( |
|
|
|
|
|
|
|
) |
вых |
|
|
|
|||
Определим частотную функцию (комплексный коэффициент усиления) |
|||||||||||||||||||||
W (Iω) как отношение выходного сигнала y(t) к входному сигналу X(T ) : |
|
||||||||||||||||||||
|
|
|
y(t ) |
|
|
ɺ |
|
|
|
|
Авых e |
i(ωt +ϕ ) |
= A(ω )eiϕ (ω ) = |
|
|||||||
W ( jω ) = |
|
= |
Aвых |
|
= |
|
|
|
|
||||||||||||
|
ɺ |
Aвх eiω t |
|
|
|||||||||||||||||
|
|
|
x(t ) |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
Aвх |
|
|
|
|
|
|
|
||||||||
|
|
= U (ω) + IV (ω) , |
|
|
|
|
|
|
|
|
|
|
|
(3.6) |
|||||||
где A(ω ), ϕ (ω ) - соответственно, модуль |
и фаза |
комплексной частотной |
|||||||||||||||||||
функции (комплексного коэффициента усиления); U (ω), V (ω) -
соответственно, действительная и мнимая части комплексной частотной функции (комплексного коэффициента усиления).
Модуль A(ω ) |
и фаза ϕ (ω ) частотной функции связаны с |
||||||
действительной U(ω) и мнимой V (ω ) частями следующими выражениями: |
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
(3.7) |
A(ω) = U (ω) |
+V (ω) |
|
, |
||||
|
|
||||||
ϕ (ω ) = arctg |
V |
(ω ) |
|
|
|
||
|
|
. |
|
|
(3.8) |
||
|
|
|
|
||||
|
U |
(ω ) |
|
|
|
||
На комплексной плоскости (рис. 3.7) частотную передаточную функцию определяет годограф вектора OA , длина (модуль) которого равна A(ω) , а аргумент (угол, образованный этим вектором с действительной положительной полуосью) равен ϕ(ω) . Кривую, которую описывает конец вектора при изменении частоты от 0 до ∞ , называют амплитудно-фазовой характеристикой (АФХ). Таким образом, АФХ – это совмещённые АЧХ и ФЧХ.
22

Рисунок 3.7 - Построение АФХ по частотной функции Итак, передаточная функция полностью определяет как статические, так и
динамические свойства системы (звена). Она показывает, по какому закону тот или иной сигнал, поступивший на вход, преобразуется в выходной сигнал системы или звена.
Рассмотрим получение АЧХ и ФЧХ на примере апериодического звена с передаточной функцией:
W (S) = |
K |
(3.9) |
. |
TS +1
Частотную функцию (комплексный коэффициент усиления) получим, заменив в уравнении (3.9) S на Iω :
W (Iω) = W (S) |
|
S=Iω = |
K |
|
|
. |
|
|
|
(3.10) |
|||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
|
TIω +1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Выделим из частотной функции W (Iω) действительную U(ω) и |
|||||||||||||||||
мнимую V (ω) части: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
K |
|
|
|
|
|
K |
|
|
|
KTω |
|
|
|
|||
|
|
complex → |
|
|
|
|
− i |
|
|
, |
(3.11) |
||||||
|
|
|
|
|
|
|
|
||||||||||
|
Tiω +1 |
|
|
|
2 |
2 |
|
|
2 |
2 |
|
|
|||||
|
|
|
|
1+ T ω |
|
|
|
1 + T ω |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
U(ω) = |
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
, |
|
|
|
|
|
|
|
|
|
(3.12) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 + T 2ω2 |
|
|
|
|
|
|
|
|
|
|
|||||
V (ω) = − |
KTω |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
. |
|
|
|
|
|
|
|
(3.13) |
|||||
|
|
2ω2 |
|
|
|
|
|
|
|
||||||||
|
|
|
1 + T |
|
|
|
|
|
|
|
|
|
|
|
|||
Амплитудно-частотная А(ω) характеристика:
23
А(ω) = U(ω)2 +V (ω)2 = |
|
K |
||
|
|
|
. |
|
|
|
|
||
|
||||
|
1 + T 2ω2 |
|||
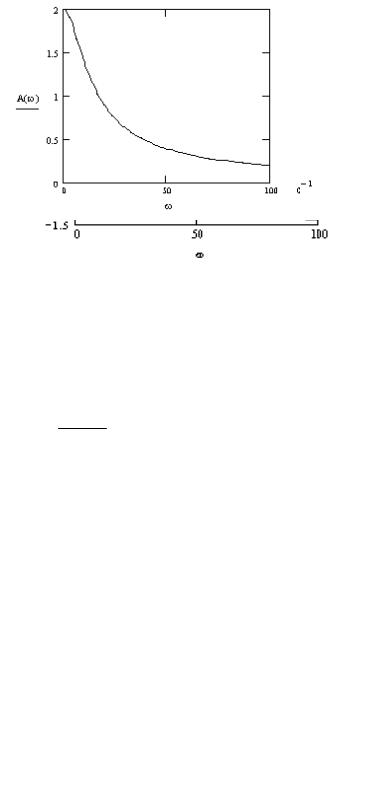
График АЧХ при изменении ω от 0 до 100 1/с и значениях T = 0.1 с, изображен на рис. 3.8.
Рисунок 3.8 - График АЧХ Фазовая частотная характеристика:
V (ω)
ϕ(ω) = arctg = −arctg (Tω ) .
U (ω)
График ФЧХ при изменении ω от 0 до 100 1/с и значениях T = 0.1 с, показан на рис. 3.9.
(3.14)
K = 2,
(3.15)
K = 2,
Рисунок 3.9 - График фазовой частотной характеристики В практических расчетах амплитудную и фазовую частотные
характеристики чаще всего изображают в логарифмическом масштабе, что позволяет в значительной степени упростить анализ и синтез САУ.
Коэффициент усиления в логарифмическом масштабе измеряется в децибелах. Понятие децибела введено в практику компанией Bell Telephone
24

Labs в двадцатых годах двадцатого столетия. Сначала оно применялось для измерения логарифма отношения мощностей электрических сигналов:
P
X =10 × lg 1 , дБ, (3.16)
P2
где Р1, Р2 - мощности электрических сигналов.
Поскольку мощность пропорциональна квадрату напряжения, то для гармонического сигнала можно записать:
2 |
(3.17) |
|
P ≡ U . |
||
|
Поэтому в логарифмическом масштабе коэффициент усиления по напряжению, измеренный в децибелах, будет равен:
|
P |
|
U |
2 |
U |
|
||
10 × lg |
1 |
= 10 × lg |
1 |
|
= 20 × lg |
1 |
. |
(3.18) |
|
|
|
||||||
|
P2 |
U2 |
|
|
U2 |
|
||
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ), выраженная в децибелах, соответствующая амплитудно-частотной характеристике (3.14) определится:
L(ω) = 20lg A(ω) = 20lg |
|
|
K |
|
|
|
||||
|
|
|
|
. |
|
(3.19) |
||||
|
|
|
|
|
||||||
|
|
|||||||||
|
|
|
|
1 + T 2ω2 |
|
|
|
|||
Фазовая |
частотная |
характеристика |
ϕ (ω ) , |
построенная |
в |
|||||
полулогарифмическом масштабе |
(по оси ординат откладывается угол ϕ |
в |
||||||||
градусах или радианах, по оси абсцисс - lg (ω) ), называется логарифмической
фазовой частотной характеристикой (ЛФЧХ).
Вкачестве единицы измерения частоты используется логарифмическая единица - декада. Декадой называется интервал частот между какой-либо величиной частоты и ее десятикратным значением.
Влогарифмическом масштабе частот отрезок в одну декаду не зависит от частоты и имеет длину, равную:
lg(10ω ) − lg(ω ) = lg(10) + lg (ω ) − lg(ω ) = lg (10) = 1.
ЛАЧХ и ЛФЧХ строят обычно совместно, используя общую ось абсцисс (ось частот). Начало координат невозможно установить в точке ω = 0, так как lg (0) = −∞. Поэтому начало координат располагают в любой удобной точке в
зависимости от интересующего диапазона частот.
Соответствующие графики ЛАЧХ и ЛФЧХ изображены на рис. 3.10.
25

Рисунок 3.10 - График ЛАЧХ и ЛФЧК (диаграмма Боде)
4.Показатели качества систем автоматического управления
4.1.Оценка качества регулирования при стандартных воздействиях
Кпроцессам управления предъявляются три основных требования: по точности в установившемся режиме, по устойчивости и по качеству переходных процессов.
Основной задачей управления является обеспечение качества работы системы при известных возмущениях, управляющих воздействиях и заданных ограничениях на параметры системы.
Качество управления - это комплекс требований, которые определяют поведение системы в установившемся и переходном режимах отработки управляющего воздействия.
В теории автоматического управления решаются, в основном, две задачи.
•Задача анализа (исследования) системы - установить, какое влияние оказывает структура системы и значения ее параметров на процесс управления и показатели его качества, а также выяснить, насколько та или другая система соответствуют предъявляемым к ней требованиям.
26

•Задача синтеза системы - выбор структуры и параметров системы управления в соответствии с требованиями качества.
В большинстве случаев исследования проводятся при подаче на вход системы типовых воздействий. К ним относятся единичное ступенчатое воздействие и гармонический сигнал.
Единичное воздействие (рис. 4.1) - функция, которая принимает значение 1 при значениях времени T ≥0, в других случаях эта функция равняется 0:
|
|
|
t ≥ 0 . |
|
|
10 |
(t ) = 1 |
при |
(4.1) |
||
|
0 |
|
t < |
0 |
|
|
|
при |
|
|
|
10 (T )
1
t
Рисунок 4.1 - Единичный ступенчатый сигнал Для определения полосы частот пропускания в качестве входного
управляющего воздействия используют гармонический сигнал: |
|
X = ASIN (ωT + ϕ ) , |
(4.2) |
где A - амплитуда; ω - угловая частота, ϕ - начальная фаза.
Рассмотрим показатели качества переходного процесса. Переходная характеристика системы y(t) , которая является реакцией системы на единичный сигнал 10(t) , изображена на рис. 4.2.
27

|
σдин |
|
|
|
|
max |
|
y (t ) |
|
|
σуст |
|
|
|
|
10 (T ) |
|
|
|
|
σдин |
2 |
з |
|
|
|
yуст |
|
N = 2 |
|
|
tн |
tм |
t p |
t |
|
|||
Рисунок 4.2 - Показатели качества системы автоматического управления |
|||
Основные показатели качества.
•tн - время первого достижения установившегося значения.
•tм - время достижения первого максимума.
•yуст - установившееся значение выходного сигнала, определяющее
статическую точность системы.
•Статическая ошибка системы (установившееся рассогласование), показывает, насколько значение выходного сигнала отличается от заданной величины
σ |
уст |
= lim 1 (t) − y |
( |
t |
|
, |
(4.3) |
|
|
t→∞ |
0 |
|
) |
|
|||
|
|
|
|
|
|
|
|
|
•Время регулирования t р - основная характеристика быстродействия системы, определяемая из условия:
10 (t) − y (t ) |
≤ |
з при t ≥ t p , |
(4.4) |
|
где |
з = 0.05 |
– заданное значение, определяемое |
точностью |
|
системы. |
|
|
||
•Динамическое отклонение σдин - характеризует плавность протекания переходного процесса. Определяется как отклонение выходного сигнала y(t) от заданного значения выходной величины в местах перегиба графика переходного процесса.
•Максимальное динамическое отклонение σдинmax - наибольшее значение из всех динамических отклонений.
28

•Перерегулирование - безразмерная величина, определяемая как отношение максимального динамического отклонения к установившемуся значению, взятое в процентах:
|
σдин |
|
δ = |
max 100%. |
(4.5) |
yуст
•Колебательность N - число динамических отклонений за время регулирования t p .
В качестве примера рассмотрим звено с передаточной функцией
3
W (S) = . Переходная характеристика этого звена изображена на
2S2 + 0.5S +1
рис. 4.3.
5 |
|
|
|
|
|
|
|
y(t) 1 |
σдин |
= 1.62 |
δ = 54% |
|
|
||
4 |
|
|
|||||
max |
|
|
|
|
|
σуст = 0 |
|
|
3 |
5 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
yуст |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
10 |
20 |
30 |
t |
p |
40 |
t |
|
50 |
||||||
Рисунок 4.3 - Переходная характеристика колебательного звена Определим по переходной характеристике показатели качества
переходного процесса:
•установившаяся ошибка - σуст = 0.
•время регулирования - t p = 34 с .
•максимальное динамическое отклонение - σдинmax = 1.62.
•перерегулирование - δ = 1.62 100% = 54% .
3
• колебательность - N = 6.
29

4.2. Корневые критерии качества
Эта группа критериев базируется на оценке качества переходных процессов по значению полюсов и нулей передаточной функции системы, путем анализа корней ее знаменателя и числителя.
Передаточная функция системы связывает изображение выходной и входной величин зависимостью:
W ( S) = |
B( S) |
|
||
|
|
, |
(4.6) |
|
|
|
|||
|
A( S) |
|
||
где B( S) = BMSM + BM−1S M−1+... + BO , A( S ) = ANSN + AN−1SN−1 + ... + AO . |
||||
Разложив |
многочлены в |
числителе и знаменателе на множители, |
||
передаточную функцию системы можно представить в виде:
m
bo ∏ (s − λoi )
W ( s) = |
i=1 |
, |
(4.7) |
|
n
ao ∏ (s − λпi ) i=1
где λoi - нули передаточной функции, λпi - полюсы передаточной функции. Нули и полюсы передаточной функции определяют качественные
показатели переходного процесса [3].
В частном случае, когда передаточная функция не имеет нулей:
W ( s) = |
bo |
, |
|
n |
|||
|
(4.8) |
||
|
ao ∏ (s − λпi ) |
||
|
|
||
|
i=1 |
|
качество переходного процесса определяется только полюсами передаточной функции.
Из теории линейных дифференциальных уравнений известно, что общее решение уравнения (4.8) имеет вид:
n |
|
y (t ) = ∑ Cieλпit , |
(4.9) |
i=1 |
|
где Ci - константа, зависящая от начальных условий; λпi |
- корни знаменателя |
уравнения (4.8). |
|
30
