
14_08_18_ТАУ_1,2_Лекционный курс
.pdf
Разомкнутый контур регулирования - контур, в котором последовательно соединены звенья, которые находятся в прямом канале регулирования и в канале обратной связи (рис. 5.8).
x(s) |
|
|
|
|
|
xос(s) |
W1(s) |
|
W2(S) |
Wос (s) |
|||
|
|
|
|
|||
|
|
|
|
|
|
|
Рисунок 5.8 - Разомкнутый контур регулирования Если сигнал задания суммируется с сигналом обратной связи, то такая
связь называется положительной, если из сигнала задания вычитается сигнал обратной связи, то такая связь называется отрицательной.
Правило преобразования:
Эквивалентная передаточная функция замкнутой системы записывается как дробь: в числителе дроби находится перемножение передаточных функций прямого канала регулирования, в знаменателе дроби - единица плюс (минус) перемножения передаточных функций разомкнутого контура.
5.2.4. Перенос звеньев
При преобразовании структурных схем иногда необходимо переносить звенья через узел разветвления, как в направлении передачи сигнала, так и в противоположном направлении.
Рассмотрим перенесение звена через узел разветвления по направлению передачи сигнала (рис. 5.9).
x(s) |
|
X1(S) |
x(s) |
|
X1(S) |
|
W1(s) |
W1(s) |
|||||
|
|
|
|
|||
|
|
|
|
|
|
W1(s)
 X1(S)
X1(S)
Рисунок 5.9 - Перенос звена через узел разветвления по направлению передачи сигнала
При такой операции в цепи добавляют фиктивные звенья с передаточной функцией перенесенного звена.
41

При перенесении звена через узел разветвления в направлении обратном передаче сигнала (рис. 5.10) в цепь добавляют фиктивное звено с передаточной функцией обратной передаточной функции звена, через которое выполнен перенос.
x(s) |
|
X1(S) |
x(s) |
|
X1(S) |
|
W1(s) |
W1(s) |
|||||
|
|
|
|
|||
|
|
|
|
|
|
x(s)
1
W1(S)
X1(S)
Рисунок 5.10 - Перенос звена через узел разветвления в направлении обратном передаче сигнала
6. Типовые звенья систем автоматического управления
Объекты в теории автоматического управления описываются передаточными функциями, содержащими полиномы от S произвольного порядка в числителе и знаменателе. Но, если передаточная функция объекта содержит только простой множитель в числителе, либо в знаменателе, то объект называется типовым динамическим звеном (типовым звеном).
Из курса алгебры известно, что полином любого порядка можно разложить на простые множители. То есть любую САУ можно представить в виде последовательного соединения типовых звеньев. С другой стороны, реальные звенья САУ могут иметь самую разнообразную физическую основу (электронные, механические, гидравлические, электромеханические и т.п.) и конструктивное выполнение, но иметь одинаковые передаточные функции и являться одинаковыми типовыми звеньями. Поэтому знание характеристик звеньев столь же необходимо для расчетов САУ, как знание таблицы умножения в арифметике.
Все линейные типовые звенья разделяют на три основных группы:
позиционные звенья,
интегрирующие звенья,
дифференцирующие звенья.
42
Позиционные звенья: апериодическое, пропорциональное, колебательное, консервативное и чистого запаздывания - характеризуется тем, что в каждом из них, кроме консервативного, при подаче на вход постоянной величины с течением времени устанавливается постоянное значение выходной величины.
В интегрирующих звеньях при постоянном входном воздействии выходная величина неограниченно растет.
Дифференцирующие звенья характеризуются тем, что реагируют только на изменение входной величины.
Рассмотрим типовые звенья и их характеристики.
6.1. Апериодическое звено первого порядка 6.1.1. Характеристики звена первого порядка
Динамические процессы в звеньях первого порядка описываются дифференциальными уравнениями первого порядка:
T |
dy(t) |
|
+ y(t) = Kx(t) . |
(6.1) |
||
dt |
||||||
|
|
|
|
|
||
Передаточная функция апериодического звена первого порядка (6.1) |
||||||
после преобразования Лапласа имеет вид: |
|
|||||
W (S) = |
|
K |
(6.2) |
|||
|
|
. |
||||
|
||||||
|
|
|
TS +1 |
|
||
Решение уравнения (6.1) можно записать в виде [4]: |
|
|||||
y(t) = yуст + yпер (t) , |
(6.3) |
|||||
где yуст - установившаяся (вынужденная) составляющая; yпер - переходная
составляющая изменения выходной координаты во времени.
Установившаяся составляющая определяется входным сигналом, а переходная - свойствами самой системы. Будем искать общее решение уравнения (6.1) в следующем виде:
yпер (t) = Ceλt , |
(6.4) |
где C и λ - пока неопределенные коэффициенты.
Подставим выражение (6.4) в (6.1). Приравняв правую часть уравнения к нулю, получим:
TλCeλt + Ceλt = 0 , |
(6.5) |
или
43
Ceλt (λT +1) = 0. |
(6.6) |
||
Очевидно, что уравнение выполняется при любых значениях C , если |
|||
1 |
|
|
|
λ = − |
|
. |
|
|
|
||
|
Т |
|
|
Выражение λТ +1 = 0 |
называется характеристическим уравнением |
||
исходного дифференциального уравнения. Если сравнить выражение (λТ +1)
со знаменателем передаточной функции (6.2) (Тs +1) , то видно, что они имеют один и тот же вид. Если в знаменателе передаточной функции подставить λ взамен S и приравнять это выражение к нулю, то получим характеристическое
уравнение: |
|
Тλ +1 = 0. |
(6.7) |
Таким образом, переходная составляющая дифференциального уравнения |
|
(6.1) имеет вид: |
|
|
|
|
|
|
|
t |
|
|
|
|
|
(6.8) |
||
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
y(t) = Ce |
T . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||
Решим дифференциальное уравнение (6.1) при входном сигнале в виде |
||||||||||||||
единичного ступенчатого скачка: |
|
|||||||||||||
x(t) = 10(t) , |
|
|
|
|
|
(6.9) |
||||||||
T |
dy(t) |
+ y(t) = K10(t) . |
|
(6.10) |
||||||||||
|
|
|||||||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
||
Постоянное значение yуст определяется для значений времени T → ∞. |
||||||||||||||
Переходная составляющая yпер стремится к нулю, так как |
|
|||||||||||||
|
|
|
|
|
|
|
− |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
y |
|
|
(∞) |
= Ce T |
= |
= 0 . |
|
|||||||
пер |
|
|
|
(6.11) |
||||||||||
|
∞ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eT |
|
|
||
В этом случае, согласно уравнению (6.3), установившееся |
значение |
|||||||||||||
yуст = y(t) и равняется K10(T). |
|
|||||||||||||
Запишем выражение (6.3) в виде:
t
− |
|
|
(6.12) |
|
|
||||
y(t) = K1 (t) + Ce T . |
||||
|
||||
0 |
|
|
|
|
44
Найдем значение коэффициента |
C при нулевых начальных условиях |
||||||
|
T |
|
|
|
|
||
− |
|
|
|
|
|
|
|
T =1. Тогда уравнение (6.12) имеет вид: |
|||||||
T = 0, y(t) = 0 , E |
|||||||
0 = K + C . |
|
|
|
|
|
(6.13) |
|
Отсюда определим C : |
|
|
|||||
C = −K . |
|
|
|
|
|
(6.14) |
|
Окончательно уравнение (6.3) запишется: |
|||||||
|
|
|
− |
t |
|
|
|
h(t) = y(t) = |
|
|
|
|
|
||
|
|
|
|
||||
K 1 − e |
|
T |
. |
(6.15) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
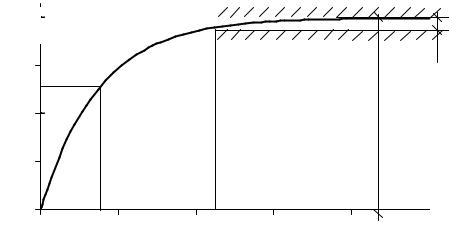
На рис. 6.1 показанный график переходной характеристики для значений |
|||||||
K = 2, T = 3. |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
H(2) |
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
0.05 yуст |
0.67 yуст |
|
|
|
10 (T ) |
|
|
|
1 |
|
|
|
|
|
|
|
0.5 |
|
|
|
|
y |
уст |
= K10 (t) |
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
T 4 |
|
tp |
|
|
T |
|
0 |
8 |
12 |
16 |
20 |
|
||
Рисунок 6.1 - Переходная характеристика апериодического звена первого порядка
Рассмотрим характерные точки на переходной характеристике, которые
определяют показатели качества. |
|
Время регулирования tр определяется |
моментом времени, когда |
значение переходной характеристики попадает |
в «коридор» 0.05yуст и |
больше не выходит за его пределы. Значение |
0.95K достигается за время |
t = 3T . Действительно: |
|
45

−3T
|
|
(6.16) |
|
E T |
|||
= 0.05 . |
|||
Таким образом, продолжительность переходного процесса равняется:
t р = 3T . |
(6.17) |
Коэффициент T называется постоянной времени. |
|
Если на графике переходного процесса из точки |
Y = 0.67K опустить |
перпендикуляр на ось времени, то полученное значение будет численно равно постоянной времени T. Действительно:
|
−T |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
H (T ) = K 1 |
− E T |
|
= K 1 |
− |
|
|
= 0.67K . |
(6.18) |
|
||||||||
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
Переходная характеристика апериодического звена (рис. 6.1) не имеет колебаний, и его параметры определяются коэффициентом усиления (передачи)
Kи постоянной времени T.
6.1.2.Частотные характеристики звена первого порядка
Комплексный коэффициент усиления для передаточной функции (6.2) определяется как:
W (Iω) = |
K |
(6.19) |
. |
TIω +1
Для построения графика комплексного коэффициента усиления воспользуемся пакетом Matlab [3]. Зададим передаточную функцию (6.19), введя в командной строке следующую запись H = TF ([K], [T 1]) . При правильной записи на экране появится передаточная функция указанного звена. После этого набираем команду nyquist (H). График комплексного коэффициента усиления будет изображен в отдельном окне. Чтобы не показывать на графике отрицательные частоты надо в контекстном меню выбрать пункты SHOW, Negative Frequencies .
Для значений K = 4, T = 0.1 с график АФХ представлен на рис. 6.2.
46

Рисунок 6.2 - Частотный годограф комплексного коэффициента усиления (диаграмма Найквиста)
|
K |
||
АФХ представляет собой полуокружность с радиусом |
|
в четвертом |
|
2 |
|||
|
|
||
|
K |
|
|
|
квадранте комплексной плоскости и центром в точке |
|
|
,I0 |
на |
|
||||
|
2 |
|
|
|
действительной оси.
Для построения логарифмической амплитудно-частотной и логарифмической фазовой частотной характеристик введем команду
MARGIN(H) .
Для значений K = 4, T = 0.1 с в пакете Matlab будут построены ЛАЧХ и ЛФЧХ (рис. 6.3).
47

Рисунок 6.3 - Графики ЛАЧХ и ЛФЧХ ЛАЧХ в соответствии с уравнением (3.19):
L(ω) = 20lg A(ω) = 20lg |
|
K |
|
|
|
|
|
|
|
||||
|
|
|
|
. |
|
|
(6.20) |
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
||||||||||
|
|
|
|
|
1+ T 2ω2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
При нулевой частоте |
|
ω = 0 получим |
значение, |
соответствующее |
|||||||||
установившемуся режиму: |
|
|
|
|
|
|
|
|
|
|
|
||
L(0) = 20lg |
|
K |
|
= 20lg K = |
20lg 4 =12.04 . |
|
|
||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||
1 + T 202 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|||||||||||
При больших частотах (Tω)2 >>1. В этом случае (Tω)2 +1 ≈ Tω . |
|||||||||||||
Выражение для ЛАЧХ приобретает вид: |
|
|
|
|
|||||||||
L(ω) = 20lg ( K ) − 20lg (Tω) . |
|
|
|
|
|
(6.21) |
|||||||
В этом случае L(ω) |
представляет |
|
собой |
прямую, |
имеющую наклон |
||||||||
минус 20 дБ/дек. Действительно, при увеличении ω на декаду, т.е. в десять раз,
L10(ω) = 20lg ( K ) − 20lg (T ×10ω) = 20lg ( K ) − 20lg (Tω) − 20lg (10) . Таким образом, величина L10(ω) уменьшилась на 20lg(10) , т.е. на
20 дБ.
48

ЛФЧХ описывается уравнением (3.15): |
|
|
|
|
|
|
||
ϕ(ω) = −arctg (Tω ) . |
|
|
|
(6.22) |
||||
При ω → ∞ значение ϕ изменяется от 0 |
|
π |
1 |
|
||||
до − |
|
. В точке |
ω = |
|
|
|||
|
|
|||||||
|
|
|
2 |
|
|
T |
||
|
π |
|
|
|
|
|
|
|
фазовый сдвиг приобретает значение ϕ = − |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
|
|
|
|
|
|
|
|
Для получения АЧХ и ФЧХ надо из контекстного меню выбрать пункт Properties . Открыть вкладку UNITS (рис. 6.4). Свойства осей следует перевести из логарифмического масштаба в обычный масштаб, как показано на рис. 6.4, а, б.
а – логарифмический масштаб осей б – обычный масштаб осей Рисунок 6.4 - Вкладка UNITS
После изменения масштаба осей на графиках будут изображены АЧХ и ФЧХ для значений K = 4, T = 0.1 (рис. 6.5).
49

Рисунок 6.5 - Графики АЧХ и ФЧХ
6.2. Пропорциональное звено
Выходная величина этого звена пропорциональная входной величине X . Уравнение звена:
Y = KX , |
(6.23) |
где K - коэффициент усиления звена. |
|
Передаточная функция звена |
|
W ( S) = K . |
(6.24) |
Примером такого звена является усилитель постоянного тока (рис. 6.7).
|
|
R2 |
X |
R1 |
Y |
|
|
|
|
|
Д1 |
Рисунок 6.7 - Усилитель на базе операционного усилителя Коэффициент усиления K равняется:
50
