Файловый архив студентов. Файловый архив студентов.
1306 вузов, 5172 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Запорожский национальный технический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

big_doc_LKG

.pdf
Скачиваний:
18
Добавлен:
07.02.2016
Размер:
20.24 Mб
Скачать
☆

378

Розділ 8

– середнє значення функції відгуку , отримане за результатами

паралельних дослідів.

В табл. 8.1 представлена матриця планування експериментів для двох незалежних факторів.

Таблиця 8.1 Матриця планування ПФЕ типу 22

№

 

Фактори

 

Функція

досліду

 

 

 

 

 

відгуку

 

 

 

 

 

 

 

 

 

 

 

 

1

+1

 

–1

 

–1

 

2

+1

 

+1

 

–1

 

3

+1

 

–1

 

+1

 

4

+1

 

+1

 

+1

 

 

 

 

 

 

 

 

Щоб отримати планування 23 для трьох факторів (, , ), необхідно переписати табл. 8.1 ще раз і до неї праворуч приписати ще один стовпець з чотирма знаками мінус і чотирма знаками плюс (табл. 8.2). Рамкою обведені частини матриці, що повторюються.

 

 

 

 

 

Таблиця 8.2

Матриця планування ПФЕ типу 23

 

 

 

 

 

 

 

№

 

 

Фактори

 

Функція

досліду

 

 

 

 

 

відгуку

 

 

 

 

 

 

 

1

+1

 

–1

–1

–1

 

2

+1

+1

–1

–1

 

3

+1

 

–1

+1

–1

 

4

+1

+1

+1

–1

 

5

+1

 

–1

–1

+1

 

6

+1

+1

–1

+1

 

7

+1

 

–1

+1

+1

 

8

+1

+1

+1

+1

 

Те саме виконують, якщо необхідно отримати планування експерименту для чотирьох факторів: матрицю із табл. 8.2 повторюють два

рази і праворуч приписують стовпець з восьми мінусами і восьми плюсами (табл. 8.3).

 

Дослідження систем методом планування експериментів

379

 

 

 

 

 

 

 

 

 

Таблиця 8.3

 

 

 

Матриця планування ПФЕ типу 24

 

 

 

 

 

 

 

 

 

 

 

 

 

 

№

 

 

 

 

Фактори

 

Буквене

 

 

 

 

 

 

 

 

 

позначення

 

 

досліду

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

рядків

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

+1

 

–1

–1

–1

–1

(1)

 

 

2

 

+1

+1

–1

–1

–1

a

 

3

 

+1

 

–1

+1

–1

–1

b

 

4

 

+1

+1

+1

–1

–1

ab

 

5

 

+1

 

–1

–1

+1

–1

c

 

6

 

+1

+1

–1

+1

–1

ac

 

7

 

+1

 

–1

+1

+1

–1

bc

 

8

 

+1

+1

+1

+1

–1

abc

 

9

 

+1

 

–1

–1

–1

–1

d

 

10

 

+1

+1

–1

–1

–1

ad

 

11

 

+1

 

–1

+1

–1

–1

bd

 

12

 

+1

+1

+1

–1

–1

abd

 

13

 

+1

 

–1

–1

+1

–1

cd

 

14

 

+1

+1

–1

+1

–1

acd

 

15

 

+1

 

–1

+1

+1

–1

bcd

 

16

 

+1

+1

+1

+1

–1

abcd

 

У загальному випадку для запису матриці плану довільного ПФЕ можна скористатися простим правилом: у стовпці знаки мінус і плюс чергуються; у стовпці чергуються два мінуси і два плюси; у стовпці чергуються чотири мінуси і чотири плюси; у стовпці чергуються вісім мінусів і вісім плюсів і т.д. з подвоєнням кількості знаків, що чергуються.

Планування можна записати у буквеному позначенні. Для цього позначимо фактори прописними буквами латинського алфавіту (табл. 8.3). Якщо рядок позначений буквою , це означає, що фактор

взятий на верхньому рівні (+1), а решта факторів взяті на нижньому рівні (–1). Якщо рядок позначений буквою , то тільки фактор взятий на верхньому рівні, а решта – на нижньому. Позначення означає, що фактори і взяті на верхньому рівні. Якщо всі фактори взяті на нижньому рівні (як у першому рядку табл. 8.3), то

цей рядок позначають знаком (1).

380

Розділ 8

Як приклад, наведемо буквене позначення розглянутих раніше планів експериментів.

ПФЕ 22: (1), a, b, ab. ПФЕ 23: (1), a, b, ab, c, ac, bc, abc. Плануючи експеримент, на першому етапі прагнуть отримати лі-

нійну модель. Проте, немає гарантії, що у вибраних інтервалах варіювання факторів процес описується моделлю .

Практично виникає необхідність в застосуванні більш складних залежностей для опису функції відгуку. Для цього потрібно, використовуючи правило перемножування стовпців, отримати добутки па-

рних факторів. При обчисленні коефіцієнта, який характеризує ефект взаємодії, з новим вектор-стовпцем можна поводитися так саме, як з вектор-стовпцем будь-якого із факторів. Модель для ПФЕ типу 23 з ефектами взаємодії має такий вигляд

(8.13)

В стовпцях , , задають планування і на їх основі визначають умови дослідів. Інші стовпці , , , використовуються тільки для розрахунку. В табл. 8.4 наведена матриця трифакторного експерименту з урахуванням ефекту взаємодії факторів.

Таблиця 8.4 Матриця планування ПФЕ типу 23 з ефектами взаємодії

№

 

 

 

Фактори і їх комбінації

 

 

 

 

 

 

 

 

 

 

досліду

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

+1

–1

–1

–1

+1

+1

+1

–1

 

2

+1

+1

–1

–1

–1

–1

+1

+1

 

3

+1

–1

+1

–1

–1

+1

–1

+1

 

4

+1

+1

+1

–1

+1

–1

–1

+1

 

5

+1

–1

–1

+1

+1

–1

–1

+1

 

6

+1

+1

–1

+1

–1

+1

–1

–1

 

7

+1

–1

+1

+1

–1

–1

+1

–1

 

8

+1

+1

+1

+1

+1

+1

+1

+1

 

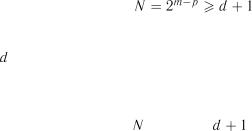
Дослідження систем методом планування експериментів

381

З практичної точки зору ПФЕ має суттєвий недолік: із збільшенням кількості факторів швидко зростає кількість дослідів.

8.4.1.2. Дробовий факторний експеримент (ДФЕ). Плани пов-

ного факторного експерименту стають незручними для викорис-

тання, коли кількість факторів стає значною. Наприклад, при

кількість дослідів у матриці планування становитиме , а при необхідно провести вже досліди, що на практиці може виявитись не реальним. У таких випадках використовують плани експерименту, які включають тільки половину, чверть або восьму частину дослідів, заданих планом повного факторного експеримен-

ту. Такі плани називають дробовими факторними експериментами (ДФЕ). У цих планах кількість спроб менше кількості точок у

факторному просторі.

В основу побудови дробового плану експерименту покладено відповідний повний план експерименту (він виступає як базовий план), який доповнюється стовпцями, що задають комбінації досліджуваних факторів.

Найбільше розповсюдження мають регулярні плани ДФЕ типу . У цьому позначенні для конкретних і віднімання не здійснюється, а зберігаються обидві цифри. Перша цифра характеризує

кількість факторів, а друга – ступінь дробовості ДФЕ. Відповід-

ні плани ДФЕ прийнято називати репліками з зазначенням їх ступені дроблення. Так, план ДФЕ – це 1/2 репліка ПФЕ ; ДФЕ – 1/8 репліка ПФЕ 2m і т. д.

Мінімально припустима ступінь дробовості при заданому списку суттєвих змінних визначається за умови

,

(8.14)

де – кількість дослідів (кількість стовпців);

– загальна кількість коефіцієнтів, що входять в регресійну модель (кількість стовпчиків в матриці планування).

Цією умовою також визначається і загальна кількість рядків в мат-

риці плану ДФЕ.

 

Якщо кількість дослідів дорівнює

(кількості коефіцієнтів в

лінійному рівнянні регресії), то дробова репліка являє собою насиче-

ний лінійний ортогональний план.

382

Розділ 8

На практиці для побудови планів ДФЕ запропонована процедура, яка включає три основні етапи.

Етап 1. Із загальної кількості факторів , , , вибирається провідних (). Для вибраних факторів записується базисний план ПФЕ .

Етап 2. Для решти факторів, які будуть змінюватися в ході експерименту, вибираються стовпці, що відповідають тим чи іншим добуткам провідних факторів. Співвідношення, що прив'язують один із стовпців , , , до стовпця відповідного добутку

якої-небудь комбінації факторів , , , називається генеруючим співвідношенням. Всього повинно бути задано генеруючих співвідношень. Вибір таких співвідношень достатньо довільний. В якості генеруючих можуть застосовуватися добутки факторів , , , , взяті як зі знаком плюс, так і зі знаком мінус. Питання про те, з яким знаком брати той чи інший добуток провідних факторів у генеруючому співвідношенні, вирішується довільно. Після перших

двох етапів побудова плану ДФЕ завершується.

Етап 3. На цьому етапі здійснюється перевірка придатності плану. Якщо в отриманій матриці відсутні повністю співпадаючі або

повністю протилежні стовпці, отриманий план придатний для по-

дальшого експериментування і проблема його визначення враховується вирішеною. Якщо такі стовпці виявлені, слід вибрати інші гене-

руючі співвідношення, а якщо і це не допоможе, то змінити набір провідних факторів. Досі не існує якого-небудь конструктивного алгоритму, що дозволяє за списком суттєвих змінних відразу синтезувати придатний план ДФЕ . Єдиний спосіб отримання такого плану – це зазначений спосіб поступового перебору варіантів доти, доки не буде знайдений придатний.

Вирішення даної задачі ускладнюється ще й тим, що заздалегідь не можна сказати, чи вирішувана вона, тобто, чи можна в принципі за даною ступеню дроблення ДФЕ і зазначеному наборі суттєвих змінних побудувати придатний план. Може виявитися, що розв'язку не існує, і необхідно перейти до репліки меншого дроблення.

Процедуру побудови планів ДФЕ розглянемо на прикладах.

Дослідження систем методом планування експериментів

383

Приклад 1. Маємо список суттєвих змінних: , ,

, . Загальна кількість

елементів у цьому списку

. Отже, для отримання регресійної моделі можна

спробувати використати ДФЕ

, який включає чотири досліди.

 

Вибираємо провідні фактори

і . Для фактора

необхідно зазначити гене-

руюче співвідношення. Тут практично не має інших варіантів, як в якості генеруючого

співвідношення вибрати добуток факторів

і , тобто задати програму зміни фак-

тора

, яка співпадає з тим, як буде змінюватися стовець взаємодії

. Таким чи-

ном,

генеруюче співвідношення запишеться у вигляді

.

 

Розглянемо два плани ДФЕ – з додатним і від'ємним знаками генеруючого співвідношення (табл. 8.5).

 

 

 

 

 

 

 

 

 

 

Таблиця 8.5

 

 

 

 

 

Плани ДФЕ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

№

 

Перший варіант

 

№

 

Другий варіант

дос-

 

 

 

 

 

дос-

 

 

 

 

 

 

 

 

 

 

 

 

 

ліду

 

 

 

 

 

ліду

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

+1

–1

–1

 

+1

1

+1

–1

–1

–1

2

+1

+1

–1

 

–1

2

+1

+1

–1

+1

3

+1

–1

+1

 

–1

3

+1

-1

+1

–1

4

+1

+1

+1

 

+1

4

+1

+1

+1

+1

 

 

 

 

 

 

 

 

 

 

 

Оскільки для обох варіантів всі стовпці різні, то ці плани еквівалентні і придатні для отримання регресійної моделі

.

Припустимо, що список суттєвих змінних складений неправильно і в дійсності на функцію відгуку впливають також і змінні , , , , тобто об’єкт дослідження описується рівнянням

.

Нехай дослідник не знає про це, і, як і раніше, реалізує перший варіант плану ДФЕ із табл. 8.5. В табл. 8.6 наведений план ДФЕ для повного переліку впливових змінних.

 

 

 

 

 

 

 

 

 

 

Таблиця 8.6

 

 

План ДФЕ

для повного переліку змінних

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

№ досліду

 

 

 

 

Список суттєвих факторів

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

+1

 

–1

 

–1

+1

+1

–1

–1

 

+1

2

+1

 

+1

 

–1

–1

–1

–1

+1

 

+1

384

Розділ 8

3

+1

–1

+1

–1

–1

+1

–1

+1

4

+1

+1

+1

+1

+1

+1

+1

+1

 

 

 

 

 

 

 

 

 

Отримана матриця має співпадаючі стовпці: і ; і ; і , і . Практично неможливо розділити дію змінних, які змінюються однаково.

Саме тому, якщо зробити спробу оцінити коефіцієнти регресії , , , , то кожна із оцінок цих коефіцієнтів буде враховувати дію відразу деяких змінних: оцінка

– дію не тільки фактора , але і взаємодії , яка змінюється в експерименті аналогічним чином; оцінка – спільну дію фактора і змінної ; оцінка – не тільки вільного члена , але і результат впливу змінної . Інакше кажучи, – спільна оцінка для коефіцієнтів і ; – для і , – для і , – для і . Звідки виходить, що за допомогою ДФЕ при даному списку суттєвих змінних відшукати необхідне рівняння регресії неможливо і слід використати ПФЕ .

Приклад 2. Нехай заданий список суттєвих змінних: , , , , , , . Перевіримо можливість використання плану ДФЕ .Маємо . Оскільки , необхідну умову (8.14) виконано і можна зробити спробу побудувати план ДФЕ 24-1.

Для складання матриці плану виберемо фактори , , . Для фактора необхідно зазначити генеруюче співвідношення. Розглянемо два варіанти і (табл. 8.7).

 

 

 

 

 

 

 

 

 

Таблиця 8.7

 

 

 

План ДФЕ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

№ досліду

 

 

Список суттєвих факторів

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Перший варіант (

 

 

)

 

 

1

+1

–1

–1

 

–1

–1

 

+1

+1

 

2

+1

+1

–1

 

–1

+1

 

–1

+1

 

3

+1

–1

+1

 

–1

+1

 

–1

–1

4

+1

+1

+1

 

–1

–1

 

+1

–1

5

+1

–1

–1

 

+1

+1

 

+1

–1

6

+1

+1

–1

 

+1

–1

 

–1

–1

7

+1

–1

+1

 

+1

–1

 

–1

+1

 

8

+1

+1

+1

 

+1

+1

 

+1

+1

 

 

 

Другий варіант (

 

)

 

 

 

1

+1

–1

–1

 

–1

+1

 

+1

+1

 

2

+1

+1

–1

 

–1

+1

 

–1

+1

 

3

+1

–1

+1

 

–1

–1

 

–1

–1

4

+1

+1

+1

 

–1

–1

 

+1

–1

5

+1

–1

–1

 

+1

–1

 

+1

–1

Дослідження систем методом планування експериментів

385

6

+1

+1

–1

+1

–1

–1

–1

 

7

+1

–1

+1

+1

+1

–1

+1

 

8

+1

+1

+1

+1

+1

+1

+1

 

У першому варіанті серед стовпців немає співпадаючих або повністю протилежних. Тому цей план може бути використаний при експериментуванні. До такого ви-

сновку прийдемо, якщо застосуємо генеруючи співвідношення

.

У другому варіанті співпадають два стовпця та

, тобто всі змінні із списку

суттєвих будуть змінюватися в експерименті однаково, що неприпустимо.

 

Розглянуті приклади показують, що ефективність застосування ДФЕ залежить від вдалого вибору системи змінювання лінійних ефектів з ефектами взаємодії. Щоб визначити заздалегідь, в яких стовпцях однакові елементи, використовують визначальні контрасти

(ВК).

Визначальний контраст – це співвідношення між змінними, яке у всіх дослідах задає елементи першого фіктивного стовпця () матриці планування.

У кожному плані ДФЕ кількість визначальних контрастів дорівнює кількості генеруючих співвідношень. Для створення визначального контрасту достатньо помножити генеруюче співвідношення зліва і справа на нововведений фактор із змішаною оцінкою та використати

умову .

В прикладі 1 для першого варіанта змішану оцінку має фактор . Помноживши обидві частини цього співвідношення на , отримаємо

 

.

Звідси маємо визначальний контраст

.

Помноживши по черзі визначальний контраст на відповідні факто-

ри, отримаємо систему змінювання спільних оцінок для коефіцієн-

тів рівняння регресії:

 

;

;

;

;

;

;

386

Розділ 8

Для другого варіанту за допомогою генеруючого співвідношення утворимо визначальний контраст

.

Система змішування оцінок буде такою:

;

;

;

;

;

.

Дробові репліки факторних планів характеризуються розв’язува-

льною здатністю, порядок якої залежить від кількості факторів у

визначальному контрасті. Розв’язувальна здатність тим вища, чим вищий порядок взаємодій, з оцінками коефіцієнтів яких змішані оцінки головних ефектів. Розв’язувальна здатність півреплік у розглянутих варіантах однакова і дорівнює трьом.

Для чотирифакторних планів маємо вісім можливостей створення півреплік . Розглянемо дві з них, що задані генеруючими співвідношеннями і .

Для першого генеруючого співвідношення визначальний контраст

.

За його допомогою знаходимо систему змішування оцінок коефіцієнтів регресії:

;

;

; ;

; ; ; .

Визначальний контраст другого генеруючого співвідношення має вигляд:

.

Система змішування оцінок:

Дослідження систем методом планування експериментів

387

; ;

; ;

; ;

; ;

; ;

; ;

; ;

З погляду аналізу проблеми змішування оцінок розглянуті піврепліки не еквівалентні. У другій піврепліці оцінки лінійних коефіцієнтів змішані з оцінками потрійних взаємодій, які в реальних задачах дорівнюють нулю частіше, ніж подвійні. Тому друга піврепліка має більшу розв’язувальну здатність порівняно з першою.

Репліки, що мають максимальну розв’язувальну здатність, нази-

ваються головними.

Експериментатор, який не має апріорної інформації щодо ефектів взаємодії, повинен намагатися вибрати дробову репліку з найбільшою розв’язувальною здатністю.

Для реплік вищої дробовості порядок визначення системи змішуваних оцінок такий самий, як для півреплік. В ДФЕ з такими репліками кількість генеруючих співвідношень визначається ступенем дробовості (табл. 8.8).

 

 

 

 

Таблиця 8.8

 

 

Репліки вищої дробовості

 

 

 

 

 

Кількість

Тип

 

Ступінь

Кількість генеруючих

 

факторів

ДФЕ

 

дроблення

співвідношень

 

 

 

 

 

5

25–2

 

1/4

2

 

6

26–3

 

1/8

3

 

7

27–4

 

1/16

4

 

При побудові дробової репліки використовують узагальнений визначальний контраст (УВК), який визначається як добуток частинних контрастів. Наприклад, 1/4 репліка у одному із варіа-

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности