
big_doc_LKG
.pdf
|
|
Дослідження систем методом планування експериментів |
369 |
||||
економічне тлумачення, бути однозначною функцією факторів і |
|||||||
легко вимірюватись та приводити до поставленої мети. Функ- |
|||||||
цію відгуку при оптимізації систем іноді називають цільовою, а факто- |
|||||||
ри |
, |
, , |
– керованими параметрами. |
|
|
||
|
z2 |
|
|
z2 |
|
|
|
|
|
|
80 |
|
70 |
|
|
|
|
|
90 |
|
|
|
|
|
|
|
100 |
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
z1 |
|
|
|
z1 |
|
|
|
а) |
|
|
б) |
|
|
z2 |
|
|
z2 |
|
|
|
|
|
|
80 |
|
|
50 |
|
|
|
|
90 |
70 |
|
60 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
100 |
|
50 |
60 |
|
|
|
|
|
|
70 |
|
|
|
|
|
90 |
40 |
|
|
|
|
|
|
|
|
|
||
|
|
|
80 |
|
|
|
|
|
|
|
z1 |
|
|
|
z1 |
|
|
|
в) |
|
|
г) |
|
|
|
|
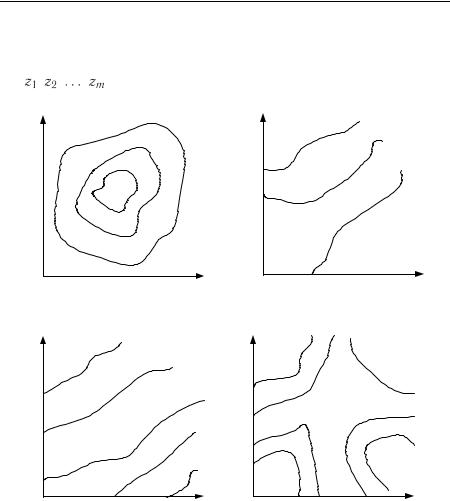
Рис. 8.1. Види поверхонь відгуків: |
|
|
||
|
|
параболоїд (а), стаціонарне підвищення (б), |
хребет (в), сідло (г) |
|
|||
|
Математичним апаратом теорії планування експерименту є теорія |
||||||
імовірності, математична статистика, математичне програ- |
|||||||
мування і чисельні методи. |
|
|
|
|
|||
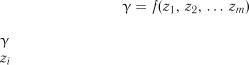
Дослідження систем методом планування експериментів |
371 |
(рандомізувати) змінні, що діють систематично, або такі, які не можна урахувати і проконтролювати. У цьому разі досліджувані змінні можна розглядати як випадкові величини і, отже, враховувати статистично. При практичній реалізації процедури рандомізації обов’язково повинен використовуватися механізм типу «лотереї» або таблиць рівно-
мірно розподілених випадкових чисел.
5. Принцип оптимальності планування експерименту. Цей принцип є центральним в теорії планування експериментів. У відповідності з ним план експерименту повинен мати деякі оптимальні властивості з точки зору певного, заздалегідь вибраного критерію оптимальності плану або сукупності таких критеріїв.
8.3. Загальна схема дослідження систем методом планування експерименту
Сутність планування експерименту полягає у тому, що при проведенні досліджень експеримент, керований з використанням математичних методів за деяким певним планом, проводиться в декілька послідовних етапів. При цьому після кожного етапу розглядається питання про зміну стратегії експерименту.
У виробничих системах часто виникає така задача. Виявлено  змінних (факторів)
змінних (факторів)  (
( ), від яких залежить результативний показник процесу функціонування системи
), від яких залежить результативний показник процесу функціонування системи  . Самі змінні можуть і не бути випадковими, так як їх значення можуть бути заданими. Однак на величину
. Самі змінні можуть і не бути випадковими, так як їх значення можуть бути заданими. Однак на величину  впливають і інші, які не піддаються точному контролю змінні. Тому величина
впливають і інші, які не піддаються точному контролю змінні. Тому величина  носить випадковий характер. Для цих умов необхідні методи експериментального визначення впливу змінних на величину показника
носить випадковий характер. Для цих умов необхідні методи експериментального визначення впливу змінних на величину показника  .
.
Математично задача формулюється таким чином: необхідно отри-
мати уяву щодо функції відгуку |
|
|
|
, |
(8.1) |
де |
– характеристика досліджуваного процесу; |
|
|
– незалежні змінні, які можна змінювати при постановці |
|
|
експерименту. |
|
Дослідження систем методом планування експериментів |
373 |
Етап 1. Підготовка до експерименту. На цьому етапі розв’язують такі задачі.
1. Вибір критерію оцінки досліджуваного процесу. Критерій ефективності бажано мати такий, щоб він однозначно і достатньо повно характеризував ефективність об’єкту дослідження. Слід прагнути до того, щоб критерій був тільки одним, таким, що може оцінюватися кількісно з максимальною статистичною ефективністю і має природний фізичний сенс. Не рекомендується вибирати в якості критерію ефективності показники, які не можна виміряти, наприклад, виражені в процентах, в логарифмічних і тригонометричних функціях тощо.
Критерій (або параметр) ефективності – це реакція (відгук) на дію факторів, які визначають поведінку досліджуваної системи. Такі пара-
метри можуть бути економічними, виробничо-технічними, статистичними, психологічними, тактико-технічними тощо.
Параметри ефективності повинні задовольняти таким вимогам:
–бути кількісними і задаватися одним числом;
–допускати вимірювання за будь-якою можливою комбінацією вибраних рівнів факторів;
–бути універсальними, тобто всебічно характеризувати об’єкт дослідження;
–мати простий вигляд;
–існувати на всіх стадіях проведення експерименту.
2. Вибір незалежних змінних (факторів). Після вибору критеріїв оцінки вибирають керовані фактори – змінні, дію яких на об’єкт дослідження можна змінювати цілеспрямовано. До розгляду необхідно включити всі існуючі фактори, які можуть спричиняти дії на досліджуваний об’єкт. Кількість вибраних факторів обумовлює розмірність досліджуваного факторного простору. Фактори визначають сам об’єкт дослідження або його стан. Можна сформулювати такі вимоги до факторів.
Незалежність, тобто можливість встановлення фактора на будьякому рівні без залежності від рівнів інших факторів.
Сумісність полягає у тому, що всі їх комбінації можна здійснити. Керованість означає, що планувати експеримент можна у тому
випадку, якщо рівні факторів підкорюються волі експериментатора. Точність вимірювання. Ступінь точності визначається діапазоном
змінювання факторів.
Однозначність, тобто безпосередня дія факторів на об’єкт.

Дослідження систем методом планування експериментів |
375 |
 . (8.7)
. (8.7)
Ця модель за допомогою критерію Фішера перевіряється на адекватність, тобто відповідність експериментальним точкам.
Якщо лінійна модель неадекватна, то поліном добудовують до неповної квадратичної моделі, в якій враховуються ефекти взаємодії або їх комбінації
. (8.8)
Після цього знову перевіряють адекватність неповної квадратичної моделі. За необхідності, цю модель добудовують до повної квад-
ратичної моделі
(8.9)
Етап 2. Планування експерименту. Якщо вибрана модель плану-
вання, тобто вигляд функції  , і записано її рівняння, то залишається у відведеній для дослідження області факторного простору
, і записано її рівняння, то залишається у відведеній для дослідження області факторного простору  спланувати експеримент для оцінки числових значень констант (коефіцієнтів) цього рівняння.
спланувати експеримент для оцінки числових значень констант (коефіцієнтів) цього рівняння.
Так як поліноми (8.7) – (8.9) містять  коефіцієнтів, які підля-
коефіцієнтів, які підля-
гають визначенню, то план експерименту Р повинен містити принаймні  різних експериментальних точок
різних експериментальних точок
|
|
|
, |
(8.10) |
де |
– значення, яке приймає і-та змінна в j-му випробовуванні |
|||
|
( |
, |
). |
|
Після реалізації в |
|
точках області факторного простору, відведе- |
||
ної для експериментування, отримаємо вектор спостережень у вигляді

Дослідження систем методом планування експериментів |
377 |
Етап 4. Реалізація планів експерименту. Вибирають спосіб прове-
дення експерименту (натурний чи машинний), встановлюють порядок проведення експерименту і отримують числові значення функції відгуку.
Етап 5. Статистичний аналіз результатів експерименту. Викону-
ється перевірка точності оцінок параметрів отриманої регресійної моделі і її відповідність даним експерименту.
8.4. Дослідження систем за допомогою планів першого порядку
8.4.1. Складання планів експерименту. Плани першого порядку призначені для експериментального отримання лінійних регресійних моделей (8.7)–(8.8). В цих моделях для визначення функції відгуку  використовуються плани експерименту з варіюванням всіх
використовуються плани експерименту з варіюванням всіх  факторів на двох рівнях. Такі плани називаються планами типу
факторів на двох рівнях. Такі плани називаються планами типу  . Кількість всіх можливих дослідів дорівнює
. Кількість всіх можливих дослідів дорівнює  .
.
В дослідницькій практиці найбільш поширеними є два різновиди планів першого порядку:
–повний факторний експеримент (ПФЕ);
–дробовий факторний експеримент (ДФЕ).
|
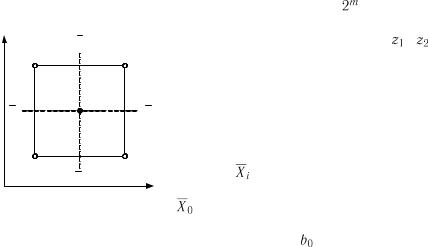
8.4.1.1. Повний факторний експеримент. В експерименті при |
||||||
дворівневій системі вимірювань факторів реалізуються всі можливі |
|||||||
сполучення факторів. Такий план позначається як ПФЕ . |
|
|
|||||
z2 |
|
|
Для найпростішої лінійної моделі, яка |
||||
X 2 |
|
включає два незалежних фактори |
i |
, |
|||
|
|
||||||
|
( 1; 1) |
( 1; 1) |
план ПФЕ геометрично можна предста- |
||||
|
2 |
3 |
вити у вигляді площини з чотирма (за кі- |
||||
|
0 |
|
лькістю дослідів) вершинами (рис. 8.2). |
|
|||
|
X1 |
План факторного експерименту зру- |
|||||
|
X 20 |
чно представити у вигляді матриці пла- |
|||||
|
|
|
|||||
|
1 |
4 |
нування, яка включає: |
|
|
||
|
– кодовані значення рівнів кожного |
||||||
|
( 1; 1) |
( 1; 1) |
|||||
|
фактора |
; |
|
|
|
||
|
X10 |
|
|
|
|
||
|
|
– стовпець з |
фіктивним фактором |
||||
|
|
z1 |
|||||
|
|
, що набуває одного значення у всіх |
|||||
|
|
|
|||||
|
Рис. 8.2. Геометрична |
дослідах, за допомогою якого визнача- |
|||||
|
інтерпретація ПФЕ типу 22 |
ється вільний член |
функції відгуку; |
|
|||

 ,
,  , ,
, ,  – змінні величини, які можуть набувати при проведенні експерименту задане значення і визначатися кількісно.
– змінні величини, які можуть набувати при проведенні експерименту задане значення і визначатися кількісно. , що являє собою
, що являє собою  при експериментуванні.
при експериментуванні. , в якій знаходяться точки, що відповідають умовам проведення дослідів використовуваного плану експерименту. Якщо область планування задається
, в якій знаходяться точки, що відповідають умовам проведення дослідів використовуваного плану експерименту. Якщо область планування задається  (
( ), то вона являє собою
), то вона являє собою  , (8.2)
, (8.2) – значення функції відгуку в початку координат;
– значення функції відгуку в початку координат; ;
; ,
,  ,
,  ,
,  є статистичними оцінками невідомих теоретичних коефіцієнтів
є статистичними оцінками невідомих теоретичних коефіцієнтів  ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  в рівнянні (8.2)
в рівнянні (8.2) ;
; ;
; , де
, де  , обмеженій значенням факторів
, обмеженій значенням факторів  .
. від
від  змінних, який містить
змінних, який містить  коефі-
коефі- – реакція, яка відповідає
– реакція, яка відповідає 
 ).
). , отримаємо матрицю планування розмірністю
, отримаємо матрицю планування розмірністю 
 (
( ) на декількох рівнях відносно початкової точки
) на декількох рівнях відносно початкової точки  , яка представляє собою
, яка представляє собою 
