
big_doc_LKG
.pdf

Апроксимація зв’язків багатофакторними регресійними моделями 359
статистику
 .
.
Із табл. 1.13 для  і
і  визначаємо критичні межі критерію
визначаємо критичні межі критерію  і
і  . Так як
. Так як  , то робимо висновок,
, то робимо висновок,
що результативна ознака  відповідає нормальному закону розподілу. Для другої вибірки (пункт 2) маємо:
відповідає нормальному закону розподілу. Для другої вибірки (пункт 2) маємо:
 ;
;  ;
;  ;
;
.
Отже, друга вибірка відповідає нормальному розподілу. Для третьої вибірки (пункт 3) маємо:
 ;
;  ;
;  ;
;
.
Отже, третя вибірка відповідає нормальному закону розподілу.
Виявлення наявності аномальних спостережень. Для виконання цієї операції статистичні дані всіх ознак розташовуємо у порядку зростання значень. Розглянемо першу упорядковану вибірку (табл. 7.5).
Таблиця 7.5
Результати виявлення викидів у першій вибірці
№ |
Упорядковані значення ознак |
№ |
Упорядковані значення ознак |
||||||||||
п/п |
|
|
|
|
|
|
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
120 |
5 |
0,12 |
0,31 |
2,0 |
0,34 |
10 |
497 |
14 |
0,35 |
0,79 |
4,5 |
0,96 |
2 |
126 |
5 |
0,12 |
0,42 |
2,3 |
0,34 |
11 |
564 |
15 |
0,37 |
0,79 |
4,5 |
1,00 |
3 |
157 |
5 |
0,15 |
0,43 |
2,4 |
0,34 |
12 |
651 |
16 |
0,40 |
0,79 |
5,0 |
1,10 |
4 |
240 |
6 |
0,19 |
0,52 |
2,7 |
0,41 |
13 |
671 |
17 |
0,45 |
0,79 |
5,3 |
1,16 |
5 |
367 |
6 |
0,21 |
0,55 |
3,0 |
0,41 |
14 |
714 |
19 |
0,48 |
0,81 |
5,3 |
1,30 |
6 |
396 |
10 |
0,21 |
0,60 |
3,6 |
0,68 |
15 |
742 |
20 |
0,57 |
0,88 |
5,7 |
1,37 |
7 |
429 |
13 |
0,21 |
0,63 |
4,0 |
0,89 |
16 |
815 |
22 |
0,58 |
1,00 |
6,0 |
1,50 |
8 |
482 |
14 |
0,21 |
0,65 |
4,3 |
0,96 |
17 |
1119 |
39* |
0,69 |
1,00 |
13,0* |
2,67* |
9 |
494 |
14 |
0,30 |
0,70 |
4,3 |
0,96 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|




|
Апроксимація зв’язків багатофакторними регресійними моделями |
363 |
|||||||||
|
|
|
|
|
|
|
|
|
Таблиця 7.9 |
||
|
|
Матриці коефіцієнтів кореляції |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Форма |
|
|
|
|
|
|
Результати |
|||
|
представлення |
|
Кореляційні матриці |
|
|||||||
|
|
|
|
аналізу |
|||||||
|
вихідних даних |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1. Первинна |
Ознаки |
|
|
|
|
|
Несуттєвий |
|
||
|
вибірка |
|
|
|
|
|
фактор . |
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
0,323 |
0,615 |
–0,867 |
–0,900 |
–0,004 |
|
|
|||
|
|
|
Мультиколіне- |
||||||||
|
|
|
|
|
|
|
|
арні фактори |
|||
|
|
|
1 |
–0,002 |
–0,027 |
0,077 |
–0,930 |
||||
|
|
|
і |
; |
і . |
||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
0,977 |
0,137 |
0,065 |
Виключаємо |
|||
|
|
|
|
, . |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
0,171 |
0,071 |
|
|
||
|
|
|
|
|
Концептуальна |
||||||
|
|
|
|
|
|
|
|
модель |
|
|
|
|
|
|
|
|
|
1 |
0,059 |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2. Викиди |
Ознаки |
|
|
|
|
|
Несуттєві |
фак- |
|
|
|
замінено |
|
|
|
|
|
тори |
, . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
середніми |
|
0,688 |
–0,080 |
0,127 |
0,023 |
–0,110 |
Мультиколіне- |
|||
|
значеннями |
|
|
|
|
|
|
арні фактори |
|||
|
|
1 |
0,016 |
–0,092 |
0,038 |
–0,871 |
|||||
|
ознак |
|
і |
; |
і . |
||||||
|
|
|
|
|
|
|
|
Виключаємо |
|||
|
|
|
|
1 |
0,905 |
0,034 |
0,044 |
||||
|
|
|
|
, |
, . |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
0,097 |
0,065 |
Концептуальна |
|||
|
|
|
|
|
|
|
|
модель |
|
|
|
|
|
|
|
|
|
1 |
0,047 |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
3. Із вибірок |
Ознаки |
|
|
|
|
|
Несуттєвий |
|
||
|
виключені всі |
|
|
|
|
|
фактор . |
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
спостереження з |
|
0,466 |
0,707 |
0,516 |
–0,170 |
–0,020 |
Мультиколіне- |
|||
|
викидами |
|
|
|
|
|
|
арні фактори |
|||
|
|
1 |
0,233 |
0,244 |
0,190 |
–0,796 |
|||||
|
|
|
і . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
0,978 |
0,181 |
–0,006 |
Виключаємо |
|||
|
|
|
|
, . |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
0,161 |
–0,090 |
|
|
||
|
|
|
|
|
Концептуальна |
||||||
|
|
|
|
|
|
|
|
модель |
|
|
|
|
|
|
|
|
|
1 |
–0,001 |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
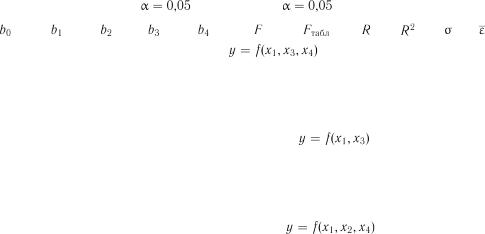
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблиця 7.10 |
||
|
|
|
Результати розрахунку регресійних моделей |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Значення та значимість |
|
Адекватність |
|
Оцінки якості |
|
|||||||
|
Модель |
коефіцієнтів регресії ( |
|
) |
моделі ( |
) |
регресійної моделі |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, % |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Первинна вибірка, модель |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. Лінійна |
206,7 |
9,480 |
– |
|
304,6 |
–10,77 |
5,54 |
|
8,53 |
0,516 |
0,266 |
188,7 |
|
28,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Степенева |
228,83 |
0,3797 |
– |
|
0,405 |
–0,081 |
7,50 |
|
8,53 |
0,573 |
0,329 |
188,1 |
|
29,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Показникова |
220,28 |
1,013 |
– |
|
2,750 |
0,962 |
6,17 |
|
8,53 |
0,538 |
0,187 |
196,4 |
|
31,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Викиди замінено середніми значеннями, модель |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. Лінійна |
4,78 |
24,37 |
– |
|
253,9 |
– |
22,52 |
|
19,5 |
0,699 |
0,489 |
157,4 |
|
24,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Степенева |
156,49 |
0,528 |
– |
|
0,677 |
– |
25,86 |
|
19,5 |
0,724 |
0,524 |
165,1 |
|
26,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Показникова |
111,5 |
1,049 |
– |
|
2,920 |
– |
25,03 |
|
19,5 |
0,718 |
0,516 |
167,5 |
|
26,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Виключені спостереження з викидами, модель |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Лінійна |
434,40 |
6,790 |
103,16 |
|
– |
–12,37 |
3,28 |
|
8,53 |
0,510 |
0,260 |
84,08 |
|
13,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Степенева |
407,89 |
0,172 |
0,042 |
|
– |
–0,133 |
2,75 |
|
8,53 |
0,477 |
0,227 |
85,41 |
|
13,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Показникова |
437,03 |
1,013 |
1,209 |
|
– |
0,974 |
3,07 |
|
8,53 |
0,497 |
0,247 |
84,66 |
|
13,38 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примітка: напівжирним шрифтом позначені значимі результати

Апроксимація зв’язків багатофакторними регресійними моделями 365
Питання для самоперевірки
1.Охарактеризуйте основні рекомендації щодо відбору факторів для включення їх у регресійну модель.
2.Назвіть типи парних коефіцієнтів кореляції у множинному регресійному аналізі.
3.Як визначається наявність мультиколінеарності між факторами?
4.Як визначається мінімальна кількість спостережень для побудови багатофакторної регресійної моделі?
5.Назвіть основні типи залежностей у багатофакторних моделях.
6.Викладіть процедуру побудови лінійної багатофакторної регресійної моделі.
7.Як визначається коефіцієнт множинної кореляції?
8.Як обчислюють стандартизовані коефіцієнти регресії?
9.Назвіть методи перевірки значимості коефіцієнта множинної кореляції.
10.Що представляє собою множинний коефіцієнт детермінації?
11.У чому полягає сутність апроксимації методом покрокового включення факторів у модель?
12.У чому полягає сутність апроксимації методом покрокового виключення факторів з моделі?
13.У чому полягає сутність апроксимації методом добутку функцій?
14.За яким показником приймають рішення про включення фактора до моделі?
15.За яким критерієм приймають рішення про виключення фактору з моделі?
16.Поясніть порядок розрахунку степеневих та показникових регресійних моделей.
Література
1.Воевудский, Е. Н. Экономико-математические модели и методы в управлении морским транспортом: Учебник для студентов морских вузов [Текст] / Е. Н. Воевудский, Н. А. Коневцева, Г. С. Махуренко, И. П. Тарасова.– М.: Транспорт, 1988.– 384 с.
2.Дрейпер, Н. Прикладной регрессионный анализ [Текст]: в 2 кн. / Н. Дрейпер, Г. Смит.– М.: Финансы и статистика, 1986.– 366 с.
3.Львовский, Е. Н. Статистический методы построения эмпирических формул: учебное пособие [Текст] / Е. Н. Львовский.– М.: Высшая школа, 1982.– 224 с.
РОЗДІЛ 8
ДОСЛІДЖЕННЯ ТРАНСПОРТНИХ ПРОЦЕСІВ І СИСТЕМ МЕТОДОМ ПЛАНУВАННЯ ЕКСПЕРИМЕНТІВ
Мета вивчення теми – оволодіти методами дослідження і аналізу процесів функціонування транспортних систем на основі багатофакторного активного експерименту.
Після вивчення теми ви повинні вміти:
–представляти систему або процес у вигляді математичної моделі;
–виділяти характерні групи факторів, які впливають на функціонування об’єкта;
–вибирати і обґрунтовувати критерії ефективності досліджуваного процесу, незалежні змінні (фактори) і види апроксимуючих поліномів;
–складати математичні моделі різної складності для процесів функціонування транспортних процесів;
–складати математичні плани експериментів для різних за складністю і видом функціональних залежностей вихідної характериcтики досліджуваного процесу від факторів;
–розробляти, організовувати і проводити факторні експерименти при дослідженні систем;
–визначати і оцінювати параметри регресійних залежностей за даними активного експерименту;
–відшукувати оптимальні режими функціонування багатофакторних об’єктів.
8.1. Основні поняття теорії планування експериментів
Теорія планування експерименту призначена для розв’язування типових задач дослідження (типові прийоми для типових задач). До основних найбільш розповсюджених типових задач дослідження відносять:
1) отримання деяких попередніх відомостей про процес (опрацювання літературних даних, опитування спеціалістів і аналіз результатів опитування, експеримент);
Дослідження систем методом планування експериментів |
367 |
2)отримання формальних залежностей;
3)перевірку гіпотез, тобто деяких змістовних припущень про властивості об’єкта;
4)оптимізацію властивостей досліджуваного об’єкта.
Під плануванням експерименту розуміють всю сукупність дій, які спрямовані на розробку стратегії експериментування від початкових до заключних станів об’єкта дослідження, тобто від одержання апріорної інформації до створення дієздатної математичної моделі або визначення оптимальних умов.
В основу планування експерименту покладений активний експеримент, тобто коли існують тільки фактори деякої групи і експериментатор у відповідності з планом експерименту може цілеспрямовано їх оцінювати.
Активний експеримент передбачає можливість активно діяти на досліджуваний об’єкт. При використанні методів активного експерименту математичний опис будується у вигляді сукупності статичних і динамічних вихідних характеристик об’єкта, які реєструються при подаванні на його входи спеціальних збурювальних дій. При активному експерименті можна строго перевірити адекватність моделі і вжити необхідних заходів для виконання умов, необхідних для застосування методу множинного регресійного аналізу, який використовується для опрацювання результатів експерименту.
Активний експеримент проводиться за заздалегідь складеним планом. У відповідності з цим планом експериментатор діє на вхідні параметри досліджуваного об’єкта, а вихідні параметри, відбиваючи реакцію досліджуваного об’єкта на керівні дії, дають змогу з’ясувати природу процесів, що відбуваються в об’єкті дослідження.
Планування експерименту при аналізі процесу функціонування систем і встановленні взаємозв’язків між змінними полягає у виборі кількості та умов проведення дослідів, за яких можна дістати потрібні результати із заданою точністю. Схема експериментів нагадує схему кібернетичної «чорної скриньки», властивості якої встановлюються аналізом залежності вимірюваних ендогенних (залежних) величин при певних комбінаціях рівнів контрольованих екзогенних (неза-
лежних) величин. В результаті експерименту отримують рівняння регресії (модель процесу). Розглянемо визначення основних категорій теорії планування експериментів.

 , стандартного відхилення емпіричного розподілу
, стандартного відхилення емпіричного розподілу  , стандартне відхилення незміщеної оцінки для дисперсії теоретичного розподілу
, стандартне відхилення незміщеної оцінки для дисперсії теоретичного розподілу  , коефіцієнта варіації
, коефіцієнта варіації  ) наведені у табл. 7.4.
) наведені у табл. 7.4. – незміщене стандартне відхилення.
– незміщене стандартне відхилення. розмаху варіювання (1.3.1).
розмаху варіювання (1.3.1). обчислюємо величину розмаху
обчислюємо величину розмаху ;
;
 ;
;  . Обчислюємо статистики відповідно для найбільшого
. Обчислюємо статистики відповідно для найбільшого  та найменшого
та найменшого  значень даних спостережень
значень даних спостережень ;
;  .
. і
і  знаходимо критичні значення
знаходимо критичні значення ,
,  .
. та
та  , то гіпотеза про наявність викидів у вибірці
, то гіпотеза про наявність викидів у вибірці 
 ,
,  . Обчислюємо статистики критерію Груббса:
. Обчислюємо статистики критерію Груббса: і
і  критичні значення критерію
критичні значення критерію  ;
;  . Так як
. Так як  і
і  , то гіпотеза про наявність викидів у вибірці
, то гіпотеза про наявність викидів у вибірці  , мінімальна кількість спостережень повинна складати
, мінімальна кількість спостережень повинна складати .
. . Результати перевірки (розрахунки виконані за формулою (1.57) наведені у табл. 7.8.
. Результати перевірки (розрахунки виконані за формулою (1.57) наведені у табл. 7.8. ) і задовольняє умові адекватності (
) і задовольняє умові адекватності ( ). Ця модель описується залежністю
). Ця модель описується залежністю .
.