big_doc_LKG

Апроксимація зв’язків багатофакторними регресійними моделями 349

До початкового списку з чотирьох змінних система додала чотири їх перетворення. Тобто, наприклад, значення змінної LN–V1 є значеннями логарифмів змінної Х1. Зауважимо, що у лівому списку залежних змінних можна вибирати декілька змінних. При побудові степеневої та показникової моделей необхідно вибирати замість залежної змінної Y її логарифмічне перетворення (у нашому випадку LN–V4).

Устепеневій залежності замість незалежних змінних Х1, Х2,…, Хn слід вказати їх логарифмічні перетворення (у нашому випадку відпові-

дно LN–V1, LN–V2, LN–V3).

Упоказниковій залежності незалежні змінні у відповідності до рівняння (7.43) використовуються без перетворення, тобто у правому списку незалежних змінних слід вибрати їх дійсні значення (у нашому прикладі Х1, Х2 та Х3);

5) після вибору залежної та незалежних змінних у діалоговому вікні MODEL DEFINITION – ВИЗНАЧЕННЯ МОДЕЛІ (рис. 7.7) слід вказати, чи необхідно включити до моделі вільний член у списку натиснути кнопку INTERCEPT – ВІЛЬНИЙ ЧЛЕН (рис. 7.8) та натиснути кнопку ОК;

6) викликавши вікно з електронною таблицею результатів розрахунку коефіцієнтів регресії аналогічно вищеописаному для лінійної моделі перейти від перетворених коефіцієнтів регресії до дійсних. Розглянемо порядок визначення дійсних коефіцієнтів регресії за степеневою та показниковою моделями для нашого прикладу.

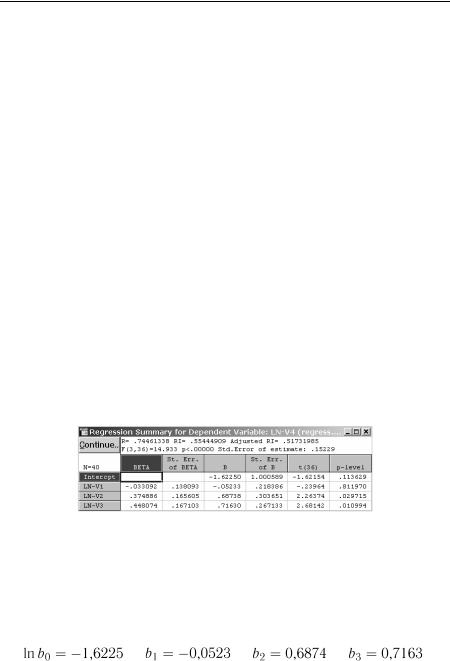
Вікно результатів розрахунку коефіцієнтів регресії для степеневої моделі показане на рис. 7.13.

Рис. 7.13. Результати розрахунків коефіцієнтів регресії за степеневою моделлю

Таким чином, коефіцієнти при перетворених змінних у лінійованому рівнянні степеневої регресії (7.28) мають наступні значення (стовпчик В таблиці результатів на рис. 7.13):

Апроксимація зв’язків багатофакторними регресійними моделями 351

7.4.3. Оцінка якості регресійних залежностей. Якість побудова-

них рівнянь регресії можна оцінити за допомогою розрахункових показників, до яких відносяться:

–коефіцієнт множинної кореляції (позначається як MULTIPLE R чи просто R);

–коефіцієнт множинної детермінації (позначається як R2 чи RI);

–стандартна помилка оцінювання регресії (позначається як STAN-

DARD ERROR OF ESTIMATE чи STD. ERROR OF ESTIMATE).

Результати розрахунку цих показників виводяться в процесі побудови регресійної моделі у верхній частині діалогового вікна MULTIPLE

REGRESSION RESULTS – РЕЗУЛЬТАТИ МНОЖИННОЇ РЕГРЕСІЇ (рис. 7.5)

та дублюються у верхній частині вікна результатів розрахунків коефіцієнтів регресії (рис. 7.6).

Регресійна модель буде кращою серед декількох розглянутих, якщо їй відповідають більші значення коефіцієнтів множинної кореляції та множинної детермінації та менші значення стандартної помилки оцінювання регресії.

7.4.3.1. Оцінка значимості рівняння та факторів регресії. Для перевірки значимості рівняння регресії та адекватності рівняння регресії вихідним даним використовується -критерій Фішера (F). Розрахунковий критерій Фішера виводиться у правому стовпчику верхньої частині діалогового вікна MULTIPLE REGRESSION RESULTS – РЕ-

ЗУЛЬТАТИ МНОЖИННОЇ РЕГРЕСІЇ (рис. 7.5) та для нашого прикладу дорівнює .

Нижче значення F виводиться кількість ступенів вільності меншої дисперсії та кількість ступенів волі більшої дисперсії (рядок DF). У нашому прикладі відповідно 3 та 36.

Ще нижче виводиться гранична імовірність прийняття гіпотези про адекватність регресійної моделі вихідним даним (у нашому прикладі p=0,000004).

У випадку, коли розрахункове значення граничної імовірності прийняття гіпотези про адекватність регресійної моделі вихідним даним не перевищує вибраний рівень значимості регресійна модель вважається значимою та адекватною вихідним експериментальним (статистичним) даним.

Для розглянутого прикладу при рівні значимості 0,05 лінійну множинну регресійну модель можна вважати значимою та адекватною ви-

хідним даним, так як p=0,000004 < 0,05.

Апроксимація зв’язків багатофакторними регресійними моделями 355

7.4.3.3. Розрахунок кореляційної матриці. Розрахунок кореляцій-

ної матриці дає можливість виявити, так звані, мультиколінеарні фактори, тобто пари факторів, між якими існує значимий кореляційний зв’язок (один фактор залежить від другого чи навпаки). Кореляційна матриця є квадратною та містить стільки рядків та стовпчиків, скільки незалежних змінних міститься у рівнянні регресії.

Для побудови кореляційної матриці слід натиснути у вікні MULTIPLE REGRESSION RESULTS – РЕЗУЛЬТАТИ МНОЖИННОЇ РЕГРЕСІЇ (рис.

9.5) кнопку – КОРЕЛЯЦІЙНІ ТА ОПИСОВІ СТАТИС-

ТИКИ, після чого на екрані з’явиться діалогове вікно REVIEW DESCRIPTIVE STATISTIC – ПЕРЕГЛЯД ОПИСОВИХ СТАТИСТИК (рис. 7.20).

Рис. 7.20. Діалогове вікно описових статистик

Надалі у цьому вікні слід натиснути кнопку – КОРЕЛЯЦІЯ. Вікно результатів розрахунку кореляційної матриці для вихідних даних нашого прикладу наведене на рис. 7.21.

Рис. 7.21. Кореляційна матриця

Значимі коефіцієнти кореляції підсвічуються червоним кольором на рівні значимості 0,05.

Апроксимація зв’язків багатофакторними регресійними моделями 357

Приклад 2. Проведені дослідження на трьох однотипних вантажних пунктах металургійного комбінату дали підстави стверджувати, що величина загального прос-

тою вагонів на комбінаті залежить від таких, апріорі вибраних, факторів:

– сумарної кількості вагонів, що надходять в систему за добу;

– частки вантажів, що надходять в критих вагонах;

– частки вантажів, що надходять в піввагонах;

– інтервалів між черговим прибуттям вагонів;

– коефіцієнта завантаження транспортної системи.

В табл. 7.3 наведені статистичні дані спостережень, зібрані на трьох однотипних вантажних пунктах.

Таблиця 7.3

Дані статистичних спостережень

Необхідно побудувати багатофакторну регресійну модель процесу переробки вагонів на металургійному комбінаті.