Тема 8. Квантовая физика атома. Постулаты Бора

Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся со временем) состояния, находясь в которых атом не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, на которых находятся электроны.

В стационарном состоянии атома для электрона, находящегося на круговой орбите, значения момента импульса могут принимать только определенный набор дискретных квантованных значений, удовлетворяющих условию:

( n = 1, 2, 3, …), где

m_e – масса электрона, υ_n – скорость электрона на n-ой орбите радиуса r_n,

n – номер орбиты,

ħ = (h – постоянная Планка).

Радиус n-ой орбиты для атома водорода:

,

где e – заряд электрона, ε_o – электрическая постоянная,

а– радиус первой орбиты (n = 1), называемыйпервым боровским радиусом, который равен:

.

Второй постулат Бора (правило частот): при переходе электрона с одной стационар­ной орбиты на другую излучается (или поглощается) один фотон с энергией hν, равной разности энергий соответствующих стационарных состояний E_n и Е_m :

.

При переходе атома из состояния большей энергии в состояние меньшей энергии, то есть при переходе электрона на менее удаленную от ядра орбиту, происходит излучение фотона, а при поглощении фотона происходит переход атома из состояния меньшей энергии в состояние большей энергии, что соответствует переходу электрона на более удаленную орбиту.

Дискретность набора значений энергии стационарных состояний E_n и Е_m предопределяет дискретность набора возможных частот ν квантовых переходов между этими состояниями, что обусловливает линейчатость спектра атома.

По теории Бора полная энергия электрона на n-ой орбите атома водорода:

( n = 1, 2 , 3, …),

Из приведенной формулы следует, что энергетические состояния атома водорода образуют после­довательность энергетических уровней, изменяющихся в зависимости от значения числа n , которое называетсяглавным квантовым числом.

Энергетическое состояние с n = 1 являетсяосновным состоянием, а состояния сn >1 являютсявозбужденными.

Спектр испускания атома водорода.

Согласно второму постулатуБора, при переходе атома водорода из состоянияn в состоя­ниет с меньшей энергией испускается фотон с энергиейhν :

,

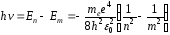откуда частота ν квантового перехода в спектре испускания атома водорода:

,

где R – постоянная Ридберга () ,

Числа m (m = 1, 2, 3 …) и n (n = m + 1, m + 2, m + 3, …) определяют номера электронных орбит в атоме, между которыми происходит квантовый переход.

Приведенная формула описывает серии линий в спектре испускания атома водорода (рис. 13), где m определяет серию (m = 1, 2, 3…), а n определяет отдельные линии соответствующей серии (n = m + 1, m + 2, m + 3, …).

Рис. 13.

В ультрафиолетовой области спектра атома водорода наблюдается

серия Лаймана (m = 1): (n = 2, 3, 4, …).

В видимой области спектра атома водорода наблюдается

серия Бальмера (m = 2): (n = 3, 4, 5, …).

В инфракрасной области спектра атома водорода наблюдаются

серия Пашена (m = 3): (n = 4, 5, 6, …);

серия Брэкета (m = 4): (n = 5, 6, 7, …);

серия Пфунда (m = 5): (n = 6, 7, 8, …);

серия Хэмфри (m = 6): 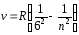(n = 7, 8, 9, …).

Квантовые числа и правила отбора.Состояние электрона в атоме водорода определяется набором квантовых чисел:n, l , m_l.

n – главное квантовое число, определяющее энергетические уровни электрона в атоме и принимающее целочисленные значения начиная от еди­ницы:

n= 1, 2 , 3, … .

l –орбитальное квантовое число, определяющее момент импульса электрона в атоме и для заданногоглавного квантового числа nпринимающее следующие значения: l = 0, 1, …, (n– 1), то есть всегоnзначений.

т_l –магнитное квантовое число,определяющее проекцию момента импульса электрона на заданное направление и при заданноморбитальном квантовом числе lпринимающее следующие значения:

т_l= 0, ±1, ±2, …, ±l,

то есть всего (2l+1) значений, причем вектор момента импульса электрона в атоме может иметь в пространстве (2l + 1) ориентацию.

Если орбитальное квантовыми число l = 0, то состояние электрона называютs-состоянием, дляl = 1 –p-состоянием, дляl = 2 –d-состоянием, дляl = 3 –f-состоянием и т. д. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в состояниях (n = 2,l = 0) и (n = 2,l = 1) обозначаются соответственно символами2s и2р.

Число возможных переходов электронов, связанных с испусканием или поглощением света, ограничено, так называемыми, правилами отбора.

Те­оретически доказано и экспериментально подтверждено, что могут осуществляться только такие переходы, для которых:

1) изменение орбитального квантового числа Dlудовлетворяет условию:

∆l = ±1 ;

2) изменение магнитного квантового числа Dm_l удовлетворяет условию:

∆m_l = 0, ±1 .

Учитывая число возможных состояний, соответствующих данному значению главного квантового числа nиправила отбора, спектральные линии атома водорода (рис. 14) в серии Лаймана соответствуют переходам: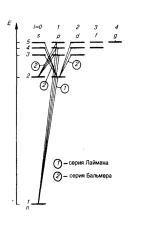

np →1s (n= 2, 3, …) ;

в серии Бальмера – переходам:

np →2s, ns →2p, nd →2p (n = 3, 4,…) и т. д.

Так как поглощающий атом находится обычно в основном состоянии, то спектр поглощения атома водорода состит из линий, соответствующих переходам: 1s→np

Рис. 14

(n = 2, 3, ...), что отражается в эксперименте.

S

α